
|
|
Определение момента инерции тела вращения
Цель работы: изучить характеристики и законы вращательного движения твёрдых тел. Приборы и принадлежности: тело вращения в подшипниках, набор грузов, секундомер, отсчетная линейка.
Теория метода и описание экспериментальной установки
Вращательным называется такое движение, при котором все точки твердого тела описывают окружности, центры которых лежат на одной и той же прямой, называемой осью вращения. Важнейшими характеристиками вращательного движения являются угловая скорость Угловой скоростью называется величина равная изменению угла поворота твердого тела за единицу времени, т. е.
Угловое ускорение описывает быстроту изменения угловой скорости;
При вращательном движении угловая скорость и угловое ускорение для всех частиц твердого тела одинаковы. Линейная скорость точки вращающегося тела связана с угловой скоростью соотношением:
где Для описания динамики вращательного движения понятий силы и массы недостаточно. Действительно, если при поступательном движении определенная сила вызывает вполне определенные изменения движения тела, то во вращательном движении результат действия силы зависит от того, на каком расстоянии от оси вращения она приложена. Произведение величины силы, приложенной к данной точке тела, на ее кратчайшее расстояние до оси вращения называется моментом силы
Произведение массы
Момент инерции всего тела равен сумме моментов инерции составляющих его материальных точек.
Момент инерции характеризует инертность тела во вращательном движении и, как видно из (6), зависит от характера распределения массы относительно оси вращения
Пусть твердое тело вращается под действием приложенной к нему силы
Эта работа идет на изменение кинетической энергии вращающегося тела, т. е.
Из равенства формул (8) и (9) следует
Величина
т.е. импульс момента силы равен изменению момента импульса вращающегося твердого тела. Это основной закон динамики вращательного движения. Закону можно придать и другую формулировку. Из (10) следует,
т.е. угловое ускорение, приобретаемое телом под действием вращающегося момента Экспериментальная установка представляет собой маховик, насажанный на вал, который может вращаться на шарикоподшипниках вокруг горизонтальной оси. На стене лаборатории вертикально закреплена измерительная линейка. На вал намотана нить, к концу которой прикреплен груз массой
Рисунок 4. Установка для определения момента инерции маховика.
Закон сохранения энергии для рассматриваемой системы запишется следующим образом:
где
Считаем, что сила трения постоянна. Тогда
Так как движение груза
где
где Подставляя в (13) соотношения (14), (15) и (16) и учитывая, что
Таким образом, для определения момента инерции тела вращения необходимо измерить время
Измерения и обработка их результатов
1. Взвесьте груз с помощью технических весов. 2. Измерьте штангенциркулем диаметр вала 3. При полностью размотанном шнуре отметьте по шкале наименьшую координату платформы 4. Намотайте шнур на вал и отметьте наибольшую координату 5. Придерживая маховик, поставьте на платформу груз и отпустите маховик, включив секундомер в момент начала движения системы. В момент, когда шнур полностью размотается, выключите секундомер и снимите показание времени 6. Отметьте по шкале максимальную координату 7. Опыт повторите 3 раза при различных массах груза и результаты измерений занесите в таблицу 5. 8. По формуле (17) вычислите момент инерции
Таблица 5.– Результаты измерений и вычислений
9. Окончательный результат представьте в виде.
Контрольные вопросы
1. Что называется моментом инерции тела, и каков его физический смысл? 2. Выведите формулу кинетической энергии вращающегося тела. 3. Как рассчитывается кинетическая энергия тела, одновременно участвующего в поступательном и вращательном движении? 4. Выведите формулу основного уравнения динамики вращательного движения твердого тела. 5. Исходя из закона сохранения энергии, выведите расчетную формулу для момента инерции махового колеса без учета сил трения. 6. Оцените момент инерции установки данной работы, не прибегая к опыту.
Лабораторная работа № 5
Определение ускорения свободного падения с помощью оборотногомаятника
Цель работы: 1. Изучить гармоническое колебательное движение на примере малых колебаний физического маятника. 2. Определить ускорение свободного падения методом оборотного маятника. Приборы и принадлежности:оборотный физический маятник, секундомер.
Теория метода и описание экспериментальной установки
Периодические смещения тела относительно некоторого устойчивого положения (положения равновесия) называют колебательным движением или просто колебаниями. Колебательные движения в общем случае представляют собой, сложные физические процессы. Учение о колебаниях служит основой целого ряда прикладных дисциплин (акустика, теория машин и механизмов, сейсмология и др.). Простейшим видом колебаний является гармоническое колебательное движение. Гармонические колебания тела возникают при действии силы
Эту силу называют возвращающей. Природа возвращающей силы может быть различной (сила упругости, сила тяжести и др.). При гармоническом колебательном движении зависимость смещения
где Ускорение
Гармонические колебания совершают маятники под действием силы тяжести при малых углах отклонения от положения равновесия. Твердое тело произвольной формы, способное совершать малые колебания около положения равновесия, представляет собой физический маятник (например, тело, подвешенное в точке, не совпадающей с центром тяжести). Всякое твердое тело можно рассматривать как совокупность материальных точек с массами
где Момент
Рисунок 5. Физический маятник.
Под действием момента силы тяжести маятник совершает колебания, при этом центр тяжести движется по дуге окружности с угловым ускорением
а по второму закону Ньютона уравнение вращательного движения запишется:
где Подставив в уравнение (4) значение
Уравнение (5) отличается от уравнения (2) только тем, что в него входят угловые величины вместо линейных. Из сравнения уравнений (2) и (5) следует, что
откуда для периода колебаний физического маятника имеем:
Во всяком физическом маятнике можно найти такие две точки, при последовательном подвешивании за которые период маятника остается неизменным. Расстояние между этими точками называется приведённой длиной По теореме Штейнера момент инерции маятника
где Из формул (6) и (7) имеем
Пусть в данном оборотном маятнике мы нашли два таких положения оси подвеса, что периоды колебаний относительно их одинаковы. Тогда на основании формулы (8) можно записать
где
Так как оси расположены на различных расстояниях от центра инерции, т.е.
Величина периодами является приведенной длиной Оборотный маятник (рис.6.) состоит из стержня с нониусом 1, чечевицы подвижной 2 и неподвижной 3, опорных призм 4 и 5, Маятник одной из опорных призм устанавливается на подушке кронштейна, прикрепленного к стене. Расстояние между призмами 4 и 5 постоянное и равно
Рисунок 6. Оборотный маятник.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 и угловое ускорение
и угловое ускорение  .
. (1)
(1) (2)
(2) , (3)
, (3) расстояние точки от оси вращения. Из этой формулы видно, что линейные скорости различных точек различны.
расстояние точки от оси вращения. Из этой формулы видно, что линейные скорости различных точек различны. . (4)
. (4) - ой материальной точки на квадрат расстояния се до оси вращения называется моментом инерции материальной точки
- ой материальной точки на квадрат расстояния се до оси вращения называется моментом инерции материальной точки . (5)
. (5) . (6)
. (6) . По аналогии с поступательным движением, кинетическая энергия вращающегося тела равна:
. По аналогии с поступательным движением, кинетическая энергия вращающегося тела равна: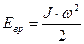 . (7)
. (7) . Рассмотрим достаточно малый промежуток времени
. Рассмотрим достаточно малый промежуток времени  , такой, чтобы угловую скорость можно было считать постоянной. Тогда за время
, такой, чтобы угловую скорость можно было считать постоянной. Тогда за время  тело повернется с угловой скоростью
тело повернется с угловой скоростью  . При этом точка приложения силы описывает дугу
. При этом точка приложения силы описывает дугу  . Элементарная работа в этом случае равна:
. Элементарная работа в этом случае равна: (8)
(8) . (9)
. (9) ,
, или
или  . (10)
. (10) называется моментом импульса (или моментом количества движения). Произведение
называется моментом импульса (или моментом количества движения). Произведение 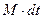 называется импульсом вращающегося момента силы. Последнее выражение можно переписать в виде:
называется импульсом вращающегося момента силы. Последнее выражение можно переписать в виде: , (11)
, (11) или
или  , (12)
, (12)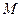 прямо пропорционально величине этого момента и обратно пропорционально моменту инерции тела
прямо пропорционально величине этого момента и обратно пропорционально моменту инерции тела  относительно оси вращения.
относительно оси вращения.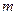 . Груз под действием силы тяжести будет опускаться, приводя во вращение маховик. Поскольку груз и маховик связаны нитью, то после того, как груз опустится на полную длину нити
. Груз под действием силы тяжести будет опускаться, приводя во вращение маховик. Поскольку груз и маховик связаны нитью, то после того, как груз опустится на полную длину нити  , маховик, вращаясь по инерции, поднимет груз снова на какую-то высоту
, маховик, вращаясь по инерции, поднимет груз снова на какую-то высоту  , (рис.4) меньшую
, (рис.4) меньшую  .
.
 , (13)
, (13) кинетическая энергия поступательного движения,
кинетическая энергия поступательного движения,  кинетическая энергия вращательного движения,
кинетическая энергия вращательного движения,  работа по преодолению сил трения
работа по преодолению сил трения 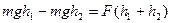 .
.
 . (14)
. (14) , (15)
, (15) время опускания груза от
время опускания груза от 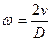 , (16)
, (16) диаметр вала.
диаметр вала. , получаем:
, получаем: . (17)
. (17) .
. .
. . Очевидно,
. Очевидно,  .
.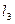 подъема груза и определите высоту
подъема груза и определите высоту  .
. и среднюю абсолютную погрешность
и среднюю абсолютную погрешность  .
. и направленной противоположно смещению т.е.
и направленной противоположно смещению т.е. .
. , (1)
, (1)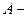 амплитуда колебаний (максимальное смещение колеблющейся точки от среднего положения);
амплитуда колебаний (максимальное смещение колеблющейся точки от среднего положения);  круговая (циклическая) частота;
круговая (циклическая) частота; 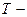 период колебаний (время одного полного колебания);
период колебаний (время одного полного колебания);  начальная фаза колебания.
начальная фаза колебания.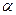 тела, совершающего гармонические колебания, пропорционально смещению и направлено противоположно смещению:
тела, совершающего гармонические колебания, пропорционально смещению и направлено противоположно смещению: . (2)
. (2) и т.д. При отклонении физического маятника от положения равновесия на угол
и т.д. При отклонении физического маятника от положения равновесия на угол  (рис.5.) на каждый его элемент будет действовать момент силы тяжести относительно оси вращения
(рис.5.) на каждый его элемент будет действовать момент силы тяжести относительно оси вращения  . Сумма моментов всех этих сил равна моменту равнодействующей силы тяжести
. Сумма моментов всех этих сил равна моменту равнодействующей силы тяжести  , приложенной к центру тяжести маятника (точка
, приложенной к центру тяжести маятника (точка  ) относительно оси вращения Величина момента
) относительно оси вращения Величина момента ,
,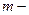 масса маятника;
масса маятника; 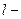 расстояние от оси вращения
расстояние от оси вращения 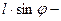 плечо силы тяжести
плечо силы тяжести  ускорение силы тяжести в данном месте.
ускорение силы тяжести в данном месте. . (3)
. (3)
 или
или  , (4)
, (4)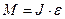
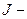 момент инерции маятника относительно оси вращения.
момент инерции маятника относительно оси вращения. . (5)
. (5) , или
, или  ,
, (6)
(6)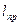 данного маятника.
данного маятника. , (7)
, (7) момент инерции относительно оси, параллельной оси вращения и проходящей через центр инерции маятника.
момент инерции относительно оси, параллельной оси вращения и проходящей через центр инерции маятника. . (8)
. (8)
 расстояния от центра инерции оборотного маятника до обеих осей. Выразим из каждой формулы для
расстояния от центра инерции оборотного маятника до обеих осей. Выразим из каждой формулы для  величины
величины  и приравняем полученные выражения. После преобразования получим
и приравняем полученные выражения. После преобразования получим
 то можно сократить
то можно сократить  и получить
и получить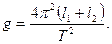
 , равная расстоянию между осями маятника с одинаковыми
, равная расстоянию между осями маятника с одинаковыми .
.