
|
|
Рассмотрим энергию переносимую упругой волнойx распространяющейся вдоль оси OX. Для элементарного объема среды ∆ Кинетическая энергия объема ∆
где r – плотность среды, ∆m = r∆v. Потенциальная энергия является энергией деформированного объема ∆ В качестве примера рассмотрим энергию упругой деформации стержня. При растяжении (сжатии) его относительное удлинение равно:
Однородные стержни ведут себя при растяжении или сжатии подобно пружине. Экспериментально установлено, что для стержней из данного материала относительное удлинение при упругой деформации пропорционально силе, приходящейся на единицу площади поперечного сечения стержня:
(a – коэффициент пропорциональности). Величина, равная отношению силы к величине поверхности, на которую действует сила, называется напряжением. Отношение
Для характеристики упругих свойств материалов пользуются величиной
из которого следует, что модуль Юнга равен такому нормальному напряжению (если сила направлена по нормали к поверхности), при котором относительное удлинение было бы равно единице (т.е. приращение длины ∆l было бы равно первоначальной длине lo). Решив уравнение (37.4) относительно F и заменив ε через
где k – постоянный для данного стержня коэффициент. Соотношение (37.7) выражает закон Гука для стержня ( Как известно, работа, которую нужно совершить, чтобы вызвать удлинение x пружины, определяется соотношением:
Аналогично найдем выражение для работы, совершаемой при упругом растяжении или сжатии стержня. В соответствии с формулой (37.7) эта работа равна:
где ∆ Работа при упругой деформации равна потенциальной энергии упругого деформированного стержня:
При распространении продольной плоской волны в среде объем сечением S и длиной ∆х, т.е. ∆
(символ частной производной Следует отметить, что относительная деформация
Там, где отклонения частиц от положения равновесия максимальны, деформация и напряжение равны нулю (рис. 37.1), в местах, где частицы проходят через положение равновесия (x = 0) деформация и напряжение достигают максимального значения, причем, положительные и отрицательные деформации (т.е. растяжения и сжатия) чередуются друг с другом. В соответствии с этим продольная волна состоит из чередующихся разрежений и сгущений среды. С учетом соотношений (37.10) и (37.11) деформированный объем среды ∆
Для фазовой скорости с продольных упругих волн имеется экспериментально проверенное соотношение:
где Е – модуль Юнга, r – плотность среды. С учетом формулы (37.14) соотношение (37.13) примет вид:
Выражение (37.2) и (37.15) в сумме дают полную энергию
Разделив эту энергию на объем ∆
Дифференцирование уравнения (37.1) один раз по t, другой раз по х дает
Подставив эти выражения в формулу (37.17) и приняв во внимание, что k2c2 =w2 получим
Из (37.18) следует, что плотность энергии в каждый момент времени в разных точках пространства различна. В одной и той же точке плотность энергии изменяется со временем по закону квадрата синуса. Среднее значение квадрата синуса равно
Зависимости плотности энергии (37.18) и ее среднего значения (37.19) имеют место не только для незатухающей плоской волны, но и для других видов волн( плоской затухающей, сферической и т.д.). Итак, среда, в которой распространяется волна, обладает дополнительным запасом энергии. Эта энергия доставляется от источника колебаний в различные точки среды самой волной; следовательно волна переносит с собой энергию. Потоком энергии, переносимой волной через некоторую поверхность, называется количество энергии через эту поверхность в единицу времени. Поток энергии совпадает с размерностью мощности. Для характеристики течения энергии в разных точках пространства вводится векторная величина, называемая плотностью потока энергии. Направление вектора плотности потока энергии совпадает с направлением переноса энергии. Если через площадку ∆S^, перпендикулярную к направлению распространения волны, переносится за ∆t энергия ∆W, то плотность потока энергии
Через площадку ∆S^ будет переноситься энергия, заключенная в объеме∆
Подставить это выражение в формулу (37.20), получим для плотности потока энергию
Введя вектор
Мы получили выражение для вектора плотности потока энергии. Этот вектор называется вектором Умова. Вектор (37.23), как и плотность энергии w, различен (см.(37.18)) в разных точках пространства, а в данной точке изменяется со временем по закону квадрата синуса. Его среднее значение равно:
(см. (37.19)). Выражение (37.24), так же как и (37.19) справедливо для волны любого вида (сферической, затухающей и т.д.). Интенсивностью волны I называется модуль среднего значения вектора Умова. Интенсивность волны численно равна энергии, переносимой волной за единицу времени сквозь единицу площади поверхности, нормальной к направлению распространения волны. Для плоской и сферической синусоидальных волн

Зная равен dV = c × dt × dS cosj. В нем содержится энергия dW = w dV = w с dt dS cosj (w – мгновенное значение плотности энергии в том месте, где расположена площадка dS). Приняв во внимание, что
Полный поток энергии через поверхность S равен сумме элементарных потоков (37.26):
т.е. поток энергии равен потоку вектора
ГЛАВА 38 Вопросы: 1. Звуковые волны. Характеристика звука интенсивность, частота акустические спектры. 2. Громкость, уровень громкости. Единица измерения громкости – бел. 3. Эффект Доплера для звуковых волн.
Упругие волны, распространяющиеся в любой среде, имеющие частоты от 16 до 20000 Гц, называются звуковыми волнами или просто звуком, а учение о звуках называется акустикой. Упругие волны с частотами меньшими 16 Гц, называют инфразвуком. Волны с частотами, превышающими 20000 Гц, называют ультразвуком. Всякий реальный звук является наложением гармонических колебаний с определённым набором частот, который называется акустическим спектром звука. Если в звуке присутствуют колебания всех частот в некотором спектральном интервале от Высота тонального звука определятся основной (наименьшей) частотой. Относительная интенсивность обертонов (т.е. колебаний с частотами Под интенсивностью звука понимают среднее по времени значение плотности потока энергии, которое несёт с собой звуковая волна (см. 37.25 главы 37)
где Для того чтобы вызвать звуковое ощущение, волна должна обладать некоторой минимальной интенсивностью, которая называется порогом слышимости. Порог слышимости несколько различен для разных лиц и сильно зависит от частоты звука, Наиболее чувствительно человеческое ухо к частотам от 1000 до 4000 Гц. В этой области частот порог слышимости составляет в среднем около
Громкость звука, оцениваемая субъективно, возрастает гораздо медленнее, чем интенсивность звуковых волн. При возрастании интенсивности в геометрической прогрессии громкость возрастает приблизительно в арифметической прогрессии, т.е. линейно. На этом основании уровень громкости L определяется как логарифм отношения интенсивности данного звука I к интенсивности I0, принятой за исходную:
Исходная интенсивность I0 принимается равной 10-12 Вт/м2, так что порог слышимости при частоте порядка 1000 Гц лежит на нулевом уровне (L = 0). Единица уровня громкости L, определяемого формулой (38.2), называется белом (Б). Однако обычно пользуются в 10 раз меньшими единицами – децибелами (дБ). Значение Lв децибелах определяется формулой
Отношение двух интенсивностей I1 и I2 (например, при сравнении интенсивностей от двух источников излучения) также может быть выражено в децибелах:
Весь диапазон интенсивностей, при которых волна вызывает в человеческом ухе звуковое ощущение (от 10-12 до 10Вт/м2), соответствует значениям уровня громкости от 0 до 130дБ. Энергия, которую несут с собой звуковые волны, крайне мала. Произведём расчёт интенсивности звуковой волны, при уровне громкости L=60дБ (речь средней громкости). Воспользуемся формулой (38.3)
Расчёт интенсивности звуковой волны по формуле (38.1) даёт следующий результат. При громкости 60 дБ амплитуда А колебаний частиц составляет ~4∙10-7 м для самых длинных волн =16 Гц и ~3∙10 -10м для самых коротких ( Плотность воздуха
Расчёт по (38.1) даёт следующие результаты: для Уникальные свойства звуковых волн и в особенности ультразвука позволяют использовать его во многих областях науки и техники, в методах научных исследований и в способах воздействия на вещество. Перечислим лишь некоторые из областей применения ультразвука: ускорение различных технологических процессов, влияние на скорость протекания химических реакций, разрушение плёнок оксидов (пайка алюминия), удаление нагара и накипи в котлах, обезжиривание поверхностей деталей, обработка и резание твёрдых и хрупких материалов, влияние на качество отливок, стерилизация жидкостей и т.д. Остановимся на некоторых особенностях регистрации звуковых волн. Если источник, излучающий звуковые волны с частотой Сначала рассмотрим случай, когда источник звука приближается со скоростью За время, равное периоду колебаний
Если источник удаляется от приёмника со скоростью
Поскольку частота воспринимаемого приемником звука определяется соотношением
Здесь знак «плюс» соответствует удалению источника от приёмника, знак «минус» – приближению к нему.
В случае если приёмник приближается к неподвижному источнику со скоростью
При удалении приёмника в формуле (38.8) вместо знака плюс появится знак минус, и мы сможем записать:
Для обоих случаев (объединив соотношения (38.8) и (38.9)) получаем:
Если источник и приёмник перемещаются одновременно вдоль соединяющей их прямой, то, объединив уравнения (38.7) и (38.10) получим выражение для частоты
В самом общем случае, когда и приемник, и источник звуковых волн движутся относительно среды с произвольными скоростями, направления которых не совпадают с проходящей через источник и приёмник прямой (рис. 38.3. б), в формуле (38.11) вместо значений
При этом верхние знаки перед скоростями

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , (37.1)
, (37.1) скорость движения частиц среды Vчаст и деформацию среды ε во всех точках этого объема можно считать одинаковыми и равными соответственно
скорость движения частиц среды Vчаст и деформацию среды ε во всех точках этого объема можно считать одинаковыми и равными соответственно  и
и 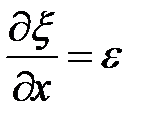

 (37.2)
(37.2) (37.3)
(37.3)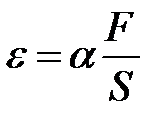 (37.4)
(37.4) – напряжение. Следовательно, формуле (37.4) можно придать вид:
– напряжение. Следовательно, формуле (37.4) можно придать вид: (37.5)
(37.5) , которая называется модулем Юнга. Эта величина измеряется в паскалях (1Па=1Н/1м2). Таким образом соотношение (37.5) можно записать в виде:
, которая называется модулем Юнга. Эта величина измеряется в паскалях (1Па=1Н/1м2). Таким образом соотношение (37.5) можно записать в виде: , (37.6)
, (37.6) , а a через
, а a через  , получим формулу:
, получим формулу: , (37.7)
, (37.7) , знак «минус» указывает, что проекция упругой силы на ось ОХ и координата Х всегда имеют разные знаки).
, знак «минус» указывает, что проекция упругой силы на ось ОХ и координата Х всегда имеют разные знаки). (37.8)
(37.8) ,(37.9)
,(37.9) – относительное удлинение (см. (37.3)).
– относительное удлинение (см. (37.3)). . (37.10)
. (37.10) (
(  – растяжению), или относительное удлинение
– растяжению), или относительное удлинение  меняется с изменением х не по линейному закону, истинная деформация в разных сечениях х будет неодинаковой. Чтобы получить деформацию ε в сечении х, нужно устремить ∆х к нулю. Таким образом,
меняется с изменением х не по линейному закону, истинная деформация в разных сечениях х будет неодинаковой. Чтобы получить деформацию ε в сечении х, нужно устремить ∆х к нулю. Таким образом, , (37.11)
, (37.11) взят потому, что
взят потому, что  (37.12)
(37.12)






 (37.13)
(37.13) , (37.14)
, (37.14) (37.15)
(37.15) (37.16)
(37.16) (37.17)
(37.17)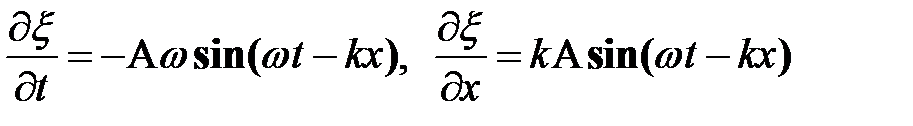
 (37.18)
(37.18) . Соответственно, среднее по времени значение плотности энергии в каждой точке среды равно
. Соответственно, среднее по времени значение плотности энергии в каждой точке среды равно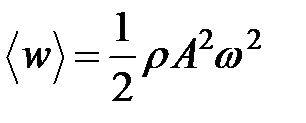 (37.19)
(37.19)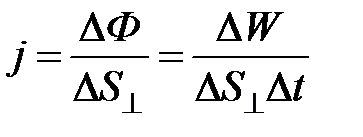 (37.20)
(37.20) (37.21)
(37.21) (37.22)
(37.22) , модуль которого равен фазовой скорости волны, а направление совпадает с направлением распространения волны (и переноса энергии), получим:
, модуль которого равен фазовой скорости волны, а направление совпадает с направлением распространения волны (и переноса энергии), получим: (37.23)
(37.23) (37.24)
(37.24) (37.25)
(37.25) во всех точках произвольной поверхности S , можно вычислить поток энергии через эту поверхность. С этой целью разобьем поверхность на элементарные участки dS. За время dt через площадку dS пройдет энергия dW, заключенная в косом цилиндре (рис. 37.2). Объём этого цилиндра
во всех точках произвольной поверхности S , можно вычислить поток энергии через эту поверхность. С этой целью разобьем поверхность на элементарные участки dS. За время dt через площадку dS пройдет энергия dW, заключенная в косом цилиндре (рис. 37.2). Объём этого цилиндра
 , можно написать:
, можно написать:  . Отсюда для потока энергии
. Отсюда для потока энергии  через площадку dS получаем соотношение
через площадку dS получаем соотношение (37.26)
(37.26) , (37.27)
, (37.27)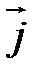 через поверхность S. Среднее значение потока Ф равно:
через поверхность S. Среднее значение потока Ф равно: (37.28)
(37.28) до
до  , то спектр называется сплошным. Если звук состоит из колебаний дискретных частот
, то спектр называется сплошным. Если звук состоит из колебаний дискретных частот  ,
,  ,
,  и т.д., то спектр называется линейчатым. Сплошным акустическим спектром обладают шумы. Линейчатым спектром обладают звуки, издаваемые музыкальными инструментами. Колебания с линейчатым спектром вызывают ощущение звука с более или менее определённой высотой. Такой звук называется тональным.
и т.д., то спектр называется линейчатым. Сплошным акустическим спектром обладают шумы. Линейчатым спектром обладают звуки, издаваемые музыкальными инструментами. Колебания с линейчатым спектром вызывают ощущение звука с более или менее определённой высотой. Такой звук называется тональным. , (38.1)
, (38.1) – средняя плотность энергии волны, с – фазовая скорость,
– средняя плотность энергии волны, с – фазовая скорость,  – плотность среды, А – амплитуда,
– плотность среды, А – амплитуда, 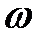 – циклическая частота звуковой волны.
– циклическая частота звуковой волны. Вт/м2. При других частотах порог слышимости лежит выше (смотреть нижнюю кривую 1 на рис. 38.1).
Вт/м2. При других частотах порог слышимости лежит выше (смотреть нижнюю кривую 1 на рис. 38.1).













 (38.2)
(38.2) (38.3)
(38.3) (38.4)
(38.4)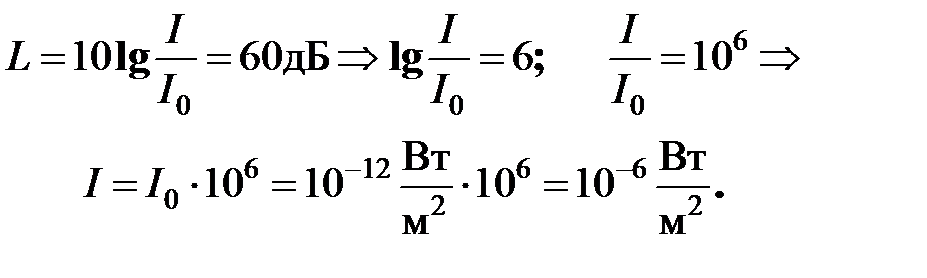
 Гц) волн; скорость распространения звуковых волн в воздухе
Гц) волн; скорость распространения звуковых волн в воздухе 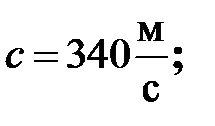

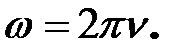
 для
для  16 Гц
16 Гц 20000Гц
20000Гц 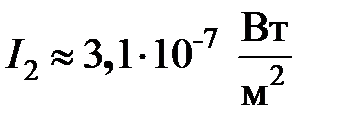
 , и приемник звука неподвижны относительно среды, в которой распространяются волны, то частоты колебаний
, и приемник звука неподвижны относительно среды, в которой распространяются волны, то частоты колебаний  , воспринимаемых приёмником будет равна частоте
, воспринимаемых приёмником будет равна частоте  колебаний источника
колебаний источника  . Если источник или приёмник звука перемещается относительно среды, то частота
. Если источник или приёмник звука перемещается относительно среды, то частота  к неподвижному наблюдателю (приёмнику). Фазовая скорость cзвукав среде полностью определятся её упругими и инерционными свойствами и не зависит от состояния движущегося или покоящегося источника. Поэтому относительно среды скорость волны всегда равна c.
к неподвижному наблюдателю (приёмнику). Фазовая скорость cзвукав среде полностью определятся её упругими и инерционными свойствами и не зависит от состояния движущегося или покоящегося источника. Поэтому относительно среды скорость волны всегда равна c. , источник приблизится к приёмнику на расстояние,
, источник приблизится к приёмнику на расстояние,  ,
, 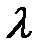 волны (рис. 38.2 а), распространяющейся в направлении движения источника, будет меньше, чем
волны (рис. 38.2 а), распространяющейся в направлении движения источника, будет меньше, чем  , на величину
, на величину  :
: (38.5)
(38.5)





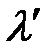


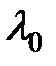



 (рис. 38.2 б), то длина волны
(рис. 38.2 б), то длина волны  , распространяющейся в среде в направлении неподвижного приёмника, будет больше, чем
, распространяющейся в среде в направлении неподвижного приёмника, будет больше, чем  (38.6)
(38.6) , то для обоих случаев (соотношения (38.5) и (38.6) можем записать
, то для обоих случаев (соотношения (38.5) и (38.6) можем записать (38.7)
(38.7)



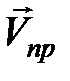
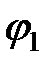
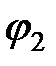

 (рис. 38.3. а), скорость звука относительно приёмника увеличится в соответствии с теоремой сложения скоростей и станет по величине равной
(рис. 38.3. а), скорость звука относительно приёмника увеличится в соответствии с теоремой сложения скоростей и станет по величине равной  . Длина волны от неподвижного источника
. Длина волны от неподвижного источника  . Тогда
. Тогда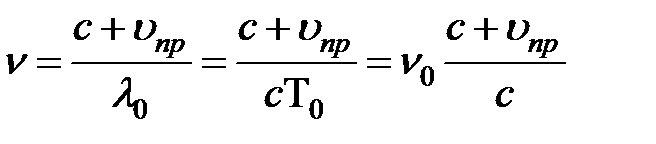 (38.8)
(38.8) (38.9)
(38.9) (38.10)
(38.10) (38.11)
(38.11) и
и  на направление указанной прямой. В этом случае формула (38.11) примет вид:
на направление указанной прямой. В этом случае формула (38.11) примет вид: (38.12)
(38.12)