Затухающие колебания. Дифференциальное уравнение
ГЛАВА 32
Вопросы:
Гармонические колебания и их характеристики
Дифференциальное уравнение гармонических колебаний
И его решение
Пружинный, физический и математический маятники
Гармонический осциллятор
Колебаниями называются процессы, в той или иной степени повторяющиеся во времени.
К механическим колебаниям относятся колебания маятников, струн, частей машин и механизмов, зданий, мостов и других сооружений, качка корабля, волнение моря и т.п.
Система, совершающая колебания, называется колебательной системой.
Свободными (собственными) колебаниями называются колебания, которые происходят в отсутствие переменных внешних воздействий на колебательную систему и возникают вследствие какого-либо начального отклонения этой системы от состояния ее устойчивого равновесия.
Вынужденными колебаниями называют колебания, возникающие в какой-либо системе под влиянием переменного внешнего воздействия (например, колебания силы тока в электрической цепи, вызываемые переменной ЭДС; колебания маятника, вызываемые переменной внешней силой).
Колебания называют периодическими, если значения всех физических величин, характеризующих колебательную систему и изменяющихся при ее колебаниях, повторяются через равные промежутки времени. Наименьший промежуток времени 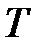 , удовлетворяющий этому условию, называется периодом колебаний. За период колебаний , удовлетворяющий этому условию, называется периодом колебаний. За период колебаний 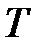 система совершает одно полное колебание. Частотой периодических колебаний называется величина система совершает одно полное колебание. Частотой периодических колебаний называется величина  , равная числу полных колебаний, совершающихся за единицу времени. Циклической, или круговой, частотой периодических колебаний называется величина , равная числу полных колебаний, совершающихся за единицу времени. Циклической, или круговой, частотой периодических колебаний называется величина  , равная числу полных колебаний, совершающихся за , равная числу полных колебаний, совершающихся за  единиц времени. единиц времени.
При периодических колебаниях зависимость колеблющейся величины  от времени от времени  удовлетворяет условию удовлетворяет условию  . .
Периодические колебания величины 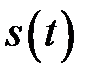 называются гармоническими колебаниями, если физическая величина изменяется во времени по синусоидальному или косинусоидальному закону, то есть называются гармоническими колебаниями, если физическая величина изменяется во времени по синусоидальному или косинусоидальному закону, то есть
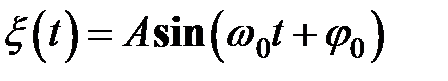 или или
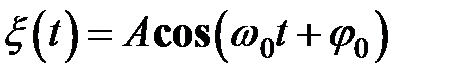 , (32.1) , (32.1)
где  – циклическая, или круговая, частота гармонических колебаний, – циклическая, или круговая, частота гармонических колебаний,  – максимальное значение колеблющейся величины – максимальное значение колеблющейся величины  , называемое амплитудой колебаний, , называемое амплитудой колебаний,  и и  постоянные величины. Значение постоянные величины. Значение  в произвольный момент времени в произвольный момент времени  определяется значением фазы колебаний определяется значением фазы колебаний  (соответственно (соответственно  ). Величины ). Величины  и и  представляют собой начальные фазы колебаний, то есть значение представляют собой начальные фазы колебаний, то есть значение  и и  в момент ( в момент (  ) начала отсчета времени ) начала отсчета времени 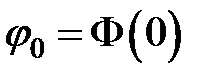 , ,  . .
Если материальная точка совершает свободные прямолинейные гармонические колебания вдоль оси координат  около положения равновесия, принятого за начало координат, то зависимость координаты около положения равновесия, принятого за начало координат, то зависимость координаты  точки от времени точки от времени  имеет вид имеет вид
 . (32.2) . (32.2)
Проекции скорости  и ускорения и ускорения  точки на ось точки на ось  равны равны
 , ,
 , (32.3) , (32.3)
где  – амплитуда скорости, – амплитуда скорости,  – амплитуда ускорения. – амплитуда ускорения.
Сила  , действующая на материальную точку, равна , действующая на материальную точку, равна  и и
 , (32.4) , (32.4)
где  – масса материальной точки. Следовательно, сила – масса материальной точки. Следовательно, сила  пропорциональна смещению материальной точки из положения равновесия и стремится вернуть точку в положение равновесия. пропорциональна смещению материальной точки из положения равновесия и стремится вернуть точку в положение равновесия.
 , (32.5) , (32.5)
где  – орт оси – орт оси  . Здесь . Здесь 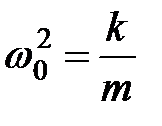 . .
Такая зависимость силы от смещения характерна, например, для упругой силы
 . (32.6) . (32.6)
Здесь  – вектор перемещения упруго деформированного тела при его продольном растяжении или сжатии, – вектор перемещения упруго деформированного тела при его продольном растяжении или сжатии,  – коэффициент упругости. – коэффициент упругости.
Поэтому силы иной физической природы, удовлетворяющие тому же виду зависимости, называются квазиупругими силами или возвращающими силами.
Материальная точка, колеблющаяся под действием квазиупругой (возвращающей) силы (32.6) называется линейным гармоническим осциллятором. Ее динамическое поведение описывается дифференциальным уравнением  или или
 + +  , (32.7) , (32.7)
(здесь 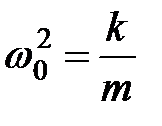 ), общее решение которого – уравнение (32.2). ), общее решение которого – уравнение (32.2).
Рассмотрим несколько простейших систем с одной степенью свободы, совершающих свободные гармонические колебания.
Пример 1
Рассмотрим движение пружинного маятника, который представляет собой материальную точку массой  , подвешенную на пружине жесткостью , подвешенную на пружине жесткостью  (рис. 32.1). Такая система представляет собой линейный гармонический осциллятор. В произвольном положении (рис. 32.1). Такая система представляет собой линейный гармонический осциллятор. В произвольном положении  на точку действует сила тяжести на точку действует сила тяжести  , сила упругости , сила упругости  , где , где  ст– статическая деформация в состоянии равновесия. ст– статическая деформация в состоянии равновесия.
На основании второго закона Ньютона запишем дифференциальное уравнение движения в проекции на ось  (начало координат совмещено с положением статического равновесия, в котором сила тяжести (начало координат совмещено с положением статического равновесия, в котором сила тяжести  уравновешивается силой упругости, равной уравновешивается силой упругости, равной  ): ):
 . (32.8) . (32.8)
m 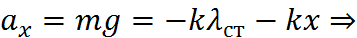
Из сравнения с уравнением (32.7) следует, что колебания пружинного маятника происходит по закону  , где , где  , амплитуда , амплитуда  и начальная фаза и начальная фаза  определяются с помощью начальных условий (по значениям координаты определяются с помощью начальных условий (по значениям координаты  и скорости и скорости  в начальный момент времени в начальный момент времени  ). Период колебаний ). Период колебаний  определяется соотношением определяется соотношением  . .
Пример 2
Математический маятник – материальная точка, подвешенная на невесомой нерастяжимой длиной нити и совершающая малые колебания в вертикальной плоскости под действием силы тяжести и силы упругости нити (рис. 32.2).
Составим дифференциальное уравнение движения математического маятника. Второй закон Ньютона в проекции на касательную 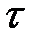 имеет вид: имеет вид:
  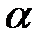  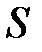      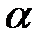  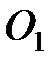 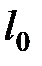    
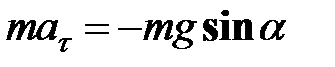 . (32.9) . (32.9)
В случае малых отклонений от положения равновесия, когда 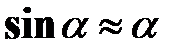 , получим дифференциальное уравнение осциллятора , получим дифференциальное уравнение осциллятора 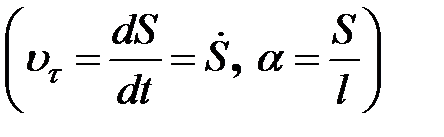 : :
 , ,
 . (32.10) . (32.10)
Следует отметить, что в данном случае точка массой  движется по дуге окружности под действием касательной составляющей движется по дуге окружности под действием касательной составляющей  . В случае малых колебаний сила . В случае малых колебаний сила 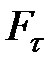 оказывается пропорциональной длине дуги оказывается пропорциональной длине дуги 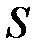  , то есть совпадает по виду с упругой силой , то есть совпадает по виду с упругой силой  в законе Гука и потому называется квазиупругой силой. Таким образом, причиной появления возвращающей силы в системе могут быть не только силы упругости, но и другие силы, например, сила тяжести при наличии связи в виде нити длиной в законе Гука и потому называется квазиупругой силой. Таким образом, причиной появления возвращающей силы в системе могут быть не только силы упругости, но и другие силы, например, сила тяжести при наличии связи в виде нити длиной  в случае математического маятника. в случае математического маятника.
Пример 3
Физический маятник – твердое тело, имеющее возможность качаться под действием его силы тяжести  вокруг неподвижной горизонтальной оси вокруг неподвижной горизонтальной оси  , не проходящей через центр тяжести тела (рис. 32.3) и называемой осью качания маятника (а также под действием реакции опоры оси , не проходящей через центр тяжести тела (рис. 32.3) и называемой осью качания маятника (а также под действием реакции опоры оси  ). Центр тяжести маятника совпадает с его центром инерции ). Центр тяжести маятника совпадает с его центром инерции  . Точка . Точка  пересечения оси качания маятника с вертикальной плоскостью, проходящей через центр тяжести маятника и перпендикулярной к оси качания, называется точкой подвеса маятника. пересечения оси качания маятника с вертикальной плоскостью, проходящей через центр тяжести маятника и перпендикулярной к оси качания, называется точкой подвеса маятника.
Поскольку мы имеем дело с вращательным движением тела, воспользуемся основным уравнением динамики вращательного движения относительно горизонтальной оси вращения (ось проходит через точку  перпендикулярно к плоскости рис. 32.3): перпендикулярно к плоскости рис. 32.3):
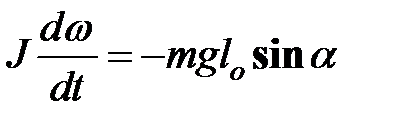 , ,
где  – момент инерции маятника относительно оси вращения. – момент инерции маятника относительно оси вращения.
В случае малых колебаний  получим уравнение осциллятора для вращательного движения получим уравнение осциллятора для вращательного движения  : :
 (32.11) (32.11)
Решение этого уравнения имеет вид:
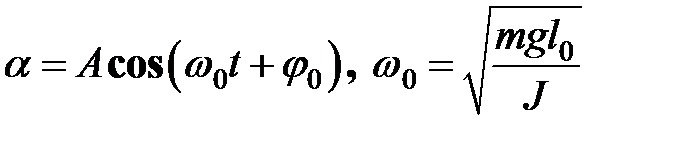 . (32.12) . (32.12)
Из полученного решения следует, что при малых отклонениях от положения равновесия физический маятник совершает свободные гармоническое колебания (в отсутствие трения) с циклической частотой 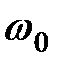 , периодом , периодом
 (32.13) (32.13)
и амплитудой колебания  ( (  – максимальный угол поворота маятника вокруг оси вращения от положения равновесия). – максимальный угол поворота маятника вокруг оси вращения от положения равновесия).
Введем понятие приведенной длины физического маятника, определив ее как длину  такого математического маятника, который совершает колебания с той же частотой, что и физический маятник. Приравняв частоты такого математического маятника, который совершает колебания с той же частотой, что и физический маятник. Приравняв частоты 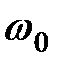 из уравнений (32.10) и (32.12), получаем: из уравнений (32.10) и (32.12), получаем:
 . .
Используя теорему Штейнера, определим приведенную длину  и период и период  для физического маятника: для физического маятника:
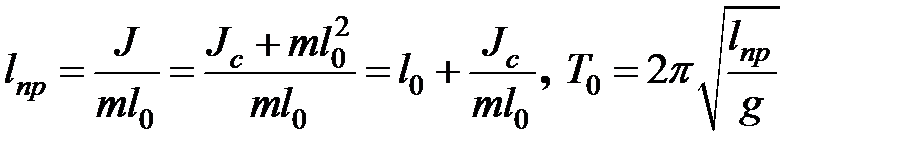 , (32.14) , (32.14)
где  – момент инерции физического маятника относительно оси, проходящей через центр – момент инерции физического маятника относительно оси, проходящей через центр  маятника и параллельной оси его качания. маятника и параллельной оси его качания.
Точка  , лежащая на прямой , лежащая на прямой  на расстоянии на расстоянии  от точки подвеса маятника от точки подвеса маятника  (рис. 32.3), называется центром качания физического маятника. Центр качания (рис. 32.3), называется центром качания физического маятника. Центр качания  и точка подвеса и точка подвеса  обладают свойством взаимности: если маятник подвесить так, чтобы его ось качания проходила через точку обладают свойством взаимности: если маятник подвесить так, чтобы его ось качания проходила через точку  , то точка , то точка  будет совпадать с новым положением центра качания маятника, то есть приведенная длина и период колебаний маятника останутся прежними. Это свойство физического маятника демонстрируется с помощью, так называемого оборотного маятника, который служит, в частности, для определения ускорения свободного паления в данной точке поверхности Земли. Для этого нужно на опыте измерить период будет совпадать с новым положением центра качания маятника, то есть приведенная длина и период колебаний маятника останутся прежними. Это свойство физического маятника демонстрируется с помощью, так называемого оборотного маятника, который служит, в частности, для определения ускорения свободного паления в данной точке поверхности Земли. Для этого нужно на опыте измерить период  , приведенную длину , приведенную длину  и воспользоваться формулой (32.14) для периода колебаний и воспользоваться формулой (32.14) для периода колебаний  . Тогда ускорение . Тогда ускорение  можно рассчитать по формуле можно рассчитать по формуле
 . .
Кинетическая энергия материальной точки, совершающей прямолинейные гармонические колебания, равна:
 . .
или
 . .
Кинетическая энергия материальной точки периодически изменяется от 0 до  , совершая гармонические колебания с циклической частотой , совершая гармонические колебания с циклической частотой  и амплитудой и амплитудой  около среднего значения, равного около среднего значения, равного  . .
Потенциальная энергия материальной точки, гармонически колеблющейся под действием квазиупругой силы, равна:
 , ,
или 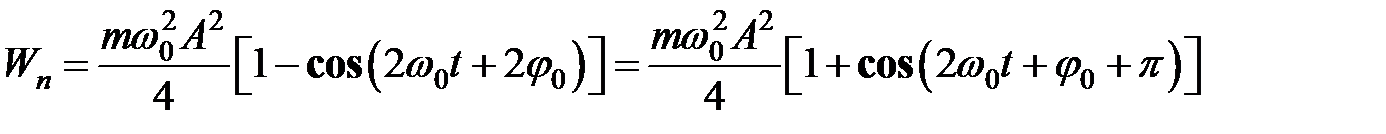 . .
Потенциальная энергия материальной точки периодически изменяется от 0 до  , совершая гармонические колебания с циклической частотой 2ω0 и амплитудой , совершая гармонические колебания с циклической частотой 2ω0 и амплитудой  около среднего значения, равного около среднего значения, равного  . .
Колебания потенциальной и кинетической энергии совершаются со сдвигом по фазе на  , так что полная механическая энергия материальной точки не изменяется при колебаниях: , так что полная механическая энергия материальной точки не изменяется при колебаниях:
 . .
Графики зависимости  , ,  , ,  от времени от времени  для случая для случая  показаны на рис. 32.4. показаны на рис. 32.4.
ГЛАВА 33
Вопросы:
Затухающие колебания. Дифференциальное уравнение
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


 , удовлетворяющий этому условию, называется периодом колебаний. За период колебаний
, удовлетворяющий этому условию, называется периодом колебаний. За период колебаний  , равная числу полных колебаний, совершающихся за единицу времени. Циклической, или круговой, частотой периодических колебаний называется величина
, равная числу полных колебаний, совершающихся за единицу времени. Циклической, или круговой, частотой периодических колебаний называется величина  , равная числу полных колебаний, совершающихся за
, равная числу полных колебаний, совершающихся за  единиц времени.
единиц времени. от времени
от времени  удовлетворяет условию
удовлетворяет условию  .
. называются гармоническими колебаниями, если физическая величина изменяется во времени по синусоидальному или косинусоидальному закону, то есть
называются гармоническими колебаниями, если физическая величина изменяется во времени по синусоидальному или косинусоидальному закону, то есть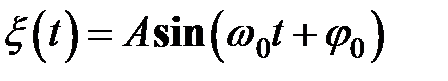 или
или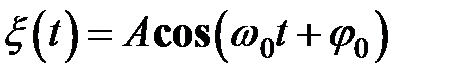 , (32.1)
, (32.1) – циклическая, или круговая, частота гармонических колебаний,
– циклическая, или круговая, частота гармонических колебаний,  – максимальное значение колеблющейся величины
– максимальное значение колеблющейся величины  , называемое амплитудой колебаний,
, называемое амплитудой колебаний,  и
и  постоянные величины. Значение
постоянные величины. Значение  (соответственно
(соответственно  ). Величины
). Величины  представляют собой начальные фазы колебаний, то есть значение
представляют собой начальные фазы колебаний, то есть значение  и
и  в момент (
в момент (  ) начала отсчета времени
) начала отсчета времени 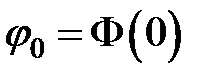 ,
,  .
. около положения равновесия, принятого за начало координат, то зависимость координаты
около положения равновесия, принятого за начало координат, то зависимость координаты  точки от времени
точки от времени  . (32.2)
. (32.2) и ускорения
и ускорения  точки на ось
точки на ось  ,
, , (32.3)
, (32.3) – амплитуда скорости,
– амплитуда скорости,  – амплитуда ускорения.
– амплитуда ускорения. , действующая на материальную точку, равна
, действующая на материальную точку, равна  и
и , (32.4)
, (32.4) – масса материальной точки. Следовательно, сила
– масса материальной точки. Следовательно, сила  пропорциональна смещению материальной точки из положения равновесия и стремится вернуть точку в положение равновесия.
пропорциональна смещению материальной точки из положения равновесия и стремится вернуть точку в положение равновесия. , (32.5)
, (32.5) – орт оси
– орт оси 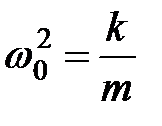 .
. . (32.6)
. (32.6) – вектор перемещения упруго деформированного тела при его продольном растяжении или сжатии,
– вектор перемещения упруго деформированного тела при его продольном растяжении или сжатии,  – коэффициент упругости.
– коэффициент упругости. или
или +
+  , (32.7)
, (32.7) (рис. 32.1). Такая система представляет собой линейный гармонический осциллятор. В произвольном положении
(рис. 32.1). Такая система представляет собой линейный гармонический осциллятор. В произвольном положении  на точку действует сила тяжести
на точку действует сила тяжести  , сила упругости
, сила упругости  , где
, где 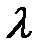 ст– статическая деформация в состоянии равновесия.
ст– статическая деформация в состоянии равновесия.



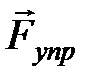




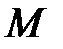

 ):
): . (32.8)
. (32.8)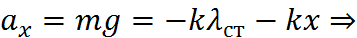
 , где
, где  , амплитуда
, амплитуда  и начальная фаза
и начальная фаза  и скорости
и скорости  в начальный момент времени
в начальный момент времени  .
.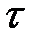 имеет вид:
имеет вид:

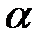






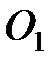
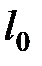



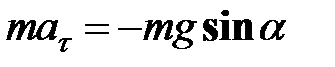 . (32.9)
. (32.9)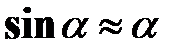 , получим дифференциальное уравнение осциллятора
, получим дифференциальное уравнение осциллятора 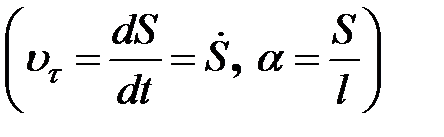 :
: ,
, . (32.10)
. (32.10) . В случае малых колебаний сила
. В случае малых колебаний сила 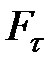 оказывается пропорциональной длине дуги
оказывается пропорциональной длине дуги 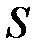
 , то есть совпадает по виду с упругой силой
, то есть совпадает по виду с упругой силой  в законе Гука и потому называется квазиупругой силой. Таким образом, причиной появления возвращающей силы в системе могут быть не только силы упругости, но и другие силы, например, сила тяжести при наличии связи в виде нити длиной
в законе Гука и потому называется квазиупругой силой. Таким образом, причиной появления возвращающей силы в системе могут быть не только силы упругости, но и другие силы, например, сила тяжести при наличии связи в виде нити длиной  в случае математического маятника.
в случае математического маятника. вокруг неподвижной горизонтальной оси
вокруг неподвижной горизонтальной оси  , не проходящей через центр тяжести тела (рис. 32.3) и называемой осью качания маятника (а также под действием реакции опоры оси
, не проходящей через центр тяжести тела (рис. 32.3) и называемой осью качания маятника (а также под действием реакции опоры оси  . Точка
. Точка 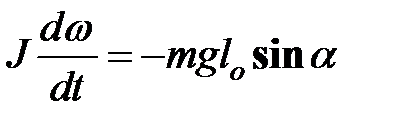 ,
, – момент инерции маятника относительно оси вращения.
– момент инерции маятника относительно оси вращения. получим уравнение осциллятора для вращательного движения
получим уравнение осциллятора для вращательного движения  :
: (32.11)
(32.11)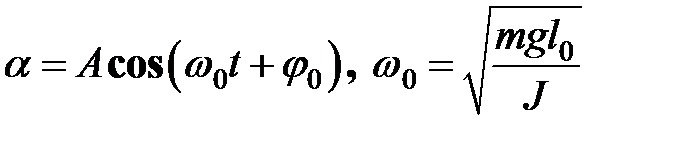 . (32.12)
. (32.12)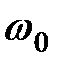 , периодом
, периодом (32.13)
(32.13) (
(  – максимальный угол поворота маятника вокруг оси вращения от положения равновесия).
– максимальный угол поворота маятника вокруг оси вращения от положения равновесия). такого математического маятника, который совершает колебания с той же частотой, что и физический маятник. Приравняв частоты
такого математического маятника, который совершает колебания с той же частотой, что и физический маятник. Приравняв частоты  .
. для физического маятника:
для физического маятника: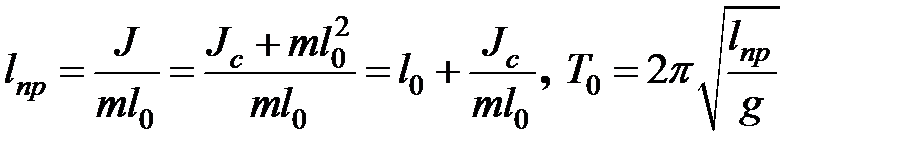 , (32.14)
, (32.14) – момент инерции физического маятника относительно оси, проходящей через центр
– момент инерции физического маятника относительно оси, проходящей через центр  маятника и параллельной оси его качания.
маятника и параллельной оси его качания. , лежащая на прямой
, лежащая на прямой  на расстоянии
на расстоянии  можно рассчитать по формуле
можно рассчитать по формуле .
. .
. .
. , совершая гармонические колебания с циклической частотой
, совершая гармонические колебания с циклической частотой  и амплитудой
и амплитудой  около среднего значения, равного
около среднего значения, равного  ,
,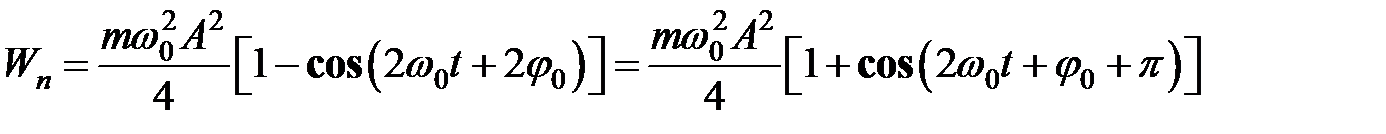 .
. , совершая гармонические колебания с циклической частотой 2ω0 и амплитудой
, совершая гармонические колебания с циклической частотой 2ω0 и амплитудой  около среднего значения, равного
около среднего значения, равного  , так что полная механическая энергия материальной точки не изменяется при колебаниях:
, так что полная механическая энергия материальной точки не изменяется при колебаниях: .
. ,
,  ,
,  от времени
от времени  показаны на рис. 32.4.
показаны на рис. 32.4.