
|
|
Затухающих колебаний и его решениеЛогарифмический декремент затухания Добротность колебательной системы
Затухающими механическими колебаниями называются колебания, амплитуда которых непрерывно уменьшается вследствие потерь механической энергии. В отсутствие сил трения движение под действием квазиупругой силы описывается дифференциальным уравнением (1.7). Однако, во всякой реальной колебательной системе имеются силы сопротивления (диссипативные силы), действие которых приводит к уменьшению энергии системы. Диссипация (от лат. dissipatio – рассеяние) энергии вызывается главным образом трением и возбуждением в окружающей среде упругих волн. Если убыль энергии не восполняется за счет работы внешних сил, колебания будут затухать. В случае малых отклонений от положения равновесия и малых скоростей движение осциллятора определяется квазиупругой силой
Применив обозначения
(см. (32.7)), перепишем уравнение (33.1) в виде:
Это линейное однородное дифференциальное уравнение второго порядка описывает затухающие колебания системы. Здесь
В случае малого сопротивления, когда
где
В том, что выражение (33.4) является решением дифференциального уравнения (33.3), можно убедиться путем подстановки его в это уравнение. На рис. 33.4 зависимость
Затухающие колебания представляют собой, вообще говоря, непериодические колебания, так как в этом случае не повторяются максимальные значения смещения, скорости и ускорения осциллятора. Однако если затухание мало, можно условно пользоваться понятием периода как промежутка времени между, например, двумя последовательными максимумами (минимумами) колеблющейся физической величины. Тогда период затухающих колебаний определяется выражением
т.е. Величины Логарифмическим декрементом затухания называется безразмерная величина
Промежуток времени
Определим число
С учетом соотношения (33.6) выражение для амплитуды
где Добротностью колебательной системы называется безразмерная физическая величина
Поскольку энергия
При малых значениях логарифмического декремента затухания
При этом условный период затухающих колебаний
Согласно формуле (33.12), добротность
ГЛАВА 34 Вопросы: Вынужденные колебания. Дифференциальное уравнение 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
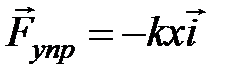 (1.5) и силой сопротивления Стокса
(1.5) и силой сопротивления Стокса  (здесь
(здесь 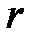 – постоянная, называемая коэффициентом сопротивлении, знак «–» обусловлен тем, что сила
– постоянная, называемая коэффициентом сопротивлении, знак «–» обусловлен тем, что сила  и скорость
и скорость 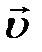 имеют противоположные направления). В связи с этим дифференциальное уравнение движения (уравнение второго закона Ньютона) в проекции на ось
имеют противоположные направления). В связи с этим дифференциальное уравнение движения (уравнение второго закона Ньютона) в проекции на ось  будет иметь вид
будет иметь вид или
или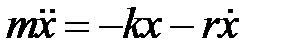 . (33.1)
. (33.1)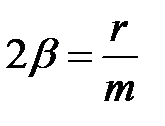 ,
, 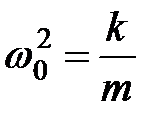 , (33.2)
, (33.2)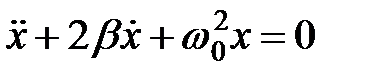 (33.3)
(33.3)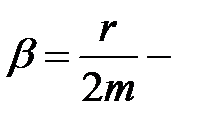 коэффициент затухания,
коэффициент затухания,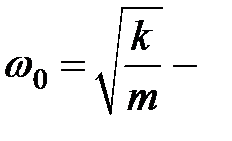 собственная циклическая частота осциллятора.
собственная циклическая частота осциллятора. , решение дифференциального уравнения (33.3) будет содержать показательную функцию (
, решение дифференциального уравнения (33.3) будет содержать показательную функцию (  ) и гармоническую функцию частоты
) и гармоническую функцию частоты 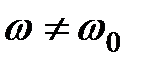 :
: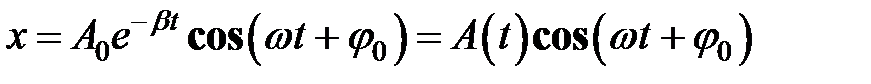 , (33.4)
, (33.4)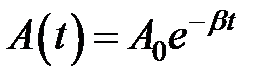 – амплитуда затухающих колебаний, соответственно
– амплитуда затухающих колебаний, соответственно  начальная амплитуда;
начальная амплитуда;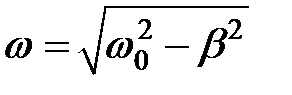 – циклическая частота этих колебаний;
– циклическая частота этих колебаний; – постоянные, которые зависят от начальных условий, т.е. от значений
– постоянные, которые зависят от начальных условий, т.е. от значений  и
и 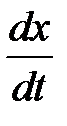 в начальный момент времени (
в начальный момент времени (  ).
).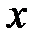

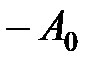
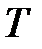
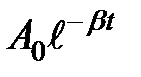

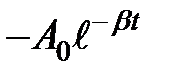

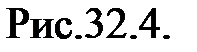
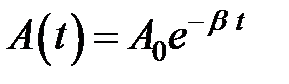 представлена штриховой линией,
представлена штриховой линией,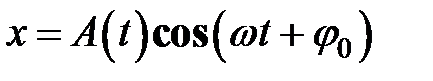 – сплошной линией.
– сплошной линией.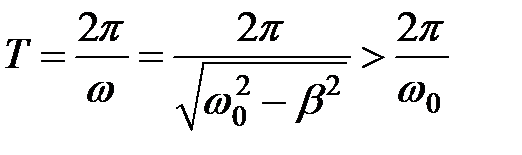 , (33.5)
, (33.5) .
.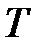 и
и 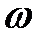 называют условным периодом и условной циклической частотой затухающих колебаний.
называют условным периодом и условной циклической частотой затухающих колебаний.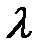 , равная натуральному логарифму отношения значений амплитуд
, равная натуральному логарифму отношения значений амплитуд 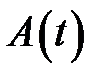 и
и 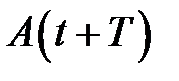 двух последовательных колебаний, отличающихся на период
двух последовательных колебаний, отличающихся на период 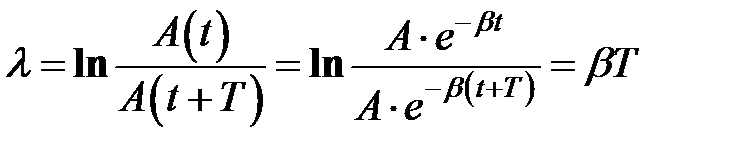 (33.6)
(33.6)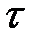 , в течение которого амплитуда колебаний уменьшается в
, в течение которого амплитуда колебаний уменьшается в 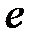 раз, называется временем релаксации. Тогда
раз, называется временем релаксации. Тогда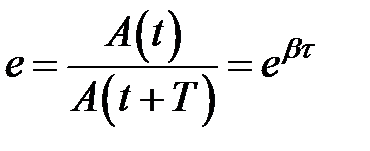 ,
, 
 . (33.7)
. (33.7)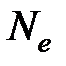 полных колебаний за время релаксации
полных колебаний за время релаксации 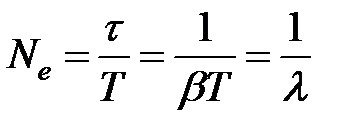 . (33.8)
. (33.8) , (33.9)
, (33.9) число полных колебаний за время
число полных колебаний за время  .
.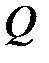 , равная произведению
, равная произведению  на отношение энергии
на отношение энергии  колебаний системы в произвольный момент времени
колебаний системы в произвольный момент времени  , т.е. за один условный период затухающих колебаний:
, т.е. за один условный период затухающих колебаний: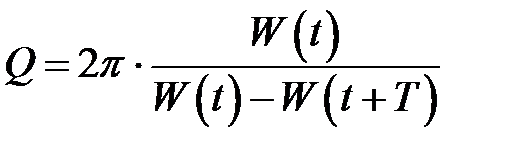 . (33.10)
. (33.10)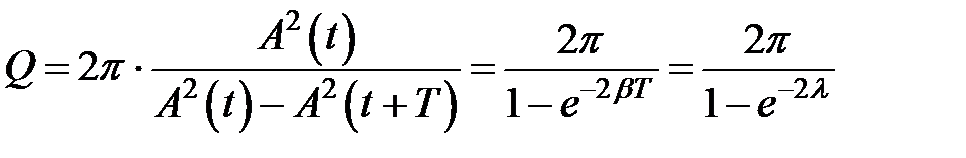 . (33.11)
. (33.11)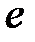 в ряд Тейлора
в ряд Тейлора 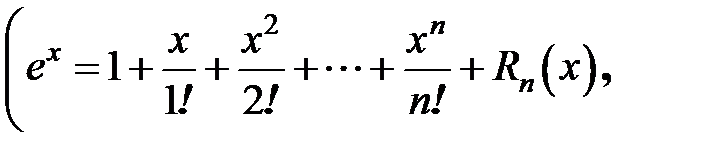
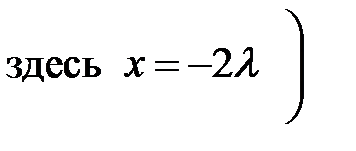 и ограничиваясь первыми двумя слагаемыми разложения, получаем:
и ограничиваясь первыми двумя слагаемыми разложения, получаем: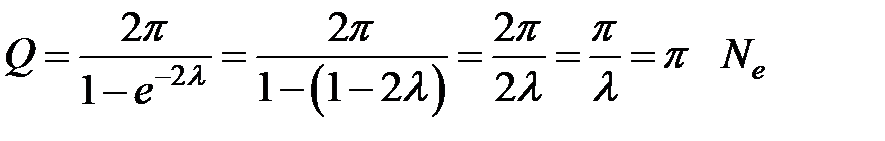 . (33.12)
. (33.12)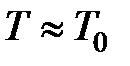 , так что
, так что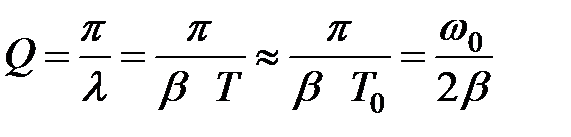 . (33.13)
. (33.13)