Вынужденных колебаний и его решение
Амплитуда и фаза вынужденных колебаний
Явление резонанса. Резонансные кривые
Поскольку свободные механические колебания реальной системы являются затухающими, то для поддержания таких колебаний используют переменную внешнюю силу, приложенную к системе. Ее называют вынуждающей, или возмущающей силой, а сами колебания называются вынужденными колебаниями, совершающимися с частотой возмущающей силы. Пусть на материальную точку вдоль оси  действуют возвращающая сила действуют возвращающая сила  и вынуждающая внешняя сила, которая изменяется во времени по гармоническому закону и вынуждающая внешняя сила, которая изменяется во времени по гармоническому закону  . Тогда дифференциальное уравнение движения материальной точки имеет вид: . Тогда дифференциальное уравнение движения материальной точки имеет вид:
 , , 
 , (34.1) , (34.1)
где  ; ;  ; ;  . .
Общее решение этого уравнения состоит из двух решений:
 . (34.2) . (34.2)
Здесь  общее решение однородного дифференциального уравнения вида (33.3); общее решение однородного дифференциального уравнения вида (33.3);
 частное решение неоднородного дифференциального уравнения (34.1). частное решение неоднородного дифференциального уравнения (34.1).
Первое слагаемое, т.е.  быстро затухает быстро затухает  . Поэтому при . Поэтому при  вклад в решение (34.2) дает только частное решение (второе слагаемое), которое представляет собой вынужденные гармонические колебания осциллятора с частотой, равной частоте вынуждающей силы, т.е. вклад в решение (34.2) дает только частное решение (второе слагаемое), которое представляет собой вынужденные гармонические колебания осциллятора с частотой, равной частоте вынуждающей силы, т.е.
 . (34.3) . (34.3)
Такой осциллятор является системой, в которой можно возбудить механические колебания.
Выражения для амплитуды  и сдвиг фазы и сдвиг фазы 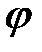 найдем, подставив в дифференциальное уравнение (34.1) решение (34.3) и его производные: найдем, подставив в дифференциальное уравнение (34.1) решение (34.3) и его производные:
 , ,
 , ,
 . .
В результате подстановки получим тригонометрическое уравнение:
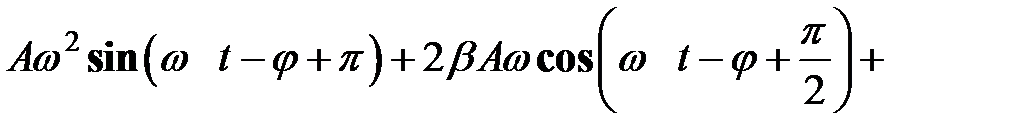
 (34.4) (34.4)
Уравнение (34.4) показывает, что сумма трех одинаково направленных гармонических колебаний с амплитудами
 , ,  , ,  и различными начальными фазами и различными начальными фазами  , , 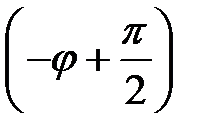 и и  должна совпадать с гармоническим колебанием, происходящим по закону должна совпадать с гармоническим колебанием, происходящим по закону  с амплитудой с амплитудой 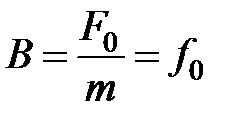 . .
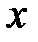 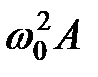 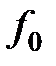      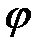  Уравнение (34.4) решим с помощью векторной диаграммы (рис. 34.1), осуществив сложение трех гармонических функций в левой части этого уравнения.
Из рисунка следует, что
 , (34.5) , (34.5)
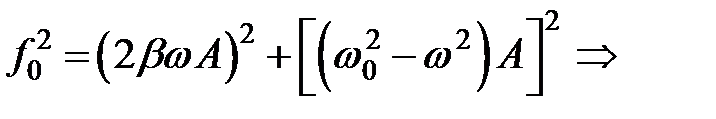
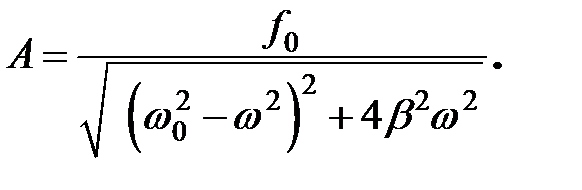 (34.6) (34.6)
Подставив в уравнение (34.3) значения  и и 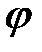 , определяемые формулами (34.5) и (34.6), получим функцию: , определяемые формулами (34.5) и (34.6), получим функцию:
 . (34.7) . (34.7)
Обратим внимание на тот факт, что амплитуда  и начальная фаза и начальная фаза 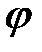 вынужденных колебаний определяются не начальными условиями, а значениями вынужденных колебаний определяются не начальными условиями, а значениями  и частоты и частоты 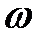 вынуждающей силы, а также параметрами осциллятора вынуждающей силы, а также параметрами осциллятора  . .
Исследуем выражения (34.5) и (34.6) как функции частоты 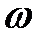 и построим их графики (рис. 34.2, рис. 34.3). и построим их графики (рис. 34.2, рис. 34.3).
              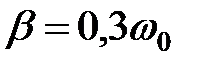  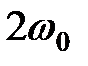  
Очевидно, что максимуму амплитуды  соответствует минимум знаменателя или его подкоренного выражения. Тогда, исследуя покоренное выражение знаменателя на экстремум, продифференцировав его по соответствует минимум знаменателя или его подкоренного выражения. Тогда, исследуя покоренное выражение знаменателя на экстремум, продифференцировав его по 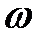 , получим уравнение: , получим уравнение:
 (34.8) (34.8)
Его решение имеет три корня:
 , ,  . (34.9) . (34.9)
Из двух корней  и и  физический смысл имеет лишь положительный корень, определяющий резонансную частоту внешней периодической силы: физический смысл имеет лишь положительный корень, определяющий резонансную частоту внешней периодической силы:
 , (34.10) , (34.10)
которой соответствует максимальное (резонансное) значение амплитуды:
 .(34.11) .(34.11)
При  , т.е. при малом затухании: , т.е. при малом затухании:
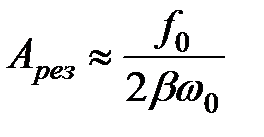 . (34.12) . (34.12)
На рис. 34.2 показаны зависимости амплитуды вынужденных колебаний от частоты вынуждающей силы; отдельные кривые на графике соответствуют различным значениям параметра  . В соответствии с (34.10) и (34.11), чем меньше . В соответствии с (34.10) и (34.11), чем меньше  , тем выше и правее лежит максимум данной кривой, и тем «острее» он получается. При очень большом затухании (таком, что , тем выше и правее лежит максимум данной кривой, и тем «острее» он получается. При очень большом затухании (таком, что  ) выражение (3.10) для резонансной частоты становится мнимым. Это означает, что резонанс при таких условиях не наблюдается – с увеличением частоты амплитуда вынужденных колебаний монотонно убывает (см. нижнюю кривую на рис. 34.2). Изображенные на рис. 34.2 графики функции (34.6), соответствующие различным значениям параметра ) выражение (3.10) для резонансной частоты становится мнимым. Это означает, что резонанс при таких условиях не наблюдается – с увеличением частоты амплитуда вынужденных колебаний монотонно убывает (см. нижнюю кривую на рис. 34.2). Изображенные на рис. 34.2 графики функции (34.6), соответствующие различным значениям параметра  , называются резонансными кривыми. , называются резонансными кривыми.
По поводу резонансных кривых необходимо отметить следующее. При стремлении 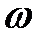 к нулю амплитуда вынужденных колебаний стремится к одному и тому же, отличному от нуля, предельному значению, равному к нулю амплитуда вынужденных колебаний стремится к одному и тому же, отличному от нуля, предельному значению, равному  . Это значение представляет собой смещение . Это значение представляет собой смещение  из положения равновесия, которое получает колебательная система под действием постоянной силы из положения равновесия, которое получает колебательная система под действием постоянной силы  , т.е. , т.е.
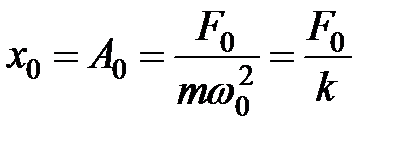 . (34.13) . (34.13)
При стремлении 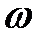 к бесконечности все кривые асимптотически стремятся к нулю. Это объясняется тем, что при большой частоте вынуждающая сила настолько изменяет свое направление, что осциллятор (колебательная система) не успевает заметно сместиться из положения равновесия. к бесконечности все кривые асимптотически стремятся к нулю. Это объясняется тем, что при большой частоте вынуждающая сила настолько изменяет свое направление, что осциллятор (колебательная система) не успевает заметно сместиться из положения равновесия.
Установим связь добротности осциллятора при малом затухании (т.е. при  ) с резонансной амплитудой. Разделим выражение (34.12) на смещение ) с резонансной амплитудой. Разделим выражение (34.12) на смещение  от положения равновесия под действием постоянной силы от положения равновесия под действием постоянной силы  (34.13): (34.13):
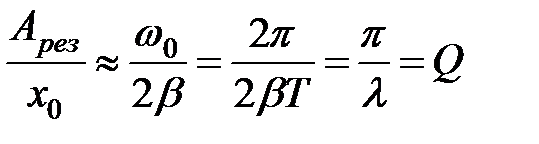 , (34.14) , (34.14)
(см. формулу (33.13)). Таким образом, добротность 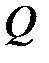 показывает, во сколько раз амплитуда в момент резонанса превышает смещение системы из положения равновесия под действием постоянной силы той же величины, что и амплитуда вынуждающей силы (это справедливо лишь при небольшом затухании). показывает, во сколько раз амплитуда в момент резонанса превышает смещение системы из положения равновесия под действием постоянной силы той же величины, что и амплитуда вынуждающей силы (это справедливо лишь при небольшом затухании).
Зависимость сдвига фазы 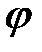 вынужденных колебаний от частоты вынужденных колебаний от частоты  возмущающей силы возмущающей силы 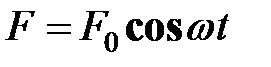 показана на рис. 34.3. Из рис. 34.1 видно, что вынужденные колебания отстают по фазе от вынуждающей силы, причем величина отставания показана на рис. 34.3. Из рис. 34.1 видно, что вынужденные колебания отстают по фазе от вынуждающей силы, причем величина отставания 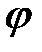 лежит в пределах от нуля до лежит в пределах от нуля до  (рис. 34.3). Частота (рис. 34.3). Частота 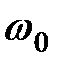 соответствует соответствует  . Резонансная частота меньше собственной (см. формулу (34.10)). Следовательно, в момент резонанса . Резонансная частота меньше собственной (см. формулу (34.10)). Следовательно, в момент резонанса  . При слабом затухании . При слабом затухании  , и значение , и значение 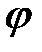 при резонансе можно считать равным при резонансе можно считать равным  . Из рис. 34.3 также видно, что при малых частотах вынуждающей силы ( . Из рис. 34.3 также видно, что при малых частотах вынуждающей силы (  ) числовое значение ) числовое значение 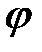 меньше меньше  , а при частотах, больших, чем собственная частота осциллятора, , а при частотах, больших, чем собственная частота осциллятора, 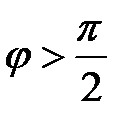  . .
Явление механического резонанса может быть как вредным, так и полезным. В связи с этим при конструировании машин, зданий, сооружений нужно подбирать их параметры так, чтобы собственная частота колебаний не совпадала с частотой возможных внешних воздействий. В противном случае резонансные колебания могут вызвать серьезные разрушения. С другой стороны, явление резонанса позволяет исследовать даже слабые колебания, например, в акустике для анализа звуков и их усиления.
На величину амплитуды колебаний (см. формулу (34.6)) можно воздействовать посредством внешней силы, но и косвенно, путем изменения тех параметров системы, которые определяют частоту собственных колебаний. Сюда относятся длина  маятника, коэффициенты маятника, коэффициенты  возвращающих сил и др. Такие колебания называются параметрическими. Если в процессе изменения параметров системы под действием внешней силы над системой будет совершена положительная работа, тогда энергия системы возрастает, что приведет к увеличению амплитуды колебаний. Это явление называется параметрическим резонансом возвращающих сил и др. Такие колебания называются параметрическими. Если в процессе изменения параметров системы под действием внешней силы над системой будет совершена положительная работа, тогда энергия системы возрастает, что приведет к увеличению амплитуды колебаний. Это явление называется параметрическим резонансом
ГЛАВА 35 Вопросы:
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


 действуют возвращающая сила
действуют возвращающая сила  и вынуждающая внешняя сила, которая изменяется во времени по гармоническому закону
и вынуждающая внешняя сила, которая изменяется во времени по гармоническому закону  . Тогда дифференциальное уравнение движения материальной точки имеет вид:
. Тогда дифференциальное уравнение движения материальной точки имеет вид: ,
, 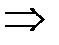
 , (34.1)
, (34.1) ;
;  ;
;  .
. . (34.2)
. (34.2) общее решение однородного дифференциального уравнения вида (33.3);
общее решение однородного дифференциального уравнения вида (33.3); частное решение неоднородного дифференциального уравнения (34.1).
частное решение неоднородного дифференциального уравнения (34.1). быстро затухает
быстро затухает  . Поэтому при
. Поэтому при  вклад в решение (34.2) дает только частное решение (второе слагаемое), которое представляет собой вынужденные гармонические колебания осциллятора с частотой, равной частоте вынуждающей силы, т.е.
вклад в решение (34.2) дает только частное решение (второе слагаемое), которое представляет собой вынужденные гармонические колебания осциллятора с частотой, равной частоте вынуждающей силы, т.е. . (34.3)
. (34.3) и сдвиг фазы
и сдвиг фазы 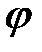 найдем, подставив в дифференциальное уравнение (34.1) решение (34.3) и его производные:
найдем, подставив в дифференциальное уравнение (34.1) решение (34.3) и его производные: ,
, .
.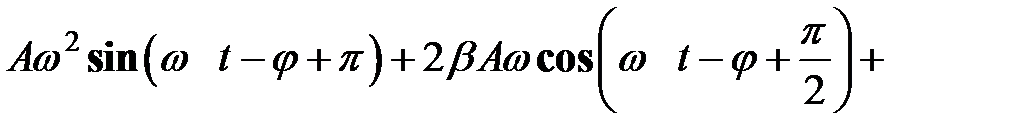
 (34.4)
(34.4) ,
,  ,
,  и различными начальными фазами
и различными начальными фазами  ,
, 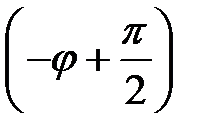 и
и  должна совпадать с гармоническим колебанием, происходящим по закону
должна совпадать с гармоническим колебанием, происходящим по закону  с амплитудой
с амплитудой 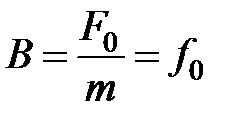 .
.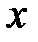
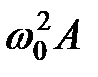
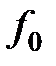





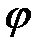

 , (34.5)
, (34.5)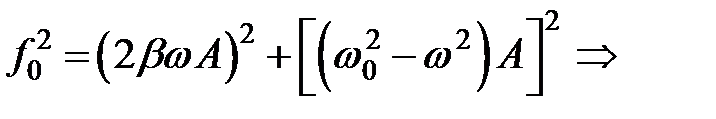
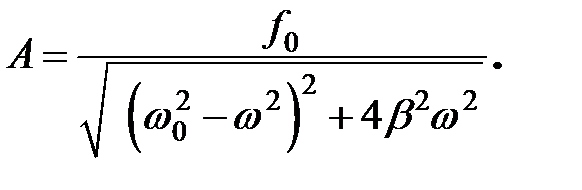 (34.6)
(34.6) . (34.7)
. (34.7)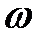 вынуждающей силы, а также параметрами осциллятора
вынуждающей силы, а также параметрами осциллятора  .
.










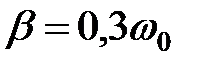

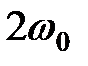


 (34.8)
(34.8) ,
,  . (34.9)
. (34.9) и
и  физический смысл имеет лишь положительный корень, определяющий резонансную частоту внешней периодической силы:
физический смысл имеет лишь положительный корень, определяющий резонансную частоту внешней периодической силы: , (34.10)
, (34.10) .(34.11)
.(34.11) , т.е. при малом затухании:
, т.е. при малом затухании: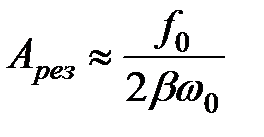 . (34.12)
. (34.12) . В соответствии с (34.10) и (34.11), чем меньше
. В соответствии с (34.10) и (34.11), чем меньше  ) выражение (3.10) для резонансной частоты становится мнимым. Это означает, что резонанс при таких условиях не наблюдается – с увеличением частоты амплитуда вынужденных колебаний монотонно убывает (см. нижнюю кривую на рис. 34.2). Изображенные на рис. 34.2 графики функции (34.6), соответствующие различным значениям параметра
) выражение (3.10) для резонансной частоты становится мнимым. Это означает, что резонанс при таких условиях не наблюдается – с увеличением частоты амплитуда вынужденных колебаний монотонно убывает (см. нижнюю кривую на рис. 34.2). Изображенные на рис. 34.2 графики функции (34.6), соответствующие различным значениям параметра  . Это значение представляет собой смещение
. Это значение представляет собой смещение  из положения равновесия, которое получает колебательная система под действием постоянной силы
из положения равновесия, которое получает колебательная система под действием постоянной силы  , т.е.
, т.е.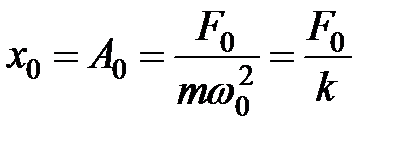 . (34.13)
. (34.13)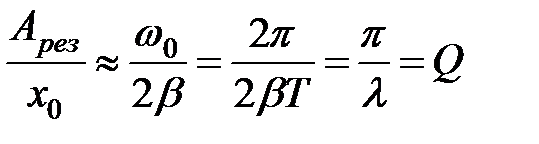 , (34.14)
, (34.14)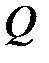 показывает, во сколько раз амплитуда в момент резонанса превышает смещение системы из положения равновесия под действием постоянной силы той же величины, что и амплитуда вынуждающей силы (это справедливо лишь при небольшом затухании).
показывает, во сколько раз амплитуда в момент резонанса превышает смещение системы из положения равновесия под действием постоянной силы той же величины, что и амплитуда вынуждающей силы (это справедливо лишь при небольшом затухании). возмущающей силы
возмущающей силы 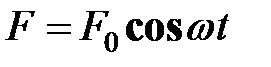 показана на рис. 34.3. Из рис. 34.1 видно, что вынужденные колебания отстают по фазе от вынуждающей силы, причем величина отставания
показана на рис. 34.3. Из рис. 34.1 видно, что вынужденные колебания отстают по фазе от вынуждающей силы, причем величина отставания  (рис. 34.3). Частота
(рис. 34.3). Частота 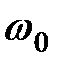 соответствует
соответствует  . Резонансная частота меньше собственной (см. формулу (34.10)). Следовательно, в момент резонанса
. Резонансная частота меньше собственной (см. формулу (34.10)). Следовательно, в момент резонанса  . При слабом затухании
. При слабом затухании  , и значение
, и значение  . Из рис. 34.3 также видно, что при малых частотах вынуждающей силы (
. Из рис. 34.3 также видно, что при малых частотах вынуждающей силы (  ) числовое значение
) числовое значение 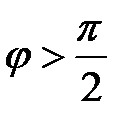
 .
. маятника, коэффициенты
маятника, коэффициенты  возвращающих сил и др. Такие колебания называются параметрическими. Если в процессе изменения параметров системы под действием внешней силы над системой будет совершена положительная работа, тогда энергия системы возрастает, что приведет к увеличению амплитуды колебаний. Это явление называется параметрическим резонансом
возвращающих сил и др. Такие колебания называются параметрическими. Если в процессе изменения параметров системы под действием внешней силы над системой будет совершена положительная работа, тогда энергия системы возрастает, что приведет к увеличению амплитуды колебаний. Это явление называется параметрическим резонансом