
|
|
Элементы квантовой статистикиРаспределение свободных электронов в металле по энергиям при 0 K - справедливое при e < eF (где eF - энергия или уровень Ферми)
где dn(e) - концентрация электронов, энергия которых заключена в пределах от e до e + de; m - масса электрона. Энергия Ферми в металле при T = 0 K
где n - концентрация электронов в металле.
2.6. Полупроводники Удельная проводимость собственных полупроводников g = go×exp(-DE/2kT), где DE - ширина запрещённой зоны; g0 - константа. Сила тока в p-n переходе I = Io[exp(eU/kT) - 1], где Io - предельное значение силы обратного тока; U - внешнее напряжение, приложенное к p-n переходу.
2.7. Контактные и термоэлектрические явления Внутренняя контактная разность потенциалов U12 = (eF1 - eF2)/e, где eF1 и eF2 - энергия Ферми соответственно для первого и второго металлов; e - заряд электрона.
Примеры решения задач Пример 1. Электрон в атоме водорода перешел с четвёртого энергетического уровня на второй. Определить энергию испущенного при этом фотона. Решение. Для определения энергии фотона воспользуемся сериальной формулой Бальмера для водородоподобных ионов:
где l - длина волны фотона; R - постоянная Ридберга; Z - заряд ядра в относительных единицах (при Z = 1 формула переходит в сериальную формулу для водорода); n1 - номер орбиты, с которой перешел электрон; n2 - номер орбиты, на которую перешел электрон ( n1 и n2 - главные квантовые числа). Энергия фотона e выражается формулой e = h×c/l Поэтому, умножив обе части равенства (1) на hc, получим выражение для энергии фотона:
Так как Rhc есть энергия ионизации Ei атома водорода, то
Вычисления выполним во внесистемных единицах: Ei = 13,6 эВ. Z = 1; n1 = 2; n2 = 4: e = 13,6×12(1/22 - 1/42) эВ = 13,6×3/16 = 2,55 эВ.
Пример 2. Электрон, начальной скоростью которого можно пренебречь, прошел ускоряющую разность потенциалов U. Найти длину волны де Бройля электрона для двух случаев: 1) U1 = 51 В; 2) U2 = 510 кВ. Решение. Длина волны де Бройля для частицы зависит от её импульса p и определяется формулой lБ = h/p, (1) где h - постоянная Планка. Импульс частицы можно определить, если известна её кинетическая энергия T. Связь импульса с кинетической энергией различна для нерелятивистского случая (когда кинетическая энергия частицы много меньше её энергии покоя) и для релятивистского случая (когда кинетическая энергия сравнима с энергией покоя частицы). В нерелятивистском случае
где mo - масса покоя электрона. В релятивистском случае
где Eo = moc2 - энергия покоя электрона.
Формула (1) с учётом соотношений (2) и (3) запишется: в нерелятивистском случае
в релятивистском случае
Сравним кинетические энергии электрона, прошедшего заданные в условии задачи разности потенциалов U1 = 51 В и U2 = 510 кВ, с энергией покоя электрона и в зависимости от этого решим, какую из формул (4) или (5) следует применить для вычисления длины волны де Бройля. Электрическое поле совершает над электроном работу, которая равна изменению его кинетической энергии T: T = e×U В первом случае T1 = e×U = 51 эВ = 0,51×10-4 МэВ, что много меньше энергии покоя электрона Eo = moc2 = 0,51 МэВ. Следовательно, в этом случае можно применить формулу (4). Для упрощения расчётов заметим, что T1 = =10-4moc2. Подставив это выражение в формулу (4), перепишем её в виде
Учитывая, что h/moc есть комптоновская длина волны L, получим l1 = 102L× Так как L = 2,43 пм, то l1 = 102×2,43/ Во втором случае кинетическая энергия T2 = eU2 = 510 кэВ = 0,51МэВ, т.е. равна энергии покоя электрона. В этом случае необходимо применить релятивистскую формулу (5). Так как T2 = moc2, то по формуле (5) находим
Подставим значение L и произведём вычисления:
Пример 3. Кинетическая энергия электрона в атоме водорода составляет величину порядка T = 10 эВ. Используя соотношение неопределённостей, оценить минимальные линейные размеры атома. Решение. Соотношение неопределённостей для координаты и импульса имеет вид Dx×Dpx ³ ћ, (1) где Dx - неопределённость координаты x электрона; Dpx - неопределённость проекции импульса электрона на ось X; ħ - постоянная Планка, делённая на 2p. Из соотношения неопределённостей следует, что чем точнее определяется положение частицы в пространстве, тем более неопределённым становится соответствующая проекция импульса, а следовательно, и энергия частицы. Пусть атом имеет линейные размеры l, тогда электрон атома будет находиться где-то в пределах области с неопределённостью Dx = l/2. Соотношение неопределённостей (1) можно записать в том случае в виде (l/2)Dpx ³ ħ, откуда l ³ 2ħ/Dpx. (2) Физически разумная неопределённость импульса Dpx во всяком случае не должна превышать значения самого импульса px, то есть Dpx £ px. Импульс px связан с кинетической энергией T соотношением px = (2mT)1/2. Переходя от неравенства к равенству, получим
Произведём вычисления: lmin = 2×1,05×10-34/(2×9,1×10-31×1,6×10-19×10)1/2 = 124 нм.
Пример 4. Волновая функция 2) в средней части ящика ((l - Dl)/2 ≤ x ≤(l + Dl)/2). Решение. Вероятность того, что частица будет обнаружена в интервале dx (от x до x + dx), пропорциональна этому интервалу и квадрату модуля волновой функции, описывающей данное состояние, равна dw = êy(x)ê2×dx. В первом случае искомая вероятность найдётся интегрированием в пределах от 0 до 0,01l:
Так как x изменяется в интервале 0 ≤x ≤0,01l и, следовательно, px/l <l, справедливо приближённое равенство sin2(px/l) » (px/l)2. С учётом этого выражение (1) примет вид
После интегрирования получим w = Во втором случае можно обойтись без интегрирования, так как квадрат модуля волновой функции вблизи её максимума в заданном малом интервале (Dl = =0,01l) практически не изменяется. Искомая вероятность во втором случае определяется выражением w = 2×(sin2(pl/2l)×Dl/l = 2×0,01l/l = 0,02.
Пример 5. Найти заряд ядра атомов вещества, для которых Ka-линия в характеристическом рентгеновском спектре имеет длину волны l=193,5 пм. Решение. По закону Мозли
Ответ: Q=+26e. Пример 6. На медную фольгу, у которой n×d = 1,5×10-2 кг/м2, падает перпендикулярно узкий пучок a - частиц, энергия которых 5,29 МэВ. На угол q > 6° рассеивается больше 1% всех a-частиц. Определить число протонов Z в ядре меди. Решение. Рассеяние a-частиц на ядрах атомов описывается формулой Резерфорда:
По условию задачи a частицы рассеиваются в пределах углов 6°<q <180°, поэтому число рассеянных a-частиц можно определить интегрированием:
По условию задачи DN/N ³ 0,01. Выполнив в (1) некоторые преобразования, получим
Для определения Z необходимо найти nd - число ядер фольги на единицу ее поверхности. В условии задачи дается rd, поэтому nd находим по формуле:
где m = 0,064 кг/моль, NА - число Авогадро. Количество протонов в ядре меди найдём из уравнения (2):
Пример 7. Узкий пучок протонов с кинетической энергией Т = 100 кэВ падает перпендикулярно на золотую фольгу, для которой rd = 102 кг/м2. Протоны под углом q=60° регистрирует счетчик с круглым отверстием S=1 см2, которое расположено на расстоянии R = 10 см от участка фольги, рассеивающей протоны. Отверстие счетчика расположено перпендикулярно к направлению падающих на него протонов. Доля рассеянных протонов, падающих на отверстие счетчика, составляет DN/N = 4×10-4. Определить массовое число ядра атома золота. Решение. Для нахождения массового числа А примем, что Мат » А×mN.и воспользуемся формулой :
В условии задачи задана площадь S, на которую под углом q в пределах Dq падают частицы. Поскольку площадка и количество частиц DN имеют определенные значения, уравнение (1) необходимо записать в интегральной форме:
Учитывая малые изменения углов q и j интеграл в выражении (2) запишем в следующем виде:
где q - среднее значение угла q. Используя приближение (3), определим А:
Ответ: А = 194. Пример 8. Вычислить сечение ядра атома золота, которое соответствует рассеянию протонов с кинетической энергией Т = МэВ в пределах углов q от 60° до 180°.
Решение. Рассеяние частиц ядром в пределах углов от q до q + dq определяется площадью ds эффективного сечения ядра в виде кольца (рис.1.1): ds = 2pbdb . (1) Прицельное расстояние b найдем из формулы:
где q1 - заряд протона, q2 - заряд ядра золота. Дифференциал от b равен:
Подставив выражение (2) и (3) в (1), получим:
Сечение ядра, на котором рассеиваются частицы в пределах углов от q1 до q2:
Подставим выражение (4) в интеграл (5):
После интегрирования получим:
где q1=+e, q2=78e.
Пример 9. Атомное ядро, поглотив g - фотон (l = 0,47 пм), возбудилось, после чего распалось на отдельные нуклоны, которые разлетелись в разных направлениях. Суммарная кинетическая энергия нуклонов равна 0,4 МэВ. Определить энергию связи Есв ядра. Решение. На основании закона сохранения энергии имеем: Мя + hn = Zmp + (А - Z)mn + Т, где Т - кинетическая энергия нуклонов. Энергия связи: Eсв = Z×mp + (A-Z)mn – Mя = hn - T. Eсв=hn - T = hc/l - T. Произведём вычисления
Ответ: Есв = 2,2 МэВ.
Пример 10. Рассчитать с помощью формулы Вейцзеккера энергию связи Са40. Решение. Полуэмпирическая формула Вейцзеккера позволяет найти энергию связи ядра по его значениям А и Z: Eсв=14A - 13A2/3 - 0,584Z2/A1/3 - 19,3 Для ядра Ca40 d = -1. Eсв = 14×40 - 13×402/3 - 0,58×202/402/3 – 19,3(40-40)/20 - 33,5×(-1)/403/4 = 342 МэВ. Ответ: Е. = 342 МэВ.
Пример 11. а) Определить с помощью формулы Вейцзеккера заряд Z ядра, которое имеет наименьшую массу среди ядер с одинаковым нечетным значением массового числа А. б)Определить с помощью полученной формулы характер активности следующих b активных ядер: Ag103 и Sn127.
Решение. а) Воспользовавшись формулой Вейцзеккера, выразим массу ядра как функцию А и Z: Mя = Z×mp + (A-Z)mn – 14A + 13A2/3 0,584×Z2/A1/3 +19,3× При заданном А масса ядра является функцией Z, т.е. Мя = f(Z) (рис.1.2). Чтобы найти Zmin, найдём производную dM/dZ и приравняем её к нулю:
Функция М(Z) имеет один минимум. Решив уравнение dM(Z)/dZ = 0 относительно Z, получим ответ на вопрос задачи: dM/dZ=mp-mn + 2Z×0,584/A1/3 +19,3× mp-mn=1,007276-1,008665=1,3 МэВ, 78,5=Z(154,4/A+1,17A-1/3). Zmin=78,5A/154,4+1,17A2/3=A/1,98+0,015A2/3. б) Определим Zmin для А = 103, Но Z может быть только целым числом, поэтому принимаем Zmin = 45. Радиоактивность Аg103 будет направлена на уменьшение Z, поэтому распад ядра идет по схеме:
Находим Zmin для А = 127:
Распад ядра
Ответ: Zmin = А/(1,98 + 0,015 А2/3). Пример 12. Вычислить дефект массы и энергию связи ядра Решение. Масса ядра всегда меньше суммы масс свободных (находящихся на очень больших расстояниях друг от друга ) протонов и нейтронов, из которых состоит ядро. Дефект массы ядра Dm равен разности между суммой масс свободных нуклонов и массой ядра, т.е. Dm = Zmp + (A - Z)mn - mя, (1) где Z - порядковый номер (число протонов в ядре); mp, mn, mя - соответственно массы протона , нейтрона и ядра. В справочных таблицах всегда даются массы нейтральных атомов, а не ядер, поэтому формулу (1) целесообразно преобразовать так, чтобы в неё входила масса ma нейтрального атома. Можно считать, что масса нейтрального атома равна сумме масс ядра и электронов, составляющих электронную оболочку ядра: ma = mя + Zme, откуда mя = ma - me. (2) Выразив в равенстве (1) массу ядра по формуле (2), получаем Dm = Z(mp + me) + (A - Z)mn - ma. Замечая, что mp+me=mH, где mH- масса атома водорода, находим Dm = ZmH + (A - Z)mn - ma. (3) Подставив в выражение (3) числовые значения масс, взятые из справочной таблицы, получим Dm = [3×1,00783 + (7 - 3)×1,00867 - 7×0,1601] = 0,04216 (а.е.м.) В соответствии с законом пропорциональности массы и энергии E = Dm×c2, (4) где c - скорость света в вакууме. Коэффициент пропорциональности c2 можно выразить через массу и энергию: c2 = E/Dm = 9×1016 Дж/кг. Если вычислять энергию связи, используя внесистемные единицы, то c2 = 931,44 МэВ/а.е.м. С учётом этого формула (4) примет вид E = 93,44×Dm (МэВ). (5) Подставив значение дефекта массы ядра в формулу (5), получим E = 931,44×0,04216 МэВ = 39,2 МэВ. Пример 13. Вычислить толщину слоя половинного ослабления X1/2 параллельного пучка g - излучения для воды, если линейный коэффициент ослабления m = 0,047 см-1. Решение. Интенсивность g - излучения в зависимости от толщины слоя убывает по закону: I = Ioexp(-mx). (1) Пройдя поглощающий слой половинного ослабления пучок будет иметь интенсивность I = Io/2. Подставив значения I и x в формулу (1), получим Io/2 = Ioexp(-m×x1/2), или после сокращения: 1/2 = exp(-mX1/2). (2) Прологарифмировав последнее выражение, получим искомое значение толщины слоя половинного ослабления: X1/2 = ln(2)/m. (3) Произведём вычисления X1/2 = ln(2)/4,7 = 14,7 см. Пример 14. Кремниевый образец нагревают от температуры t1 = 0oC до температуры t2 = 10oC. Во сколько раз возрастает его удельная проводимость? Решение. Удельная проводимость g собственных полупроводников связана с температурой T соотношением g = g0×exp(-DE/(2kT)), где g0 - константа; DE - ширина запрещённой зоны. Следовательно,
Полагая для кремния DE = 1,1 эВ, произведём вычисления:
КОНТРОЛЬНАЯ РАБОТА 6 Таблица вариантов
201. На сколько изменилась кинетическая энергия электрона в атоме водорода, если при переходе в невозбуждённое состояние атом излучил фотон с длиной волны l = 486 нм? 202. D-линия натрия излучается в результате такого перехода электрона с одной орбиты атома на другую, при котором энергия атома уменьшается на DW = 3,37×10-19 Дж. Найти длину волны l D-линии. 203. Электрон, пройдя разность потенциалов U = 4,9 В, сталкивается с атомом ртути и переводит его в первое возбуждённое состояние. Какую длину волны l имеет фотон, соответствующий переходу атома ртути в основное состояние? 204. Вычислить энергию e фотона, испускаемого при переходе электрона в атоме водорода с третьего энергетического уровня на первый. 205. Определить наименьшую emin и наибольшую emax энергии фотона в ультрафиолетовой серии спектра водорода (серии Лаймана). 206. Определить потенциальную П, кинетическую Т и полную Е энергии электрона, находящегося на первой орбите атома водорода. 207. Определить длину волны l, соответствующую третьей спектральной линии в серии Бальмера. 208. Найти наибольшую lmax и наименьшую lmin длины волн в первой инфракрасной серии спектра водорода (серии Пашена). 209. Вычислить длину волны l , которую испускает ион гелия Не+ при переходе со второго энергетического уровня на первый. Сделать такой же подсчет для иона лития Li++. 210. Найти энергию ионизации Ei и потенциал ионизации Ui ионов Не+ и Li++. 211. Вычислить частоты n1 и n2 вращения электрона в атоме водорода на второй и третьей орбитах. Сравнить эти частоты с частотой n излучения при переходе электрона с третьей на вторую орбиту. 212. Атом водорода в основном состоянии поглотил квант света с длиной волны l =121,5 нм. Определить радиус r электронной орбиты возбужден-ного атома водорода. 213. Определить первый потенциал U1 возбуждения атома водорода. 214. Атомарный водород, возбужденный светом определенной длины волны, при переходе в основное состояние испускает только три спектральные линии. Определить длины волн этих линий и указать, каким сериям они принадлежат. 215. Фотон с энергией e =16,5 эВ выбил электрон из невозбужденного атома водорода. Какую скорость V будет иметь электрон вдали от ядра атома? 216. На дифракционную решётку нормально падает пучок света от разрядной трубки, наполненной атомарным водородом. Постоянная решётки d=5 мкм. Какому переходу электрона соответствует спектральная линия, наблюдаемая при помощи этой решётки в спектре пятого порядка под углом j=41o? 217. Какую наименьшую энергию Wmin должны иметь электроны, чтобы при возбуждении атомов водорода ударами этих электронов появились все линии всех серий спектра водорода? Какую наименьшую скорость vmin должны иметь эти электроны? 218. Определить изменение энергии DE электрона в атоме водорода при излучении атомом фотона с частотой n = 6,28×1014 Гц. 219. Во сколько раз изменится период Т вращения электрона в атоме водорода, если при переходе в невозбуждённое состояние атом излучил фотон с длиной волны l= 97,5 нм? 220. В однозарядном ионе лития электрон перешёл с четвёртого энергетического уровня на второй. Определить длину волны l излучения, испущенного ионом лития. 221. В каких пределах должна лежать энергия бомбардирующих электронов, чтобы при возбуждении атомов водорода ударами этих электронов спектр водорода имел только одну спектральную линию? 222. В каких пределах должны лежать длины волн l монохроматического света, чтобы при возбуждении атомов водорода квантами этого света радиус орбиты электрона увеличился в 9 раз. 223. Вычислить радиусы r2 и r3 второй и третьей орбит в атоме водорода. 224. Определить скорость V электрона на второй орбите атома водорода. 225. Определить частоту обращения электрона на второй орбите атома водорода. 226. Какую энергию необходимо дополнительно сообщить электрону, чтобы его дебройлевская длина волны уменьшилась от 100 до 50 пм? 227. Две одинаковые нерелятивистские частицы движутся перпендикулярно друг к другу с дебройлевскими длинами волн l1 и l2. Найти дебройлевскую длину волны каждой частицы в системе центра инерции. 228. Найти дебройлевскую длину волны релятивистских электронов, подлетающих к антикатоду рентгеновской трубки, если длина волны коротковолновой границы сплошного рентгеновского спектра lk равна 10,0 пм. 229. При каком значении кинетической энергии дебройлевская длина волны электрона равна его комптоновской длине волны? 230. Из катодной трубки на диафрагму с узкой прямоугольной щелью нормально к плоскости диафрагмы направлен поток моноэнергетических электронов. Определить анодное напряжение трубки, если известно, что на экране, отстоящем от щели на расстоянии L = 0,5 м, ширина центрального дифракционногомаксимума Dx = 10,0 мкм. Ширину b щели принять равной 0,10 мм. 231. Параллельный поток электронов, ускоренных разностью потенциалов U = 25 В, падает нормально на диафрагму с двумя узкими щелями, расстояние между которыми d = 50 мкм. Определить расстояние между соседними максимумами дифракционной картины на экране, расположенном на расстоянии L = 100 см от щелей. 232. Найти дебройлевскую длину волны молекул водорода, соответствующую их наиболее вероятной скорости при комнатной температуре. 233. Найти длину волны де Бройля для электрона, движущегося по первой боровской орбите атома водорода. 234. Заряженная частица, ускоренная разностью потенциалов U = 200 В, имеет длину волны де Бройля lБ = 2,02 пм. Найти массу частицы, если её заряд численно равен заряду электрона. 235. Альфа-частица движется по окружности радиусом r = 8,3 мм в однородном магнитном поле, напряжённость которого H = 18,9 кА/м. Найти для неё длину волны де Бройля. 236. На сколько по отношению к комнатной должна измениться температура идеального газа, чтобы дебройлевская длина волны его молекул уменьшилась на 20%? 237. Вычислить наиболее вероятную дебройлевскую длину волны молекул водорода, находящихся в термодинамическом равновесии при комнатной температуре. 238. Кинетическая энергия электрона равна удвоенному значению его энергии покоя (2moc2). Вычислить длину волны де Бройля для такого электрона. 239. На грань некоторого кристалла под углом a = 60o к её поверхности падает параллельный пучок электронов, движущихся с одинаковой скоростью. Определить скорость v электронов, если они испытывают интерференционное отражение первого порядка. Расстояние d между атомными плоскостями кристалла равно 0, 2 нм. 240. Узкий пучок электронов, прошедших ускоряющую разность потенциалов U = 30 кВ, падает нормально на тонкий листок золота, проходит через него и рассеивается. На фотопластинке, расположенной за листком на расстоянии L = 20 см от него, получена дифракционная картина, состоящая из круглого центрального пятна и ряда концентрических окружностей. Радиус первой окружности r = 3,4 мм. Определить длину волны де Бройля электронов. 241. Параллельный пучок электронов, движущихся с одинаковой скоростью v= 1 Мм/с, падает нормально на диафрагму с длинной щелью шириной l = 1 мкм. Проходя через щель, электроны рассеиваются и образуют дифракционную картину на экране, расположенном на расстоянии d = 50 см от щели и параллельном плоскости диафрагмы. Определить линейное расстояние x между первыми дифракционными минимумами. 242. С какой скоростью движется электрон, если длина волны де Бройля электрона равна его комптоновской длине волны. 243. Электрон движется по окружности радиусом r = 0,5 см в однородном магнитном поле с индукцией B = 8 мТл. Определить длину волны де Бройля электрона. 244. Какую ускоряющую разность потенциалов должен пройти электрон, чтобы длина волны де Бройля была равна 1 пм? 245. Протон обладает кинетической энергией T = 1 кэВ. Определить дополнительную энергию DT, которую необходимо ему сообщить, для того, чтобы длина волны де Бройля уменьшилась в три раза. 246. Узкий пучок моноэнергетических электронов с кинетической энергией T= = 10 мэВ проходит через поликристаллическую алюминиевую фольгу, образуя на экране систему дифракционных колец. Вычислить межплоскостное расстояние, соответствующее отражению третьего порядка от некоторой системы кристаллических плоскостей, если ему отвечает дифракционное кольцо диаметра D = 3,20 см. Расстояние между экраном и фольгой L = 10,0 см. 247. Узкий пучок моноэнергетических электронов падает нормально на поверхность монокристалла никеля. В направлении, составляющем угол q = 550 с нормалью к поверхности, наблюдается максимум отражения четвёртого порядка при энергии электронов T =180 эВ. Вычислить соответствующее значение межплоскостного расстояния. 248. Вычислить дебройлевские длины волн электрона и атома урана, имеющих одинаковую кинетическую энергию 100 эВ. 249. Вычислить дебройлевскую длину волны релятивистского электрона, движущегося с кинетической энергией T = 0,3 МэВ. 250. Нейтрон с кинетической энергией T =25 эВ налетает на покоящийся дейтрон ( ядро тяжёлого водорода). Найти дебройлевские длины волн обеих частиц в системе их центра инерции. 251. Определить неточность Dx в определении координаты электрона, движущегося в атоме водорода со скоростью v = 1.5×106 м/с, если допускаемая неточность Dv в определении скорости составляет 10% от её величины. Сравнить полученную неточность с диаметром d атома водорода , вычисленным по теории Бора для основного состояния , и указать, применимо ли понятие траектории в данном случае. 252. Электрон с кинетической энергией T =1 эВ находится в металлической пылинке диаметром d =1 мкм. Определить относительную неточность Dv, с которой может быть определена скорость электрона. 253. Во сколько раз дебройлевская длина волны l частицы меньше не-определённости Dx её координаты, которая соответствует относительной неопределённости импульса в 1% ? 254. Предполагая , что неопределённость координаты движущейся частицы равна дебройлевской длине волны, определить относительную неточность Dp/p импульса этой частицы. 255. Используя соотношение неопределённостей, оценить ширину l одно-мерного потенциального ящика, в котором минимальная энергия электрона Emin = 10 эВ. 256. Используя соотношение неопределённостей, оценить низший энергети-ческий уровень электрона в атоме водорода. Принять линейные размеры атома d = 0,1 нм. 257. Приняв, что минимальная энергия E нуклона в ядре равна 10 МэВ, оценить, из соотношения неопределённостей, линейные размеры ядра. 258. Показать, используя соотношение неопределённостей, что в ядре не могут находится электроны. Линейные размеры ядра принять равными 5 фм. 259. Рассмотрим следующий мысленный эксперимент. Пусть моноэнерге-тический пучок электронов (Т=10 эВ) падает на щель шириной a. Можно сказать, что если электрон прошёл через щель, то его координата известна с неточностью Dx=a. Оценить полученную при этом относительную не-точность в определении импульса Dp/p электрона в случае, если а=0.1 нм. 260. Пылинки массой m = 10-12 г взвешены в воздухе и находятся в тепловом равновесии. Можно ли установить, наблюдая за движением пылинок, отклонение от законов классической механики? Принять, что воздух находится при нормальных условиях, пылинки имеют сферическую форму. Плотность вещества, из которого состоят пылинки, равна 2×103 кг/м3. 261. Используя соотношение неопределённостей DE×Dt ³ ħ, оценить ширину Г энергетического уровня в атоме водорода , находящегося : 1) в основном состоянии ; 2) в возбуждённом состоянии, время t жизни атома в возбуждённом состоянии равно 10-8 с. 262. Оценить относительную ширину Dw/w спектральной линии, если известны время жизни атома в возбуждённом состоянии t ~10-8 c и длина волны излучаемого фотона (l = 0,6 мкм ). 263. Какова должна быть кинетическая энергия протона в моноэнергетическом пучке, используемом для исследования структуры с линейными размерами l ~ 10-13 см. 264. Для приближенной оценки минимальной энергии электрона в атоме водорода можно предположить, что неопределённость Dr радиуса r электронной орбиты и неопределённость Dp импульса p электрона на такой орбите соответственно связаны следующим образом: Dr ~ r и Dp ~ p. Используя эти связи, а также соотношение неопределённостей, определить минимальное значение энергии Tmin электрона в атоме водорода. 265. Среднее время жизни Dt атома в возбуждённом состоянии составляет около 10-8 с. При переходе атома в нормальное состояние испускается фотон, средняя длина волны, которого равна 400 нм. Оценить относительную ширину Dl/l излучаемой спектральной линии, если не происходит уширения линии за счёт других процессов. 266. Электрон с кинетической энергией T ~ 4 МэВ локализован в области размером l = 1 мкм. Оценить с помощью соотношения неопределённостей относительную неопределённость его скорости. 267. Электрон находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Ширина ямы равна l=0,1 нм. Оценить с помощью соотношения неопределённостей силу давления электрона на стенки этой ямы при минимально возможной энергии. 268. Используя соотношение неопределённостей, оценить наименьшие ошибки Dv в определении скорости электрона и протона, если координаты центра масс этих частиц могут быть установлены с неопределённостью 1 мкм. 269. Альфа-частица находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике. Используя соотношение неопределённостей, оценить ширину l ящика, если известно, что минимальная энергия a - частицы Emin = 8 МэВ. 270. Принимая, что электрон находится внутри атома диаметром 0,3 нм, определить неопределённость энергии этого электрона. 271. Электронный пучок выходит из электронной пушки под действием разности потенциалов U = 200 В. Определить, можно ли одновременно измерить траекторию электрона с точностью до 100 пм и его скорость с точностью до 10%. 272. Оценить с помощью соотношения неопределённостей минимальную кинетическую энергию электрона, движущегося внутри сферы радиусом R = 0,05 нм. 273. Электронный пучок ускоряется в электронно-лучевой трубке разностью потенциалов U = 1 кВ. Известно, что неопределённость скорости составляет 0,1% от её числового значения. Определить неопределённость координаты электрона. Являются ли электроны в данных условиях квантовыми или классическими частицами? 274. Частица массы m = 9,1×10-31 кг движется в одномерном потенциальном поле U = k×x2/2 (гармонический осциллятор). Оценить с помощью соотношения неопределённостей минимально возможную энергию частицы в таком поле, если k = 1,12 Н/м. 275. Оценить с помощью соотношения неопределённостей минимально возможную энергию электрона в атоме водорода и соответствующее эффективное расстояние его от ядра. 276. Частица находится в потенциальном ящике. Найти отношение разности соседних энергетических уровней DEn+1,n к энергии Еn частицы в двух случаях: 1) n=3; 2) n®µ 277. Электрон находится в потенциальном ящике шириной l=0,5 нм. Опре-делить наименьшую разность DЕ энергетических уровней электрона. Ответ выразить в электрон-вольтах. 278. Частица в потенциальном ящике находится в основном состоянии. Какова вероятность W нахождения частицы: 1) в средней трети ящика; 2) в крайней трети ящика? 279. В одномерном потенциальном ящике шириной l находится электрон. Вычислить вероятность w нахождения электрона на первом энергетическом уровне в интервале 1/4, равноудаленном от стенок ящика. 280. Вычислить отношение вероятности w1/w2 нахождения электрона на первом и втором энергетических уровнях в интервале 1/4, равноудаленном от стенок одномерной потенциальной ямы шириной l. 281. Электрон находится в одномерном потенциальном ящике шириной l. Определить среднее значение координаты <x> электрона внутри ящика. 282. Волновая функция, описывающая движение электрона в основном состоянии атома водорода, имеет вид 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ,
,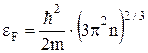 ,
, . (1)
. (1) .
.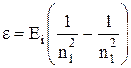 .
. ,
,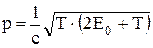 . (3)
. (3) , (4)
, (4) . (5)
. (5)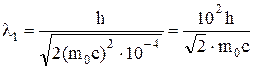 .
. .
. .
.
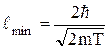 . (3)
. (3) описывает основное состояние частицы в бесконечно глубоком прямоугольном ящике шириной l. Вычислить вероятность нахождения частицы в малом интервале Dl = 0,01l в двух случаях: 1) вблизи стенки (0 < x < l);
описывает основное состояние частицы в бесконечно глубоком прямоугольном ящике шириной l. Вычислить вероятность нахождения частицы в малом интервале Dl = 0,01l в двух случаях: 1) вблизи стенки (0 < x < l); .
.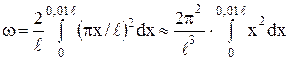 .
. .
.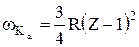 , где Z - зарядовое число ядра атома, R = 2,067×1016 с-1 Отсюда выразим Z
, где Z - зарядовое число ядра атома, R = 2,067×1016 с-1 Отсюда выразим Z , w=2pn=
, w=2pn= 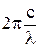 , откуда
, откуда
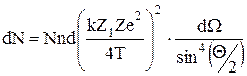
 т.е.
т.е.  (1)
(1) . (2)
. (2)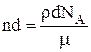 ,
, , 4pctg230=4573
, 4pctg230=4573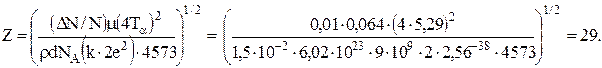

 . (1)
. (1) . (2)
. (2) (3)
(3)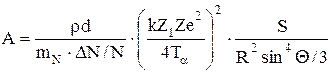 . (4)
. (4)
 , (2)
, (2)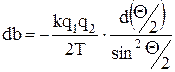 ; (3)
; (3) ; (4)
; (4) . (5)
. (5)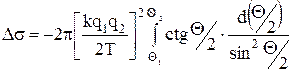 . (6)
. (6) ,
, : Ds= 2,1-10-26 м2.
: Ds= 2,1-10-26 м2.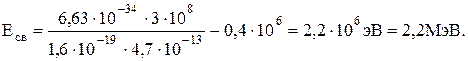
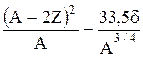 .
. .
. dM(Z)/dZ = 0.
dM(Z)/dZ = 0. = 0.
= 0. .
.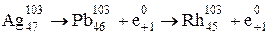 .
. Zmin=54.
Zmin=54. ведет к увеличению Z. Из этого следует, что оно обладает электронной активностью:
ведет к увеличению Z. Из этого следует, что оно обладает электронной активностью: .
. .
. .
. .
. . Результаты пояснить рисунком.
. Результаты пояснить рисунком.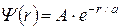 , где a = 0,53×10-10 м - радиус первой боровской орбиты, A - постоянная нормировки. Найти для основного состояния атома водорода наиболее вероятное расстояние электрона от ядра.
, где a = 0,53×10-10 м - радиус первой боровской орбиты, A - постоянная нормировки. Найти для основного состояния атома водорода наиболее вероятное расстояние электрона от ядра.