
|
|
Выписка из рабочей программы по физике (2000 г.)
Волновая оптика.Интерференция света. Когерентность и монохроматичность световых волн. Расчёт интерференционной картины от двух когерентных источников. Оптическая длина пути. Интерференция света в тонких пленках. Интерферометры. Дифракция света. Принцип Гюйгенса - Френеля. Метод зон Френеля. Прямолинейное распространение света. Дифракция Френеля на круглом отверстии и диске. Дифракция Фраунгофера на одной щели и дифракционной решетке. Разрешающая способность оптических приборов. Дифракция на пространственной решетке. Формула Вульфа-Брэгга. Принцип голографии. Исследование структуры кристаллов. Оптически неоднородная среда. Дисперсия света. Области нормальной и аномальной дисперсии. Электронная теория дисперсии света. Эффект Доплера. Излучение Вавилова-Черенкова. Поляризация света. Естественный и поляризованный свет. Поляризация света при отражении. Закон Брюстера. Двойное лучепреломление. Одноосные кристаллы. Поляроиды и поляризационные призмы. Закон Малюса. Квантовая природа излучения.Тепловое излучение. Черное тело. Закон Кирхгофа. Закон Стефана-Больцмана. Распределение энергии в спектре абсолютно черного тела. Закон смещения Вина. Квантовая гипотеза и формула Планка. Оптическая пирометрия. Внешний фотоэффект и его законы. Фотоны. Уравнение Эйнштейна для внешнего фотоэффекта. Масса и импульс фотона. Давление света. Опыты Лебедева. Квантовое и волновое объяснения давления света. Эффект Комптона и его теория.Диалектическое единство корпускулярных и волновых свойств электромагнитного излучения. Элементы атомной физики и квантовой механики.Опытное обоснование корпускулярно-волнового дуализма свойств вещества. Формула де Бройля. Соотношение неопределенностей как проявление корпускулярно-волнового дуализма свойств материи. Волновая функция и ее статистический смысл. Ограниченность механического детерминизма. Принцип причинности в квантовой механике.Стационарные состояния. Уравнение Шредингера для стационарных состояний.Свободная частица. Туннельный эффект. Частица в одномерной прямоугольной "потенциальной яме". Квантование энергии и импульса частицы. Понятие о линейном гармоническом осцилляторе. Атом водорода. Главное, орбитальное и магнитное квантовые числа. Опыт Штерна и Герлаха. Спин электрона. Спиновое квантовое число. Фермионы и бозоны. Принцип Паули. Распределение электронов в атоме по состояниям. Понятие об энергетических уровнях молекул. Спектры атомов и молекул. Поглощение, спонтанное и вынужденное излучения. Понятие о лазере. Элементы квантовой статистики и физики твердого тела. Фазовое пространство. Элементарная ячейка. Плотность состояний. Понятие о квантовой статистике Бозе - Эйнштейна. Фотонный и фононный газы. Распределение фононов по энергиям. Теплоемкость кристаллической решетки. Сверхтекучесть. Понятие о квантовой статистике Ферми - Дирака. Распределение электронов проводимости в металле по энергиям при абсолютном нуле температуры. Энергия Ферми. Влияние температуры на распределение электронов. Сверхпроводимость. Магнитные свойства сверхпроводников. Энергетические зоны в кристаллах. Распределение электронов по энергетическим зонам. Валентная зона и зона проводимости. Металлы, диэлектрики и полупроводники. Собственная проводимость полупроводников. Квазичастицы - электроны проводимости и дырки. Эффективная масса электрона в кристалле. Примесная проводимость полупроводников. Электронный и дырочный полупроводники. Контактные явления. Контакт электронного и дырочного полупроводника (p-n - переход) и его вольт-амперная характеристика. Фотоэлектрические явления в полупроводниках. Люминесценция твердых тел. Элементы физики атомного ядра и элементарных частиц. Заряд, размер и масса атомного ядра. Массовое и зарядовое числа. Момент импульса ядра и его магнитный момент. Состав ядра. Работы Иваненко и Гейзенберга. Нуклоны. Взаимодействие нуклонов и понятие о свойствах и природе ядерных сил. Дефект массы и энергия связи ядра. Закономерности и происхождение альфа-, бета-, и гамма-излучения атомных ядер. Ядерные реакции и законы сохранения. Реакция деления ядер. Цепная реакция деления. Понятие о ядерной энергетике. Реакция синтеза атомных ядер. Проблема управляемых термоядерных реакций. Элементарные частицы. Их классификация и взаимная превращаемость. Четыре типа фундаментальных взаимодействий: сильные, электромагнитные, слабые и гравитационные. Понятие об основных проблемах современной физики и астрофизики. СПИСОК ЛИТЕРАТУРЫ Основной 1. Савельев И.В. Курс общей физики. М.: Наука, 1988. Т.2, 3. 2. Сивухин Д.В. Общий курс физики. М.: Наука, 1980. Т.3, 4. 3. Детлаф А.А., Яворский Б.М., Милковская Л.Б. Курс физики. М.: Высшая школа, 1983. Т. 3. 478 с. 4. Трофимова Т.И. Курс физики. М.: Высшая школа, 1995. 472 с. 5. Чертов А.Г., Воробьев А.А. Задачник по физике. М.: Высшая школа, 1986. 496 с. 6. Воробьёв А.А. и др. Физика. Методические указания и контрольные задания/ Под ред. А.Г. Чертова. М.: Высшая школа, 1987. 208 с. 7. Волькенштейн В.С. Сборник задач по общему курсу физики. М.: Наука, 1988. 384 с. 8. Иродов И.Е. Задачи по общей физике. М.: Наука, 1991. 370 с. 9. Трофимова Т.И. Сборник задач по курсу физики. М.: Высшая школа, 1991. 303 с. Дополнительный 1. Матвеев А.Н. Механика и теория относительности. М.: Высшая школа, 1986. 208 с. 2. Епифанов Г.И., Мома Ю.А. Твердотельная электроника. М.: Высшая школа, 1986. 317 с. 3. Чертов А.Г. Единицы физических величин. М.: Высшая школа, 1977. 4. Диденко А.Я. , Филиппов В.П. Сборник задач по физике. Ч. 2. М.: ЦНИИатоминформ, 1992. 96 с. ОСНОВНЫЕ ПОНЯТИЯ, ЗАКОНЫ, ФОРМУЛЫ И ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО РАЗДЕЛАМ
ОПТИКА Скорость света в среде v = c/n, где с - скорость света в вакууме; n - абсолютный показатель преломления среды. Оптическая длина пути световой волны L = nl, где l - геометрическая длина пути световой волны в среде с абсолютнымпоказателем преломления n. Оптическая разность хода двух световых волн D= L1 - L2. Зависимость разности фаз от оптической разности хода световых волн Dj= 2p(D/l), где l - длина световой волны. Условие максимального усиления света при интерференции D = +kl (k = 0, 1, 2, ...) Условие максимального ослабления света D= ±(2k+1)×l/2. Оптическая разность хода световых волн, возникающая при отражении монохроматического света от тонкой пленки
где d - толщина пленки; n - показатель преломления пленки; i1 -угол падения; i2 - угол преломлениясвета в пленке. Радиус светлых колец Ньютона в отраженном свете
где k - номер кольца; R - радиус кривизны линзы. Радиус тёмных колец Ньютона в отражённом свете
Угол j отклонения лучей при нормальном падении, соответствующий максимуму при дифракции на дифракционной решётке, определяется из условия d×sinj = ± kl (k = 1, 2, 3...,kmax), где d - период дифракционной решётки. Разрешающая способность дифракционной решётки R = l/Dl = k×N, где Dl - наименьшая разность длин волн двух соседних спектральных линий (l и l + Dl), при которой эти линии могут быть видны раздельно в спектре, полученном посредством данной решётки; N - полное число щелей решётки. Формула Вульфа - Брэггов 2d×sinq = k×l ( k = 1, 2, 3..., kmax), где q - угол скольжения (угол между направлением параллельного пучка рентгеновского излучения, падающего на поверхность кристалла, и атомной плоскостью в кристалле); d - расстояние между атомными плоскостями . Закон Брюстера tgib = n21, где ib - угол падения, при котором отразившийся от диэлектрика луч полностью поляризован; n21 - относительный показатель преломления второй среды относительно первой. Закон Малюса I = I0cos2a, где I0 - интенсивность плоскополяризованного света, падающего на анализатор; I - интенсивность света, прошедшего через анализатор; a - угол между направлением колебаний электрического вектора света, падающего на анализатор, и плоскостью пропускания анализатора. Степень поляризации света
где Imax и Imin - максимальная и минимальная интенсивности частично поляризованного света, пропускаемого анализатором. Угол поворота плоскости поляризации монохроматического света при прохождении через оптически активное вещество: а) j = a×d (в твёрдых телах), где a- постоянная вращения; d - длина пути, пройденного светом в оптически активном веществе; б) j = [a]rd (в растворах), где [a] - постоянная вращения; d - длина пути, пройденного светом в оптически активном веществе; r- массовая концентрация оптически активного вещества в растворе. Релятивистская масса
Энергия релятивистской частицы
где Eo = moc2 - энергия покоя частицы; b = v/c. Полная энергия свободной частицы E = Eo + T, где T - кинетическая энергия релятивистской частицы. Кинетическая энергия релятивистской частицы E=(m - m0)c2 или Импульс релятивистской частицы
Связь между полной энергией и импульсом релятивистской частицы E2 = Eo2 + (pc)2. Эффект Доплера в релятивистском случае n = no×(1 + bcosq)/(1 - b2)1/2, где n - частота света, воспринимаемого наблюдателем; no - собственная частота излучения, испускаемого неподвижным источником; b = v/c; v - скорость источника излучения относительно наблюдателя, c - скорость света в вакууме; q - угол между векторомv и направлением наблюдения, измеренный в системе отсчёта, связанной с наблюдателем. При движении источника вдоль прямой, соединяющей наблюдателя и источник, возможны два случая: а) источник удаляется от наблюдателя (q= 0): n = no[(1 + b)/(1 - b)]1/2, б) источник приближается к наблюдателю (q = p): n = no[(1 - b)/(1 + b)]1/2. Закон Стефана - Больцмана Re = s×T4, где Re - энергетическая светимость (излучательность) абсолютно чёрного тела; s - постоянная Стефана - Больцмана; T - термодинамическая температура. Закон смещения Вина lm = b/T, где lm - длина волны, на которую приходится максимум спектральной плотности энергии излучения; b - постоянная Вина. Энергия фотона e= hn или e = ħw, где h - постоянная Планка; n - частота фотона; w - циклическая частота; ħ = h/2p. Масса фотона m = e/c2 = h/(cl), где c - скорость света в вакууме; l - длина волны фотона. Импульс фотона p = mc = h/l. Формула Эйнштейна для внешнего фотоэффекта hn = A + Tmax = где hn - энергия фотона, падающего на поверхность металла; A - работа выхода электрона; Tmax - максимальная кинетическая энергия электрона, покинувшего металл. Красная граница фотоэффекта no = A/h или lo = hc/A, где no - минимальная частота света, при которой ещё возможен фотоэффект; lo - максимальная длина волны, при которой ещё возможен фотоэффект; h - постоянная Планка; c - скорость света в вакууме. Формула Комптона
где l - длина волны фотона, встретившегося со свободным или слабо связанным электроном; l2 - длина волны фотона, рассеянного на угол q после столкновения с электроном; mo - масса покоящегося электрона. Давление света при нормальном падении на поверхность p = Ee(1 + r)/c = w(1+ r), где Ee - энергетическая освещённость (облучённость); w - объёмная плотность энергии излучения; r - коэффициент отражения.
Примеры решения задач Пример 1. От двух когерентных источников S1 и S2 (l = 0.8 мкм) лучи попадают на экран. На экране наблюдается интерференционная картина. Когда на пути одного из лучей перпендикулярно ему поместили мыльную пленку (n = 1.33), интерференционная картина изменилась на противоположную. При какой наименьшей толщине dmin пленки это возможно? Решение. Изменение интерференционной картины на противоположную означает, что на тех участках экрана, где наблюдались интерференционные максимумы, стали наблюдаться интерференционные минимумы. Такой сдвиг интерференционной картины возможен при изменении оптической разности хода пучков световых волн на нечетное число половин длин волн, т.е. D2 - D1 = (2k+1)l/2, (1) где D1 - оптическая разность хода пучков световых волн до внесения пленки; D2 - оптическая разность хода тех же пучков после внесения пленки; k = 0, +1, +2, ...,+kmax. Наименьшей толщине dmin пленки соответствует k = 0. При этом формула (1) примет вид D2 - D1 = l/2. (2) Выразим оптические разности хода D2 и D1: D1 = l1 - l2, D2 = [(l1 - dmin)+n×dmin] - l2 = (l1-l2) + dmin(n-1). Подставим выражения D1 и D2 в формулу (2): (l1-l2) + dmin(n-1) - (l1-l2) = l/2. или dmin(n-1) = l/2. Отсюда dmin = l/[2(n-1)]. Произведем вычисления:
Пример 2. Определить импульс p и кинетическую энергию T электрона, движущегося со скоростью v = 0,9 c, где c - скорость света в вакууме. Решение. Импульсом частицы называется произведение массы частицы на её скорость: p = mv. (1) Так как скорость электрона близка к скорости света, то необходимо учесть зависимость массы от скорости, определяемую по формуле
где m - масса движущейся частицы; mo - масса покоящейся частицы; b = v/c - скорость частицы, выраженная в долях скорости света. Заменив в формуле (1) массу m её выражением (2) и приняв во внимание, что v = cb, получим выражение для релятивистского импульса:
Произведём вычисления: p = 9,31×10-31×0,9×3×103/ В релятивистской механике кинетическая энергия T частицы определяется как разность между полной энергией и энергией покоя Eo этой частицы, т.е. T = E - Eo. Так как E = mc2 и Eo = moc2, то учитывая зависимость массы от скорости, получаем:
Произведём вычисления:
Пример 3. Длина волны, на которую приходится максимум энергии в спектре излучения черного тела, lmax = 0,58 мкм. Определить энергетическую светимость Re поверхности тела. Решение. Энергетическая светимость Re абсолютно чёрного тела в соответствии с законом Стефана - Больцмана пропорциональна четвёртой степени термодинамической температуры и выражается формулой Re = sT4, (1) где s- постоянная Стефана - Больцмана; T -абсолютная температура. Температуру T - можно вычислить с помощью закона смещения Вина: lo = b/T, (2) где b - постоянная закона смещения Вина. Используя формулы (2) и (1), получаем Re = s(b/l)4. (3) Произведём вычисления: Re = 5,67×10-8×(2,9×10-3/5,8×10-7)4 = 3,54×107 Вт/м2.
Пример 4. Определить максимальную скорость vmax фотоэлектронов, вырываемых с поверхности серебра: 1) ультрафиолетовым излучением с длиной волны l1 = 0,155 мкм; 2) g - излучением с длиной волны l2 = 1 пм. Решение. Максимальную скорость фотоэлектронов можно определить из уравнения Эйнштейна для внешнего фотоэффекта: e = A + Tmax, (1) где e - энергия фотонов, падающих на поверхность металла; A - работа выхода; Tmax - максимальная кинетическая энергия фотоэлектронов. Энергию фотона можно вычислить по формуле: e= hc/l, (2) где h - постоянная Планка; c - скорость света в вакууме; l - длина волны. Кинетическая энергия электрона может быть выражена или по классической формуле T = mov2/2, (3) или по релятивистской формуле
в зависимости от того, какая скорость сообщается фотоэлектрону. Скорость фотоэлектрона зависит от энергии фотона, вызывающего фотоэффект; если энергия e фотона много меньше энергии покоя Eo электрона, то может быть применена формула (3), если же e сравнима с Eo, то вычисление по формуле (3) приводит к ошибке, поэтому нужно пользоваться формулой (4). 1. Вычислим энергию фотона ультрафиолетового излучения по формуле (2): e1 = 6,63×10-34×3×108/1,55×10-7 = 1,28×10-18 Дж или e1 = 1,28×10-18/1,6×10-19 = 8 эВ. Полученная энергия фотона e1 < Eo (Eo = 0,51 МэВ - энергия покоя электрона). Следовательно, в данном случае кинетическая энергия фотоэлектрона в формуле (1) может быть выражена по классической формуле (3): e1 = A + mov2max/2. откуда
Подставив значения величин в формулу (5), найдём vmax= Вычислим энергию фотона g - излучения: e2 = hc/l = 6,63×10-34×3×108/1×1012 = 1,99×10-13 Дж, или во внесистемных единицах e2 = 1,99×10-13/1,6×10-19 = 1,24×106 эВ = 1,24 МэВ. Работа выхода электрона (A = 4,7 эВ) пренебрежимо мала по сравнению с энергией фотона (e2 = 1,24 МэВ), поэтому можно принять, что максимальная кинетическая энергия электрона равна энергии фотона: Tmax = 1,24 МэВ. Так как в данном случае кинетическая энергия электрона больше его энергии покоя, то для вычисления скорости электрона следует взять релятивистскую формулу кинетической энергии (4). Из этой формулы найдём
Заметив, что v = cb и Tmax = e2, получим
Произведём вычисления:
Пример 5. В результате эффекта Комптона фотон при соударении с электроном был рассеян на угол q = 90o. Энергия рассеянного фотона e2 = 0,4 МэВ. Определить энергию фотона e1 до рассеяния. Решение. Для определения энергии первичного фотона воспользуемся формулой Комптона:
где Dl = l2 - l1 - изменение длины волны фотона в результате рассеяния на свободном электроне; h - постоянная Планка; mo – масса покоя электрона; c - скорость света в вакууме; q- угол рассеяния фотона. Преобразуем формулу (1): 1) заменим в ней Dl на l2 - l1; 2) выразим длины волн l1 и l2 через энергии e1 и e2 соответствующих фотонов, воспользовавшись формулой e = hc/l; 3) умножим числитель и знаменатель правой части формулы на c, тогда
Сократим на hc и выразим из этой формулы искомую энергию:
где Eo = moc2 - энергия покоя электрона. Вычисления по формуле (2) удобнее вести во внесистемных единицах. Так как для электрона Eo = 0,511 МэВ, то e1 = 0,4×0,511/(0,511 - 2×0,4×sin245o) = 1,85 МэВ.
Пример 6. Пучок монохроматического света с длиной волны l = 663 нм падает на зеркальную плоскую поверхность. Поток излучения Фe = 0,6 Вт. Определить 1) силу давления F, испытываемую этой поверхностью; 2) число фотонов ежесекундно падающих на поверхность. Решение. 1. Сила светового давления на поверхность равна произведению светового давления p на площадь S поверхности: F = pS. (1) Световое давление может быть найдено по формуле: p = Ee(r + 1)/c, (2) где Ee - энергетическая освещённость поверхности; c - скорость света в вакууме; r - коэффициент отражения. Подставляя правую часть выражения (2) в формулу (1), получаем F = EeS(r + 1)/с. (3) Так как EeS представляет собой поток излучения Фe, то F = Фe(r + 1)/c. (4) Произведём вычисления, учитывая, что для зеркальной поверхности r=1: F = 0,6(1 + 1)/3×108 = 4 нН. 2. Произведение энергии e одного фотона на число фотонов n1, ежесекундно падающих на поверхность, равно мощности излучения, т.е. потоку излучения: Фe = e×n1, а так как энергия фотона e == hc/l, то Фe = h×c×n1l, откуда n1 = Фel/(hc). (5) Произведём вычисления: n1 = 0,6×6,63×10-7/(6,63×10-34×3×108) = 2×1018 с-1.
КОНТРОЛЬНАЯ РАБОТА 5
Таблица вариантов
1. В интерферометре Майкельсона на пути одного из интерферирующих пучков света (l=590 нм) поместили закрытую с обеих сторон стеклянную трубку длиной l = 10 см, откачанную до высокого вакуума. При заполнении трубки хлористым водородом произошло смещение интерференционной картины. Когда хлористый водород был заменен бромистым водородом, смещение интерференционной картины возросло на m = 42 полосы. Определить разность n показателей преломления бромистого и хлористого водорода. 2. На мыльную пленку (n=1,3), находящуюся в воздухе, падает нормально пучок лучей белого света. При какой наименьшей толщине d пленки отраженный свет с длиной волны l=0,55 мкм окажется максимально ослабленным вследствие интерференции? 3. Пучок монохроматических (l=0,6 мкм) световых волн падает под углом i=300 на находящуюся в воздухе мыльную пленку (n=1,3). При какой наименьшей толщине d пленки отраженные световые волны будут максимально ослаблены интерференцией? 4. На тонкий стеклянный клин (n=1,55) падает нормально монохромати-ческий свет. Двугранный угол a между поверхностями клина равен 2'. Определить длину световой волны l, если расстояние b между смежными интерференционными максимумами в отраженном свете равно 0,3 мм. 5. Поверхности стеклянного клина образуют между собой угол a=0,2'. На клин нормально к его поверхности падает пучок лучей монохроматического света с длиной волны l=0,55 мкм. Определить ширину b интерференционной полосы. 6. На тонкий стеклянный клин в направлении нормали к его поверхности падает монохроматический свет (l=600 нм). Определить угол a между поверхностями клина, если расстояние b между смежными интерференционными минимумами в отраженном свете равно 4 мм. 7. На тонкую плёнку (n = 1,33) падает параллельный пучок белого света. Угол падения q1 = 520. При какой толщине плёнки зеркально отражённый свет будет наиболее сильно окрашен в жёлтый цвет (l = 0,60 мкм)? 8. На пути световой волны, идущей в воздухе, поставили стеклянную пластинку толщиной h= 1 мм. На сколько изменится оптическая длина пути, если волна падает на пластинку: 1) нормально; 2) под углом j=30o? 9. На пути монохроматического света с длиной волны l=0,6 мкм находится плоскопараллельная стеклянная пластина толщиной d=0,1 мм. Свет падает на пластину нормально. На какой угол j следует повернуть пластину, чтобы оптическая длина пути L изменилась на l/2? 10. Найти все длины волн видимого света (от 0,76 до 0,38 мкм), которые будут: 1) максимально усилены; 2) максимально ослаблены при оптической разности хода l волн, равной 1,8 мкм. 11. Плоская монохроматическая световая волна падает нормально на диафрагму с двумя узкими щелями, отстоящими друг от друга на расстояние d = 100 см, образуя систему интерференционных полос. На какое расстояние сместятся эти полосы, если одну из щелей перекрыть стеклянной пластинкой толщины h = 10 мм? 12. Расстояние d между двумя щелями в опыте Юнга равно 1 мм, расстояние L от щелей до экрана равно 3 м. Определить длину волны l, испускаемой источником монохроматического света, если ширина b полос интерференции на экране равна 1,5 мм. 13. В опыте с зеркалами Френеля расстояние d между мнимыми изображениями источника света равно 0.5 мм, расстояние L от них до экрана равно 3 м. Длина волны l=0,6 мкм. Определить ширину b полос интерференции на экране. 14. Между двумя плоскопараллельными стеклянными пластинками положили очень тонкую проволочку, расположенную параллельно линии соприкосновения пластинок и находящуюся на расстоянии l=75 мм от нее. В отраженном свете (l = 0,5 мкм) на верхней пластинке видны интерференционные полосы. Определить диаметр d поперечного сечения проволочки, если на протяжении a=30 мм насчитывается N=16 светлых полос. 15. Две плоскопараллельные стеклянные пластинки приложены одна к другой так, что между ними образовался воздушный клин с углом a, равным 30". На одну из пластинок падает нормально монохроматический свет (l=0,6 мкм). На каких расстояниях l1 и l2 от линии соприкосновения пластинок будут наблюдаться в отраженном свете первая и вторая светлые полосы (интерференционные максимумы)? 16. Диаметр d2 второго светлого кольца Ньютона при наблюдении в отраженном свете (l = 0,6 мкм) равен 1,2 мм. Определить оптическую силу D плосковыпуклой линзы, взятой для опыта. 17. Плосковыпуклая линза с оптической силой Ф=2 дптр выпуклой стороной лежит на стеклянной пластинке. Радиус r4 четвертого темного кольца Ньютона в проходящем свете равен 0,7 мм. Определить длину световой волны. 18. Между стеклянной пластинкой и лежащей на ней плосковыпуклой стеклянной линзой налита жидкость, показатель преломления которой меньше показателя преломления стекла. Радиус r8 восьмого темного кольца Ньютона при наблюдении в отраженном свете (l=700 нм) равен 2 мм, радиус R кривизны выпуклой поверхности линзы равен 1 м. Найти показатель преломления n жидкости. 19. На установке для наблюдения колец Ньютона был измерен в отраженном свете радиус третьего темного кольца (k=3). Когда пространство между плоскопараллельной пластиной и линзой заполнили жидкостью, то тот же радиус стало иметь кольцо с номером, на единицу большим. Определить показатель преломления n жидкости. 20. Две плоскопараллельные стеклянные пластинки образуют клин с углом a=30'. Пространство между пластинками заполнено глицерином. На клин нормально к его поверхности падает пучок монохроматического света с длиной волны l = 500 нм. В отраженном свете наблюдается интерференционная картина. Какое число N темных интерференционных полос приходится на 1 см длины клина? 21. Расстояние между вторым и первым темным кольцами Ньютона в отраженном свете равно 1 мм. Определить расстояние Dr9,10 между десятым и девятым кольцами. 22. Расстояние от бипризмы Френеля до узкой щели и экрана равны соответственно a = 25 см и b = 100 см. Бипризма стеклянная с преломляющим углом q = 20'. Найти длину волны, если ширина интерференционной полосы на экране Dx = 0,55 мм. 23. Кольца Ньютона наблюдаются с помощью двух одинаковых плоско-выпуклых линз радиусом R кривизны равным 1 м, сложенных вплотную выпуклыми поверхностями (плоские поверхности линз параллельны). Определить радиус r2 второго светлого кольца, наблюдаемого в отраженном свете (l=660 нм) при нормальном падении света на поверхность верхней линзы. 24. Определить перемещение зеркала в интерферометре Майкельсона, если интерференционная картина сместилась на m=100 полос. Опыт проводился со светом с длиной волны l=546 нм. 25. В установке для наблюдения колец Ньютона свет с длиной волны l=0,5 мкм падает нормально на плосковыпуклую линзу с радиусом кривизны R1=1 м, положенную выпуклой стороной на вогнутую поверхность плосковогнутой линзы с радиусом кривизны R2=2 м. Определить радиус r3 третьего темного кольца Ньютона, наблюдаемого в отраженном свете. 26. На дифракционную решетку нормально к поверхности падает монохроматический свет (l=650 нм). За решеткой находится линза, в фокальной плоскости которой расположен экран. На экране наблюдается дифракционная картина под углом дифракции j = 30o. При каком главном фокусном расстоянии F линзы линейная дисперсия Dl=0,5 мм/нм. 27. На грань кристалла каменной соли падает параллельный пучок рентгеновского излучения (l=147 пм). Определить расстояние d между атомными плоскостями кристалла, если дифракционный максимум второго порядка наблюдается, когда излучение падает под углом j=31o30' к поверхности кристалла. 28. Плоская световая волна (l = 0,5 мкм) падает нормально на диафрагму с круглым отверстием диаметром d=1 см. На каком расстоянии b от отверстия должна находиться точка наблюдения, чтобы отверстие открывало: 1) одну зону Френеля? 2) две зоны Френеля? 29. Свет с длиной волны 535 нм падает нормально на дифракционную решётку. Найти её период, если одному из фраунгоферовых максимумов соответствует угол дифракции 35o и наибольший порядок спектра равен пяти. 30. Плоская световая волна (l=0,7 мкм) падает нормально на диафрагму с круглым отверстием радиусом r=1,4 мм. Определить расстояния b1, b2, b3 от диафрагмы до трех наиболее удаленных от нее точек, в которых наблюдаются минимумы интенсивности. 31. Вычислить радиус r5 пятой зоны Френеля для плоского волнового фронта (l=0,5 мкм), если построение делается для точки наблюдения, находящейся на расстоянии b=1 м от фронта волны. 32. Радиус r4 четвертой зоны Френеля для плоского волнового фронта равен 3 мм. Определить радиус r6 шестой зоны Френеля. 33. На диафрагму с круглым отверстием диаметром d=4 мм падает нормально параллельный пучок лучей монохроматического света (l = 0,5 мкм). Точка наблюдения находится на оси отверстия на расстоянии b=1 м от него. Сколько зон Френеля укладывается в отверстии? Темное или светлое пятно получится в центре дифракционной картины, если в месте наблюдений поместить экран? 34. Сколько штрихов на каждый миллиметр содержит дифракционная решетка, если при наблюдении в монохроматическом свете с длиной волны l=0,6 мкм максимум пятого порядка отклонен на угол j=180? 35. На дифракционную решетку, содержащую n = 100 штрихов на 1 мм, падает нормально монохроматический свет. Зрительная труба спектрометра наведена на максимум третьего порядка. Чтобы навести трубу на другой максимум того же порядка, ее нужно повернуть на угол j1=200. Определить длину волны l света. 36.Дифракционная решетка освещена нормально падающим монохроматическим светом. В дифракционной картине максимум второго порядка отклонен на угол j1=140. На какой угол j2 отклонен максимум третьего порядка? 37. Дифракционная решетка содержит n=200 штрихов на 1 мм. На решетку падает нормально монохроматический свет (l = 0,6 мкм). Максимум какого наибольшего порядка дает эта решетка? 38. На дифракционную решетку, содержащую n = 400 штрихов на 1 мм, падает нормально монохроматический свет (l=0,6 мкм). Найти общее число дифракционных максимумов, которые дает эта решетка. Определить угол j дифракции, соответствующий последнему максимуму. 39. На щель шириной а = 0,05 мм падает нормально монохроматический свет (l=0,6 мкм). Определить угол j между первоначальным направлением пучка света и направлением на четвертую темную дифракционную полосу. 40. На узкую щель падает нормально монохроматический свет. Угол отклонения пучков света, соответствующих второй светлой дифракционной полосе, равен 10 . Скольким длинам волн падающего света равна ширина щели? 41. На щель шириной a= 0,1 мм падает нормально монохроматический свет (l=0,5 мкм). За щелью помещена собирающая линза, в фокальной плоскости которой находится экран. Что будет наблюдаться на экране, если угол j дифракции равен: 1) 17', 2) 43'. 42. Дифракционная картина получена с помощью дифракционной решетки длиной l=1,5 см и периодом d=5 мкм. Определить, в спектре какого наименьшего порядка этой картины получатся раздельные изображения двух спектральных линий с разностью длин волн Dl=0,1 нм, если линии лежат в крайней красной части спектра (l ~ 760 нм). 43. Какой наименьшей разрешающей силой R должна обладать дифракционная решетка, чтобы с ее помощью можно было разрешить две спектральные линии калия (l1=578 нм и l2=580 нм)? Какое наименьшее число N штрихов должна иметь эта решетка, чтобы разрешение было возможно в спектре второго порядка? 44. С помощью дифракционной решетки с периодом d=20 мкм требуется разрешить дублет натрия (l1 = 589,0 нм и l2 = 589,6 нм) в спектре второго порядка. При какой наименьшей длине l решетки это возможно? 45. Угловая дисперсия D дифракционной решетки для излучения некоторой длины волны (при малых углах дифракции) составляет 5 мин/нм. Определить разрешающую силу R этой решетки для излучения той же длины волны, если длина l решетки равна 2 см. 46. Определить угловую дисперсию D дифракционной решетки для угла дифракции j = 300 и длины волны l = 600 нм. Ответ выразить в единицах СИ. 47. На дифракционную решетку, содержащую n = 500 штрихов на 1 мм, падает нормально монохроматический свет с длиной волны , равной 700 нм. За решеткой помещена собирающая линза с главным фокусным расстоянием F=50 см. В фокальной плоскости линзы расположен экран. Определить линейную дисперсию Dl такой системы для максимума третьего порядка. Ответ выразить в миллиметрах на нанометр. 48. При освещении дифракционной решетки белым светом спектры второго и третьего порядков отчасти перекрывают друг друга. На какую длину волны в спектре второго порядка накладывается фиолетовая граница (l = 0,4 мкм) спектра третьего порядка? 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , или D = 2d×n×cosi2 ± l/2,
, или D = 2d×n×cosi2 ± l/2, , (k = 1, 2, 3,...),
, (k = 1, 2, 3,...), .
. ,
,


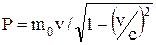
 ,
, или
или  ,
, = 1,21 мкм.
= 1,21 мкм.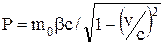 . (3)
. (3)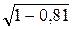 =5,6×10-23 кг×м/с.
=5,6×10-23 кг×м/с. . (4)
. (4) .
. , (4)
, (4)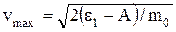 . (5)
. (5) .
.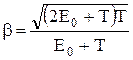 .
. .
. .
.
 (2)
(2)