
|
|
Кристаллические решетки. ИНДЕКСЫ МИЛЛЕРАМАТЕРИАЛОВЕДЕНИЕ
Методические указания к практическим занятиям
Волгоград УДК 620.1.: 669.1
Рецензент: канд. техн. наук доцент В. Н. Тышкевич
Издается по решению редакционно-издательского совета Волгоградского государственного технического университета
Носенко, В.А. Материаловедение [Электронный ресурс]: методические указания к практическим занятиям / В.А. Носенко, Т.С. Тарасова, О.М. Ладыгина // Сборник «Методические указания» Выпуск 3. - Электрон. текстовые дан. (1 файл: 3,73 МБ) – Волжский: ВПИ (филиал) ВолгГТУ, 2015. - Систем. требования: Windows 95 и выше; ПК с процессором 486+; CD-ROM.
В методических указаниях представлен теоретический материал для решения задач на практических занятиях по дисциплине «Материаловедение» с примерами их выполнения. Предназначены для студентов высших учебных заведений, обучающихся по направлениям подготовки бакалавров: «Конструкторско-технологическое обеспечение машиностроительных производств»; «Стандартизация и метрология»; «Автоматизация технологических процессов и производств (по отраслям)»; «Эксплуатация транспортно-технологических машин и комплексов»; «Энерго- и ресурсосберегающие процессы в химической технологии, нефтехимии и биотехнологии».
Ó Волгоградский государственный технический университет, 2015 Ó Волжский политехнический институт, 2015
СОДЕРЖАНИЕ
ВВЕДЕНИЕ
Практические занятия проводятся с целью более полного изучения теоретического лекционного материала по дисциплине «Материаловедение». На занятиях рассматриваются конкретные примеры, проводятся расчеты и графические построения под руководством преподавателя, затем выполняются самостоятельно задачи, которые оцениваются методикой рейтингового контроля. Каждое практическое занятие имеет продолжительность два академических часа. Если студент не успел выполнить самостоятельное задание, то он обязан представить его преподавателю на следующее занятие для оценки. Темы практических занятий: 1 Кристаллические решетки. Индексы Миллера. 2 Термический метод анализа металлов и сплавов. Построение кривых охлаждения и диаграмм состояния двойных сплавов. Правило фаз (закон Гиббса). 3 Правило отрезков. 4 Изучение диаграмм состояния двойных сплавов. 5 Системы с тремя компонентами. 6 Диаграмма состояния железоуглеродистых сплавов. 7 Термическая обработка. Определение оптимального режима закалки углеродистой стали. 8 Оценка качества термической обработки по определению размеров аустенитных зерен.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 1 Кристаллические решетки. ИНДЕКСЫ МИЛЛЕРА
Атомы в кристаллическом твердом теле располагаются в пространстве закономерно, периодически повторяясь в трех измерениях через строго определенные расстояния, то есть образуют кристаллическую решетку. Кристаллическую решетку можно «построить» выбрав для этого определенный «строительный блок» (аналогично постройки стены из кирпичей) и многократно смещая этот блок по трем направлениям. Такая «строительная единица» называется элементарной ячейкой. Все элементарные ячейки, составляющие кристаллическую ячейку, имеют одинаковую форму и объемы. Атомы могут располагаться как в вершинах элементарной ячейки, так и в других ее точках (узлах кристаллической решетки). В первом случае элементарные ячейки называют простыми (примитивными), во втором – сложными. Если форма элементарной ячейки определена и известно расположение всех атомов внутри нее, то имеется полное геометрическое описание кристалла, т.е. известна ее атомно-кристаллическая структура. В кристаллографии рассматривают 14 типов элементарных ячеек. Их называют пространственными решетками Бравэ. Для характеристики элементарной ячейки задают шесть величин: три ребра ячейки а, в, с, измеряемые в ангстремах
Рис. 1. Параметры элементарной ячейки
Все 14 решеток расположены по семи кристаллическим системам (сингониям). Каждая сингония включает одну или несколько типов пространственных кристаллических решеток. В простой решетке - атомы располагаются только по вершинам решетки. В объемноцентрированной -еще один атом в центре решетки. В гранецентрированной - еще по одному атому в центре каждой грани, в базоцентрированной еще по одному атому в центрах двух оснований (табл. 1). Узлы (положение атомов), направления в плоскости и пространстве обозначаются с помощью индексов Миллера. 1 Положение любого узла кристаллической решетки относительно произвольно выбранного начала координат определяют заданием координат x, y, z. Для одной элементарной ячейки очевидно эти координаты равны параметрам решетки а, в, с соответственно. Для удаленной от начала координат ячейки координаты узла определяются как х=ma, y=nв, z=рс, где m, n, р – целые числа. Если за единицу измерения длин вдоль осей решетки выбрать величины а, в, с, то координаты узла будут числа m, n, р. Они называются индексами узлаи записываются [[mnр]]. Для отрицательных индексов узла (отрицательные значения m, n, р) над индексом ставится знак «-». Например: для узла с координатами х=3a, y=1в, z=4с индексы равны [[314]]; для узла с координатами х=-1a, y=1в, z=-2с индексы равны Таблица 1
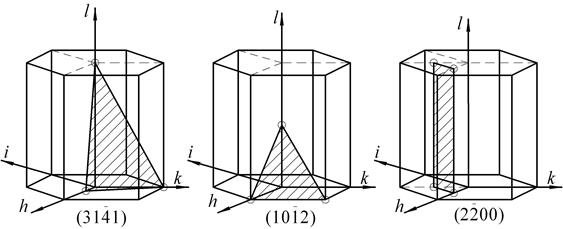
2 Индексы направления определяются индексами первого узла, через который проходит прямая, проведенная от начала координат, поэтому индексы направления, обозначаемые как [mnр] численно равны индексам узла [[mnр]]. 3 Положение плоскости определяется отрезками А, В, С, которые она отсекает на осях решетки. Далее определяются величины обратные им 1/А, 1/В, 1/С. если плоскость не пересекает какую-нибудь ось, то соответствующий индекс Миллера равен нулю. Положение плоскости записывается в скобках. Наиболее распространенными среди металлов являются решетки: ГПУ - гексагональная плотноупакованная; ГЦК – гранецентрированная кубическая; ОЦК – объемноцентрированная кубическая (рис. 2).
а Рис. 2. Кристаллические решетки: а – ГПУ; б – ГЦК; в – ОЦК
Для описания кристаллов с гексагональной решеткой пользуются четырехосной системой координат (в основании призмы лежат три оси под углом 120°, а четвертая ось перпендикулярна им). В этом случае плоскость обозначается (h k i l), где
Рис. 3. Гексагональная решетка Координационное число решетки (к) – число атомов, находящихся на равном расстоянии от данного атома. В кристалле из одинаковых атомов максимальное значение к=12. Так, кубическая примитивная решетка имеет к=6, у ОЦК к=8, у ГЦК к=12. Для изучения структур кристаллов важное значение имеет относительная плотность упаковки – доля объема, занятая атомами по сравнению со всем объемом кристалла. Плотность упаковки (компактность) примитивной кубической решетки - 0,52, решетки ОЦК – 0,67, решетки ГЦК – 0,74. Компактность структуры является одним из факторов, уменьшающих свободную энергию твердого тела, то есть обеспечивающих его равновесное состояние. ЗАДАЧА № 1Изобразите индексы узлов, направлений, плоскости для гексагональной и кубической решетки.
Рис. 4. Положение плоскостей в гексагональной решетке
Рис. 5. Индексы узлов, направлений, положение плоскостей в кубической решетке
ЗАДАЧА № 2 1 Изобразите индексы узлов, направлений, плоскости для ромбической решетки с размерами 2 Изобразите плоскости гексагональной решетки (1011), 3 Плоскость пересекает оси координат в точках 1/3а, 1/2в, 1с. Каковы индексы этой плоскости? 4 Как проходит через элементарную ячейку плоскость (231)? 5 Напишите индексы направлений ok, оn (рис. 4).
Практическое занятие № 2 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|


 и три угла между ними a, b, g (рис. 1). Эти величины называют параметрами элементарной ячейки.
и три угла между ними a, b, g (рис. 1). Эти величины называют параметрами элементарной ячейки.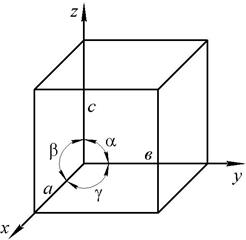
 .
. б
б  в
в 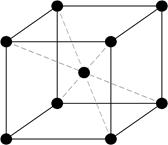
 (рис. 2).
(рис. 2).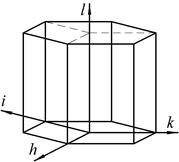

 ,
,  ,
,  :
:  ,
,  ,
,  ,
,  , (310),
, (310),  .
. ,
,  .
.