
|
|
Определение потерь напора по длине
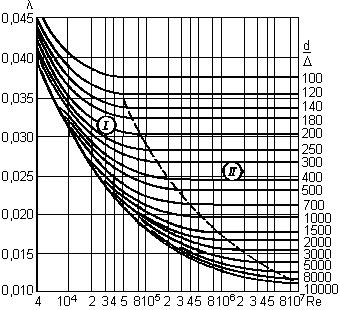
III. Турбулентный режим III.1. Область гладких русел 4000 Формула Блазиуса Формула Прандтля III.2. Доквадратичная область С увеличением числа Формула Альтшуля Формула Кольбрука
III.3. Квадратичная область И, наконец, при больших числах Формула Прандтля Формула Шифринсона
Местные потери напора Местные потери напора - это потери, обусловленные местными гидравлическими сопротивлениями, то есть такими элементами трубопроводов, в которых вследствие изменения поперечных размеров или конфигурации происходит деформация потока. Всякая перестройка структуры потока связанная с появлением дополнительных касательных напряжений, причиной которых являются возникающие в потоке дополнительные вихреобразования. Местные потери энергии имеют ту же физическую природу, что и потери по длине - это результат преобразования части механической энергии в тепловую за счет преодоления касательных напряжений трения. Основные виды местных потерь напора можно условно подразделить на ряд групп, соответствующих определенным видам местных сопротивлений:
Общим для всех видов местных сопротивлений является:
Местные потери напора определяются по формуле Вейсбаха
где Коэффициент местного сопротивления зависит в основном от формы местного сопротивления и его геометрических размеров. Теоретически достаточно точно коэффициент местного сопротивления при турбулентном режиме движения можно определить для внезапного расширения, когда труба диаметром
Обозначим давление, скорость и площадь потока в сечении 1-1 через Запишем для данных сечений уравнение Бернулли, с учетом, что
Тогда
Изменение количества движения отсека жидкости между сечениями 1-1 и 2-2 равно импульсу сил действующих на этот отсек. Проекция на ось X изменение количества движения определяется по формуле
Исходя из ранее принятого допущения, на рассматриваемый отсек жидкости действуют только силы гидродинамического давления, проектируемые на ось X
Разделим левую и правую части уравнения на
После преобразования окончательно имеем
Формула называется формулой Борда. Согласно ей потери напора при внезапном расширении равны скоростному напору потерянной скорости, так как разность Выражение можно привести к другому виду. Выразим первую скорость через вторую, используя уравнение расхода
Тогда
Обозначив
где Окончательно получим
Формула может быть преобразована, если выразить вторую скорость через первую
Обозначив
Окончательно получим
пренебрежимо малы по сравнению с потерями напора на участке расширения (от Поэтому потери напора при входном сужении могут быть найдены по формуле Борда
Из уравнения неразрывности потока определим
Используя понятие коэффициента сжатия струи
Обозначив
Окончательно получим
где Коэффициент сжатия струи Значение Как показали экспериментальные исследования, коэффициент местного сопротивления зависит не только от вида самого местного сопротивления, но и от режима движения жидкости, то есть от числа Рейнольдса Эти значения относятся к сопротивлениям, находящимся на значительном расстоянии (до 20 - 40 диаметров) одно от другого. При близком расположении местных сопротивлений их необходимо рассматривать как сложное единое сопротивление. Расчет трубопроводов В зависимости от соотношения потерь напора по длине и местных потерь напора различают длинные и короткие трубопроводы. Если местные потери напора превышают 10 % потерь напора по длине, то такой трубопровод, как правило, имеющий сравнительно небольшую длину, называют коротким. В случае длинных трубопроводов местными потерями напора пренебрегают. Кроме того, различают простые трубопроводы – не имеющие ответвлений и сложные - с ответвлениями. При гидравлическом расчете трубопроводов встречаются три задачи: 1. определение расхода Q при заданных длине l, диаметре d и потерях напора hf; 2. определение потерь напора hf при заданных длине l, диаметре d и расходе Q; 3. определение диаметра трубопровода при заданных длине l, расходе Q и потерях напора hf.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
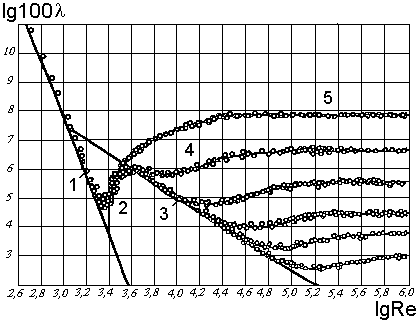
 2320
2320  Потери напора пропорциональны скорости в первой степени.
II.Переходная область
2320
Потери напора пропорциональны скорости в первой степени.
II.Переходная область
2320 
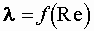
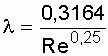 .
.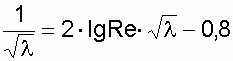 .
. ламинарная пленка становится тоньше, неровности начинают “обнажаться”, труба становится гидравлически шероховатой. В этом случае
ламинарная пленка становится тоньше, неровности начинают “обнажаться”, труба становится гидравлически шероховатой. В этом случае 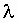 является функцией не только числа
является функцией не только числа  .
. ;
;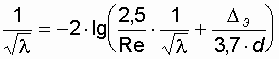 .
.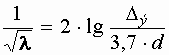 .
.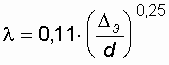 .
.
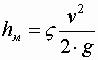 ,
,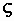 - коэффициент местного сопротивления.
- коэффициент местного сопротивления.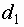 переходит в трубу с большим диаметром
переходит в трубу с большим диаметром 
 . Струя, выходящая из первой трубы, на некоторой длине расширяется и в сечении 2-2 заполняет все сечение второй трубы (рис. 2.1).
. Струя, выходящая из первой трубы, на некоторой длине расширяется и в сечении 2-2 заполняет все сечение второй трубы (рис. 2.1).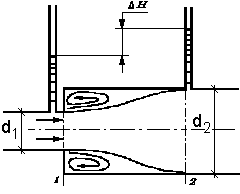 Рис. 2.1. Внезапное расширение
Рис. 2.1. Внезапное расширение

 , а в сечении 2-2 - через
, а в сечении 2-2 - через 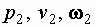 (рис.2.1). Будем считать, что распределение скоростей в сечениях 1-1 и 2-2 равномерное, то есть
(рис.2.1). Будем считать, что распределение скоростей в сечениях 1-1 и 2-2 равномерное, то есть 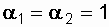 , касательное напряжение на стенке трубы между сечениями равно нулю, давление
, касательное напряжение на стенке трубы между сечениями равно нулю, давление 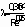 в сечении 1-1 действует по всей площади
в сечении 1-1 действует по всей площади 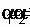

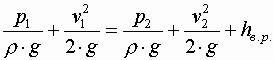 .
.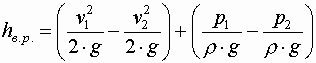 .
.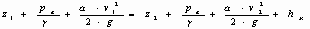 .
.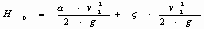

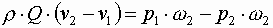
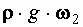 и учитывая, что
и учитывая, что 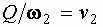
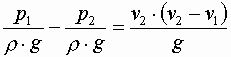 .
.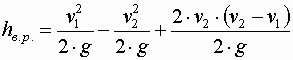 .
.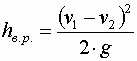 .
.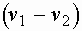 называют потерянной скоростью.
называют потерянной скоростью.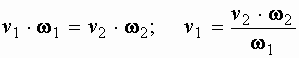 .
.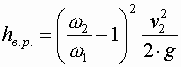 .
.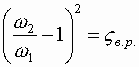 ,
, - коэффициент гидравлического сопротивления при внезапном расширении потока.
- коэффициент гидравлического сопротивления при внезапном расширении потока. .
.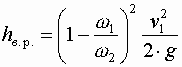 .
. ,
,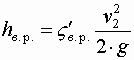 .
.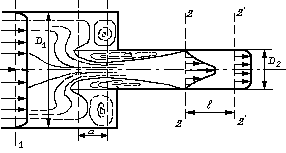 Рис. 2.2. Внезапное сжатие потока
Рис. 2.2. Внезапное сжатие потока
 в трубу меньшего диаметра
в трубу меньшего диаметра 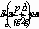 , а затем наступает его расширение до
, а затем наступает его расширение до 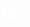 . Многочисленные исследования показали, потери напора на участке сжатия (от
. Многочисленные исследования показали, потери напора на участке сжатия (от  до
до 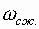 )
)
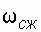 до
до 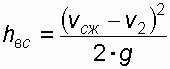 .
. .
.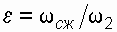 ,
,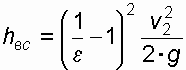 .
.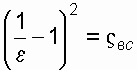
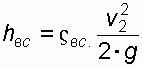 ,
, - коэффициент местного сопротивления при внезапном сжатии потока.
- коэффициент местного сопротивления при внезапном сжатии потока. зависит от степени сжатия потока
зависит от степени сжатия потока  .
.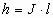 ;
;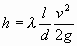 ;
; ;
; ;
; ;
; 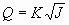 ;
; 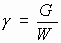 ;
;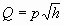 .
.