
|
|
Два режима движения жидкостиТечение реальной жидкости характеризуется различными режимами ее движения, которые могут переходить один в другой при определенных условиях. Экспериментальные исследования гидравлических сопротивлений показывают, что потери напора (потери энергии) зависят от существующего в потоке режима движения. Существование двух принципиально разных режимов движения жидкости было отмечено Г. Хагеном в 1839 и 1854 гг. При изучении течения всевозможных капельных жидкостей с различными физическими свойствами Рейнольдс установил, что движение бывает ламинарным и турбулентным. “Ламинарный” происходит от латинского слова lamina - слой. Ламинарным называется такой режим, когда поток жидкости движется отдельными струйками или слоями и траектории отдельных частиц между собой не пересекаются. В практике ламинарный режим имеет место при движении жидкостей с большой вязкостью (нефти, смазочных масел), при движении воды через тонкие трубки, в трубопроводах при малых скоростях потока. “Турбулентный” происходит от латинского слова turbulentus - беспорядочный. Турбулентным называется такой режим, когда струйчатость потока нарушается, все струйки перемешиваются, и траектории движущихся частиц приобретают сложную форму, пересекаясь между собой. В практике чаще всего имеет место турбулентный режим движения жидкости. В 1883 г. Рейнольдс в результате экспериментальных исследований установил, что критерием режима движения жидкости является безразмерная величина, представляющая собой отношение произведения средней скорости потока v и характерного для рассматриваемого случая линейного размера L к кинематической вязкости жидкости n :
При напорном движении жидкости в круглых трубах за характерный линейный размер L обычно принимают внутренний диаметр трубы D и тогда
а в остальных случаях - гидравлический радиус R
Физический смысл числа Рейнольдса состоит в том, что оно выражает отношение сил инерции к силам вязкости:
При преобладании сил вязкости - режим ламинарный, при преобладании сил инерции - режим турбулентный. Многочисленные экспериментальные исследования гидравлических сопротивлений показывают, что между ними и скоростью движения жидкости имеется зависимость hl = f(v). Если опытные данные нанести на график в логарифмических координатах, то можно выявить три области: ламинарную (линия AB), турбулентную (линия CD) и неустойчивую, расположенную между точками B и C.
Значение числа Рейнольдса, соответствующее нижней критической точке В, называется нижним критическим числом Рейнольдса и равно
Число Рейнольдса, соответствующее верхней критической точке С, называется верхним критическим числом и равно
Для напорного движения в цилиндрических трубах нижнее критическое число равно 956, то есть ламинарный режим устойчив, если Re В результате изучения движения жидкости, проведенного многими исследователями, в круглых гидравлически “гладких” трубах на участках, достаточно удаленных от входа, при отсутствии различных источников возмущения установлено критическое число Рейнольдса Reкр = 2000 - 2320. При Re < Reкр имеет место ламинарный режим движения. При Re > Reкр - турбулентный. Потери напора по длине связаны со скоростью зависимостью, которая выражается уравнением
где hl - потери напора по длине; a - коэффициент пропорциональности; v - средняя скорость потока; m - показатель степени. Прологарифмировав данное уравнение, можно получить линейную зависимость
откуда
При постепенном увеличении скорости движения воды в трубе картина движения в начале не меняется, но затем при определенной скорости движения наступает быстрое ее изменение. Струйка красителя по выходе из трубки начинает колебаться, в ней появляются разрывы. Затем она размывается и перемешивается с потоком воды, причем становятся заметными вихреобразования и вращательное движение жидкости. Движение становится турбулентным. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
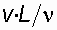 . Этот критерий называется числом Рейнольдса и обозначается Re. Таким образом, число Рейнольдса имеет вид
. Этот критерий называется числом Рейнольдса и обозначается Re. Таким образом, число Рейнольдса имеет вид .
. ,
, .
.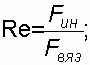
 ;
; ;
; (5.4)
(5.4)
 . (5.5)
. (5.5) (5.6)
(5.6) 956.
956. , (5.7)
, (5.7) , (5.8)
, (5.8) . (5.9)
. (5.9)
