|
|
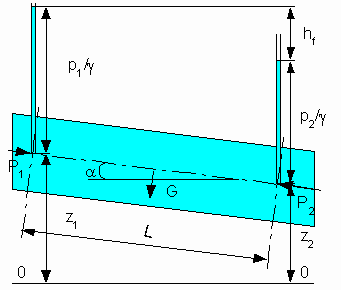
Основное уравнение установившегося равномерного движения
сила трения возникающая на поверхности соприкосновения жидкости со стенками T=t L c , направленная противоположно движению. Так как движение равномерное (без ускорения) силы инерции не возникают. Спроецируем силы на ось направления движения.
Разделим на g w
Напряжение силы трения отнесенное к единице веса равно произведению гидравлического радиуса на гидравлический уклон.
Ламинарный режим Исследуем ламинарный режим движения жидкости теоретически.
r = 0 t = 0 r = r0 Из последнего выражения виден линейный закон изменения касательного напряжения по сечению.
С другой стороны
Следовательно
Постоянная интегрирования
Окончательно, подставив значение
где Уравнение, известное как формула Стокса, представляет уравнение параболы, имеющей максимум при
Зная закон распределения скорости по живому сечению трубы, получим зависимость для определения расхода
Зависимость, определяющая расход носит название формулы Пуазейля. Так как
то есть средняя скорость в трубе при ламинарном режиме равна половине максимальной скорости, наблюдаемой на оси. Преобразуем зависимость
откуда
где Зависимость, определяющая величину потерь напора при ламинарном режиме движения, показывает, что потери напора при ламинарном режиме пропорциональны первой степени средней скорости, зависят от рода жидкости, обратно пропорциональны площади сечения трубы и не зависят от шероховатости стенок трубы. Преобразуем зависимость, умножив числитель и знаменатель на
ПОНЯТИЕ О ГИДРАВЛИЧЕСКИ ГЛАДКИХ И ШЕРОХОВАТЫХ ПОВЕРХНОСТЯХ
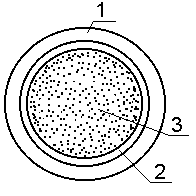
Поверхность стенок всегда обладает неровностями. Эти неровности имеют различную величину, форму и периодичность, которые зависят от рода материала и способа его изготовления. Величина неровностей характеризуется абсолютной шероховатостью, представляющая собой среднюю линейную величину неровностей. Если величина выступов меньше толщины ламинарного подслоя, то такая поверхность называется гидравлически гладкой. В этом случае потери энергии на трение не будут зависеть от шероховатости поверхности. Если неровности выступают сквозь ламинарную пленку, то поверхность называется гидравлически шероховатой. Толщина ламинарного слоя зависит от числа Рейнольдса (с увеличением Re толщина уменьшается), следовательно, одна и та же поверхность в различных гидравлических режимах может быть гидравлически гладкой или шероховатой. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
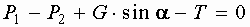
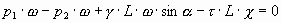
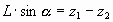
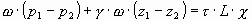
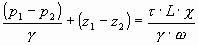
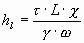
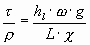
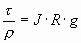
 - динамическая скорость. Эта величина не имеет физического смысла, но имеет размерность скорости.
- динамическая скорость. Эта величина не имеет физического смысла, но имеет размерность скорости.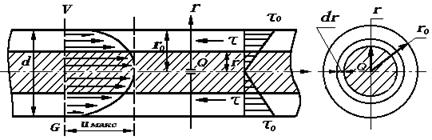
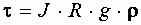
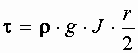


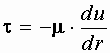
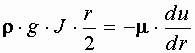
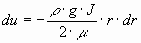
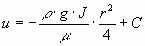
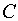 определяется из условия равенства нулю скорости
определяется из условия равенства нулю скорости  у стенок трубы при
у стенок трубы при 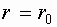
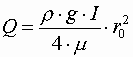 .
.
 - коэффициент кинематической вязкости.
- коэффициент кинематической вязкости.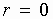 , то есть по оси трубы
, то есть по оси трубы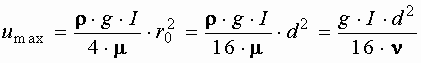
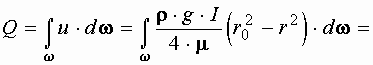
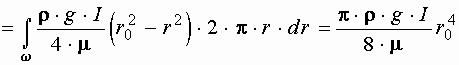 .
.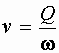 , получаем
, получаем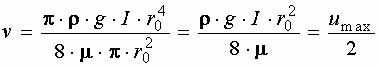 ,
,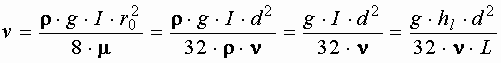 ,
,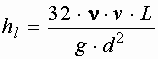 ,
,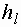 - потери напора по длине.
- потери напора по длине.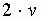 и перегруппировав сомножители
и перегруппировав сомножители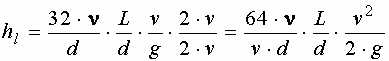 .
.