
|
|
ОТНОСИТЕЛЬНЫЙ ПОКОЙ ЖИДКОСТИЛ. Эйлером в 1755 г. были получены дифференциальные уравнения равновесия жидкости:
где После незначительных преобразований данную систему уравнений можно представить в виде уравнения
Полученное уравнение (2) выражает приращение давления dP при изменении координат на dx, dy, dz в общем случае равновесия жидкости. Поверхность жидкости, во всех точках которой давление одинаково, называется поверхностью равного давления или поверхностью уровня. Для поверхности равного давления dP = 0, а с учетом, что r = const уравнение (2) примет вид
Уравнение (3) устанавливает связь между координатами свободной поверхности и действующими на жидкость массовыми силами, единичные проекции которых равны X, Y, Z. Поверхности уровня жидкостей, соприкасающиеся с газообразной средой (чаще атмосферной), называются свободными поверхностями. Комбинация массовых сил, действующих на жидкость может быть разной. Если жидкость покоится в сосуде, неподвижном относительно Земли (то есть вращением жидкости вместе с Землей можно пренебречь), то такое равновесное состояние жидкости можно назвать “абсолютным” покоем. При “абсолютном” покое жидкость находится под действием лишь одной массовой силы - силы тяжести. Если сосуд с жидкостью находится в неравномерном или непрямолинейном движении, то на жидкость кроме сил тяжести действуют силы инерции. Силы инерции могут быть постоянны по времени, поэтому равновесие жидкости в этом случае называется “относительным” покоем. При “относительном” покое свободная поверхность жидкости или поверхность уровня принимает другие формы по сравнению с формой при “абсолютном” покое. Рассмотрим формы поверхности равного давления и свободные поверхности жидкости при разных комбинациях массовых сил. Случай 1. Жидкость находится по действием только силы тяжести . При условии, что ось z направлена вертикально вверх, проекции силы тяжести на ось (x) Х = 0; на ось (y) Y = 0; на ось (z) Z = - g. (Вообще-то Z = -mg, но данных уравнениях идет расчет на единицу массы, т.е. m = 1) Дифференциальное уравнение (3) в этом случае примет вид
или после интегрирования: z = const. (5) Уравнение (5) является уравнением горизонтальной плоскости, форму которой имеют все поверхности равного давления и свободная поверхность, когда на жидкость действует только сила тяжести (рис. 1).
Рис.1 Абсолютный покой жидкости Случай 2. Жидкость находится в сосуде, который движется прямолинейно равномерно - ускорено. На жидкость, в этом случае действуют не только силы тяжести , но и силы инерции, которые характеризуются ускорением а и направлены противоположно движению. Проекции этих единичных сил на соответствующие координатные оси равны Дифференциальное уравнение (3) примет вид
или после интегрирования
Уравнение (7) является уравнением наклонной горизонтальной плоскости (рис. 2), угол наклона которой к горизонту b определяется отношением
Случай 3. Жидкость находится в сосуде, который равномерно вращается вокруг вертикальной оси с постоянной угловой скоростью w (рис.3) В этом случае на жидкость действуют помимо сил тяжести и центробежные силы. Проекции ускорения этих сил на координатные оси соответственно равны X = w 2 x, Y = w 2 y, Z = - g. Дифференциальное уравнение (3) примет вид
или после интегрирования
Учитывая, что окончательно получим Уравнение (13) является уравнением параболоида вращения, который в сечении вертикальными плоскостями дает параболы, а в горизонтальной плоскости окружности. Положение любой точки свободной поверхности, например точки В (рис. 4) определяется координатой
где rB - радиус точки В. Самой высокой точкой свободной поверхности является точка на стенке резервуара D (рис. 4). Ее координата соответственно будет равна
где R - радиус резервуара. Одновременно координата ZD является высотой параболоида вращения. По отношению к дну точка D, как самая высокая точка свободной поверхности, находится на расстоянии
Самой низкой точкой параболоида вращения является точка О на оси цилиндра (начало координат). Точка О соответствует максимальному понижению свободной поверхности по оси резервуара относительно статического уровня Н. Ее расстояние от дна резервуара h0 равно
Следовательно, при вращении жидкость поднимается у стенки и опускается по оси резервуара по отношению к статическому уровню на одну и ту же величину Значение избыточного давления внутри жидкости при вращении согласно уравнению (13) определится
где ri - радиус рассматриваемой i - точки; zi - расстояние от начала координат до рассматриваемой i - точки (рис.4). Самое малое избыточное давление на дно будет по оси вращения в центре резервуара
Самое большое избыточное давление на дно возникает у стенки
Эпюра избыточного давления на дно и стенки резервуара имеет вид (рис.5).
6. КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Как изменяется давление вдоль оси Х при “абсолютном” покое? 2. Как изменяется давление вдоль оси Х, если сосуд с жидкостью движется прямолинейно с постоянным ускорением совпадающим с направлением оси Х? 3. Как изменяется давление вдоль оси Х, если сосуд с жидкостью движется прямолинейно с постоянным ускорением направленным противоположно направлению оси Х? 4. Как изменяется давление вдоль оси Х, если сосуд с жидкостью движется в направлении оси Х равномерно и прямолинейно? 5. Что называется свободной поверхностью и поверхностями уровня? 6. Как изменяется давление вдоль радиуса сосуда с жидкостью, вращающегося с постоянной частотой вдоль вертикальной оси, проходящей через его середину? 7. Что представляет собой свободная поверхность, если сосуд с жидкостью движется равномерно и прямолинейно? 8. Что представляет собой свободная поверхность, если сосуд с жидкостью движется прямолинейно с постоянным ускорением? 9. Что представляет собой свободная поверхность, если сосуд с жидкостью вращается вокруг вертикальной оси, проходящей через центр сосуда? 10. Что представляет собой свободная поверхность, если сосуд с жидкостью равномерно движется по окружности? 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 (1)
(1) - градиенты давления в направлении соответствующих координатных осей; X, Y, Z -проекции ускорений единичных массовых сил на соответствующие оси; r - плотность. В обычных условиях действует одна массовая сила - сила тяжести.
- градиенты давления в направлении соответствующих координатных осей; X, Y, Z -проекции ускорений единичных массовых сил на соответствующие оси; r - плотность. В обычных условиях действует одна массовая сила - сила тяжести.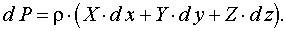 (2)
(2) (3)
(3)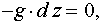 (4)
(4)
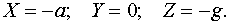
 (6)
(6) (7)
(7) (8)
(8)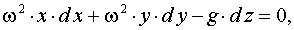 (9)
(9) (10)
(10) 11)
11)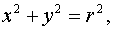 (12)
(12) (13)
(13) (14)
(14) (15)
(15) (16)
(16) (17)
(17)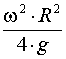 . При большой угловой скорости вращения возможно оголение дна, а при недостаточной высоте стенки переливание жидкости через нее.
. При большой угловой скорости вращения возможно оголение дна, а при недостаточной высоте стенки переливание жидкости через нее. (14)
(14) (15)
(15) (16)
(16)