
|
|
Кристаллические и аморфные тела
По своим физическим свойствам и молекулярной структуре твердые тела разделяются на два класса - аморфные и кристаллические тела. Характерной особенностью аморфных тел является их изотропность, т.е. независимость всех физических свойств (механических, оптических и т.д.) от направления. Примерами аморфных тел могут служить стекло, различные затвердевшие смолы (янтарь), пластики и т.д. Если аморфное тело нагревать, то оно постепенно размягчается, и переход в жидкое состояние занимает значительный интервал температур. В кристаллических телах частицы располагаются в строгом порядке, образуя пространственные периодически повторяющиеся структуры во всем объеме тела. Для наглядного представления таких структур используются пространственные кристаллические решетки, в узлах которых располагаются центры атомов или молекул данного вещества. Чаще всего кристаллическая решетка строится из ионов (положительно и отрицательно заряженных) атомов, которые входят в состав молекулы данного вещества.
Кристаллические тела могут быть монокристаллами и поликристаллами. Поликристаллические тела состоят из многих сросшихся между собой хаотически ориентированных маленьких кристалликов, которые называются кристаллитами. Большие монокристаллы редко встречаются в природе и технике. Чаще всего кристаллические твердые тела, в том числе и те, которые получаются искусственно, являются поликристаллами. В отличие от монокристаллов поликристаллические тела изотропны, т.е. их свойства одинаковы во всех направлениях. Поликристаллическое строение твердого тела можно обнаружить с помощью микроскопа.
В простой кубической решетке частицы располагаются в вершинах куба. В гранецентрированной решетке частицы располагаются не только в вершинах куба, но и в центрах каждой его грани. Кристаллические структуры металлов имеют важную особенность. Деформация. В твердых телах - аморфных и кристаллических - частицы (молекулы, атомы, ионы) совершат тепловые колебания около положений равновесия, в которых энергия их взаимодействия минимальна. Силы взаимодействия между частицами обуславливают механические свойства твердых тел. Деформация твердого тела является результатом изменения под действием внешних сил взаимного расположения частиц, из которых состоит тело, и расстояний между ними. Простейшим видом деформации является деформация растяжения или сжатия. Ее можно характеризовать абсолютным удлинением Отношение абсолютного удлинения При растяжении
Зависимость между Максимальное значение Коэффициент E в этом соотношении называется модулем Юнга. Максимальное напряжение называется пределом упругости . Если Материалы, у которых диаграмма растяжения имеет вид, показанный на рисунке, называются пластичными. Материалы, у которых разрушение происходит при деформациях, лишь незначительно превышающих область упругих деформаций, называются хрупкими (стекло, фарфор, чугун).
Контрольные вопросы и задания. Вопрос 1. Чем отличается аморфное тело от кристаллического? Вопрос 2. Приведите примеры аморфных тел. Вопрос 3. Перечислите основные виды деформации твердых тел. Вопрос 4. Чем отличаются упругие деформации от пластических? Вопрос 5. Что называют пределом прочности? Вопрос 6. Какие материалы называют хрупкими? Вопрос 7. Какие силы межмолекулярного взаимодействия являются преобладающими при деформации сжатия?
Пример. К медной проволоке длиной l=1 м и радиусом r=1 мм подвесили груз массой m=20 кг. Предполагая деформацию упругой, определите работу растяжения проволоки. Модуль Юнга меди равен E=1.1·1011 Па. Решение.
где
Роль коэффициента жесткости проволоки играет величина k=ES/l. Окончательно получим:
Задача 1. К закрепленной одним концом проволоке сечением 0.2 см2 подвешен груз массой 1 кг. Рассчитайте механическое напряжение в проволоке Задача 2. Имеются два стержня с длинами l1 = l и l2 = 2l одинакового сечения и изготовленные из одинакового материала. Сравните удлинения Задача 3. Имеются два стержня одинаковой длины и сечения, изготовленные из одинакового материала. Сравните удлинения Задача 4. Предел прочности на сжатие кирпича Задача 5. Масса кабины лифта вместе с пассажирами m=500 кг. Кабина подвешена на тросе, изготовленном из стали с пределом прочности на растяжение
Задача 6. Из скольких проволок должен состоять стальной канат, рассчитанный на подъем груза массой m=3·103 кг, если запас прочности должен быть равен k=4. Диаметр проволоки d=1 мм. Предел прочности стали

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
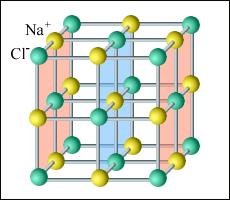 Например, решетка поваренной соли содержит ионы Na+ и Cl-, не объединенные попарно в молекулы NaCl. Такие кристаллы называются ионными.
Например, решетка поваренной соли содержит ионы Na+ и Cl-, не объединенные попарно в молекулы NaCl. Такие кристаллы называются ионными.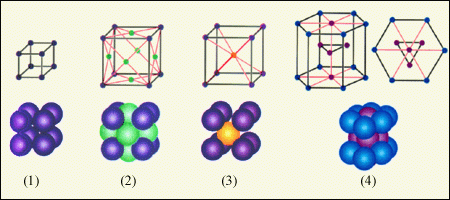 На рисунке приведены примеры простых кристаллических решеток. В изображении кристаллических решеток указывается только положение центров частиц.
На рисунке приведены примеры простых кристаллических решеток. В изображении кристаллических решеток указывается только положение центров частиц. Существует несколько видов деформаций твердых тел. Некоторые из них представлены на рисунке
Существует несколько видов деформаций твердых тел. Некоторые из них представлены на рисунке , возникающим под действием внешней силы
, возникающим под действием внешней силы  . Связь между
. Связь между 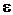 :
: 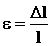
 , при сжатии
, при сжатии  .
. Если принять направление внешней силы, стремящейся удлинить образец, за положительное, то F>0 при деформации растяжения и F<0 - при сжатии. Отношение модуля внешней силы F к площади S сечения тела называется механическим напряжением
Если принять направление внешней силы, стремящейся удлинить образец, за положительное, то F>0 при деформации растяжения и F<0 - при сжатии. Отношение модуля внешней силы F к площади S сечения тела называется механическим напряжением  :
:  За единицу механического напряжения в СИ принят паскаль (Па). Механическое напряжение измеряется в единицах давления.
За единицу механического напряжения в СИ принят паскаль (Па). Механическое напряжение измеряется в единицах давления. , при котором сохраняется линейная связь между
, при котором сохраняется линейная связь между 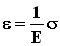
 , образец после снятия напряжения уже не восстанавливает свои первоначальные размеры и у тела сохраняется остаточная деформация
, образец после снятия напряжения уже не восстанавливает свои первоначальные размеры и у тела сохраняется остаточная деформация  . Такие деформации называются пластическими (участки bc, cd и de). На участке bc деформация происходит почти без увеличения напряжения. Это явление называется текучестью материала. В точке d достигается наибольшее напряжение
. Такие деформации называются пластическими (участки bc, cd и de). На участке bc деформация происходит почти без увеличения напряжения. Это явление называется текучестью материала. В точке d достигается наибольшее напряжение  , которое способен выдержать материал без разрушения (предел прочности). В точке e происходит разрушение материала.
, которое способен выдержать материал без разрушения (предел прочности). В точке e происходит разрушение материала. Вопрос 8. На рисунке представлена диаграмма растяжения материала. Какая точка на диаграмме соответствует пределу прочности данного материала?
Вопрос 8. На рисунке представлена диаграмма растяжения материала. Какая точка на диаграмме соответствует пределу прочности данного материала?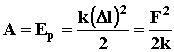 ,
, - приложенная сила,
- приложенная сила,  - удлинение пружины, k - жесткость, которую можно найти из закона Гука
- удлинение пружины, k - жесткость, которую можно найти из закона Гука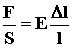 или
или  .
. Дж.
Дж. и
и 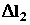 стержней, если приложенные к ним напряжения одинаковы.
стержней, если приложенные к ним напряжения одинаковы. Н/м2, для бетона
Н/м2, для бетона  Н/м2. Плотность кирпича
Н/м2. Плотность кирпича 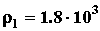 кг/м3, плотность бетона
кг/м3, плотность бетона  кг/м3. Подсчитайте, какой предельной высоты здания можно построить из кирпича и из бетона при коэффициенте запаса прочности k=6.
кг/м3. Подсчитайте, какой предельной высоты здания можно построить из кирпича и из бетона при коэффициенте запаса прочности k=6. Н/м2. Лифт движется вверх с ускорением a=0.5 м/с2. Каким должно быть сечение S троса, если коэффициент запаса прочности k=15?
Н/м2. Лифт движется вверх с ускорением a=0.5 м/с2. Каким должно быть сечение S троса, если коэффициент запаса прочности k=15? Н/м2.
Н/м2.