Собственные векторы и собственные значения линейного оператора.
Пусть 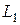 – одномерное инвариантное подпространство, порождаемое вектором – одномерное инвариантное подпространство, порождаемое вектором  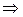 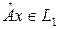 , т.е. , т.е.  . .
Определение 12. Вектор 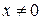 , удовлетворяющий условию , удовлетворяющий условию 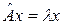 , называется собственным вектором, а соответствующее число , называется собственным вектором, а соответствующее число 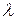 – собственным числом (характеристическим числом) линейного оператора – собственным числом (характеристическим числом) линейного оператора 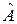 . .
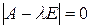 - характеристическое уравнение матрицы А. Многочлен, стоящий в левой части характеристического уравнения, называется характеристическим многочленом матрицы - характеристическое уравнение матрицы А. Многочлен, стоящий в левой части характеристического уравнения, называется характеристическим многочленом матрицы  . .
Свойства собственных векторов и собственных значений.
1°. Все собственные векторы, принадлежащие одному и тому же собственному значению, вместе с нулевым вектором образуют линейное подпространство. Действительно, они получены как решения СЛОУ 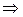 образуют линейное подпространство. образуют линейное подпространство.
2°. Теорема 4. Если собственные векторы 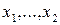 , принадлежат попарно различным собственным значениям, то они линейно независимы. , принадлежат попарно различным собственным значениям, то они линейно независимы.
3°. Если  и и  – матрицы линейного преобразования – матрицы линейного преобразования 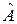 в различных базисах, то характеристические многочлены этих матриц совпадают. в различных базисах, то характеристические многочлены этих матриц совпадают.
4°. У характеристического многочлена могут быть простые корни, т.е. кратности 1, а могут быть кратные корни.
Теорема 4. Пусть  – корень характеристического многочлена кратности – корень характеристического многочлена кратности 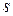 . Тогда, ему соответствует не более . Тогда, ему соответствует не более 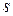 линейно независимых собственных векторов. линейно независимых собственных векторов.
5°. Линейное преобразование имеет собственное значение, равное нулю 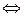 оно не является взаимно однозначным. оно не является взаимно однозначным.
Определение 1. Линейное преобразование  евклидова пространства называется сопряженным данному преобразованию евклидова пространства называется сопряженным данному преобразованию 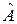 , если , если 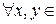 E E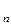 : :
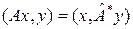 . .
Свойства сопряженных операторов.
1°. 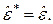
2°. 
3°. 
4°. 
5°. 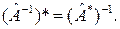
Определение 2. Линейное преобразование 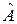 евклидова пространства называется самосопряженным или симметрическим, если евклидова пространства называется самосопряженным или симметрическим, если 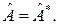
Определение 1. Линейное преобразование 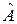 в евклидовом пространстве E в евклидовом пространстве E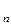 называется ортогональным, если оно сохраняет скалярное произведение, т.е. называется ортогональным, если оно сохраняет скалярное произведение, т.е. 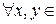 E E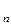 => => 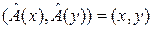 . .
Определение 2. Если  , то преобразование называется собственным, если , то преобразование называется собственным, если 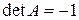 , то несобственным. , то несобственным.
Жорданова форма
Определение 1.Вектор 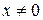 называется собственным вектором преобразования называется собственным вектором преобразования 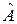 , отвечающим собственному значению , отвечающим собственному значению  , если , если
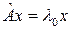 , т.е. , т.е. 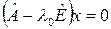 . .
Определение 2.Вектор  называется присоединенным вектором первого порядка преобразования называется присоединенным вектором первого порядка преобразования 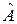 , отвечающим собственному значению , отвечающим собственному значению  , если вектор , если вектор 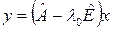 является собственным вектором преобразования является собственным вектором преобразования 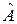 . .
Определение 3.Вектор  называется присоединенным вектором называется присоединенным вектором  –го порядка, если вектор –го порядка, если вектор 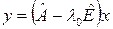 является присоединенным вектором является присоединенным вектором  – го порядка. – го порядка.
По индукции можно показать, что если  – присоединенный вектор – присоединенный вектор  – го порядка, то – го порядка, то  , , 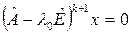 . .
Определение 4. Векторы из пространства  называются относительно линейно независимыми над пространством называются относительно линейно независимыми над пространством  , если их линейная комбинация, отличная от нуля, не принадлежит , если их линейная комбинация, отличная от нуля, не принадлежит  . .
Определение 5. Базисом пространства  относительно подпространства относительно подпространства  называется такая система называется такая система 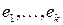 линейно независимых векторов из линейно независимых векторов из  , которая после пополнения каким-нибудь базисом из , которая после пополнения каким-нибудь базисом из  образует базис во всем пространстве. образует базис во всем пространстве.
 = =  - жорд. клетка, отвечающая собств. значению - жорд. клетка, отвечающая собств. значению 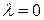 . .
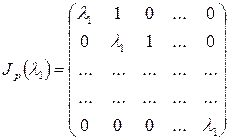 - жордановы клетки матрицы преобразования - жордановы клетки матрицы преобразования 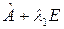 . .
Линии второго порядка
Определение 1. Эллипсом называется множество точек плоскости, сумма расстояний от которых до двух данных точек  и и 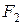 этой плоскости, называемых фокусами эллипса, есть величина постоянная, большая, чем расстояние между фокусами. этой плоскости, называемых фокусами эллипса, есть величина постоянная, большая, чем расстояние между фокусами.
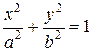 - каноническое уравнение эллипса. Числа - каноническое уравнение эллипса. Числа  и и 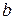 называются соответственно большой и малой полуосями эллипса. называются соответственно большой и малой полуосями эллипса.
Определение 2.Число 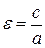 называется эксцентриситетом эллипса. называется эксцентриситетом эллипса.
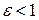 . Эксцентриситет характеризует форму эллипса: если . Эксцентриситет характеризует форму эллипса: если  , то , то 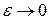 , а эллипс становится похожим на окружность. При увеличении , а эллипс становится похожим на окружность. При увеличении  эллипс становится более вытянутым. эллипс становится более вытянутым.
Определение 3. Гиперболой называется множество точек плоскости, модуль разности расстояний от которых до двух данных точек 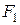 и и 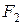 этой плоскости, называемых фокусами, есть величина постоянная, не равная нулю и меньшая, чем расстояние между фокусами. этой плоскости, называемых фокусами, есть величина постоянная, не равная нулю и меньшая, чем расстояние между фокусами.
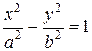 - каноническое уравнение гиперболы. - каноническое уравнение гиперболы.
Определение 4.Эксцентриситетом гиперболы называется число
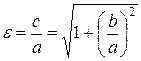 . .
 . Эксцентриситет характеризует форму гиперболы: чем меньше . Эксцентриситет характеризует форму гиперболы: чем меньше  , тем больше вытягивается основной прямоугольник (так как , тем больше вытягивается основной прямоугольник (так как  ), а вслед за ним и гипербола вдоль оси ), а вслед за ним и гипербола вдоль оси 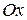 . .
Определение 5. Параболой называется множество точек плоскости, каждая из которых равноудалена от точки 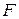 и прямой и прямой 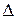 . Точка . Точка 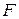 называется фокусом параболы, прямая называется фокусом параболы, прямая 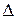 – директрисой параболы. – директрисой параболы.
 - каноническое уравнение параболы, p – фокальный параметр. - каноническое уравнение параболы, p – фокальный параметр.
Фокальный параметр  равен длине перпендикуляра к оси параболы, восстановленного из фокуса до точки пересечения с параболой. Он характеризует форму параболы. равен длине перпендикуляра к оси параболы, восстановленного из фокуса до точки пересечения с параболой. Он характеризует форму параболы.
Определение 6. Две прямые, перпендикулярные к большой оси эллипса и расположенные симметрично относительно центра на расстоянии  от него, называются директрисами эллипса. от него, называются директрисами эллипса.
Определение 7. Две прямые, перпендикулярные к той оси гиперболы, которая её пересекает, и расположенные симметрично относительно центра на расстоянии  от него, называются директрисами гиперболы. от него, называются директрисами гиперболы.
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|


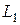 – одномерное инвариантное подпространство, порождаемое вектором
– одномерное инвариантное подпространство, порождаемое вектором 
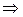
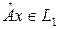 , т.е.
, т.е.  .
.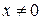 , удовлетворяющий условию
, удовлетворяющий условию 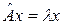 , называется собственным вектором, а соответствующее число
, называется собственным вектором, а соответствующее число 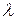 – собственным числом (характеристическим числом) линейного оператора
– собственным числом (характеристическим числом) линейного оператора 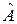 .
.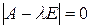 - характеристическое уравнение матрицы А. Многочлен, стоящий в левой части характеристического уравнения, называется характеристическим многочленом матрицы
- характеристическое уравнение матрицы А. Многочлен, стоящий в левой части характеристического уравнения, называется характеристическим многочленом матрицы  .
.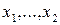 , принадлежат попарно различным собственным значениям, то они линейно независимы.
, принадлежат попарно различным собственным значениям, то они линейно независимы. – матрицы линейного преобразования
– матрицы линейного преобразования  – корень характеристического многочлена кратности
– корень характеристического многочлена кратности 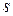 . Тогда, ему соответствует не более
. Тогда, ему соответствует не более 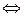 оно не является взаимно однозначным.
оно не является взаимно однозначным. евклидова пространства называется сопряженным данному преобразованию
евклидова пространства называется сопряженным данному преобразованию 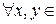 E
E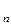 :
: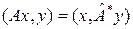 .
.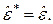



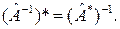
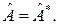
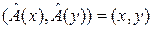 .
. , то преобразование называется собственным, если
, то преобразование называется собственным, если 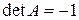 , то несобственным.
, то несобственным.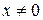 называется собственным вектором преобразования
называется собственным вектором преобразования 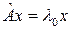 , т.е.
, т.е. 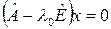 .
.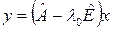 является собственным вектором преобразования
является собственным вектором преобразования  –го порядка, если вектор
–го порядка, если вектор 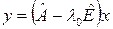 является присоединенным вектором
является присоединенным вектором  – го порядка.
– го порядка. ,
, 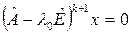 .
. называются относительно линейно независимыми над пространством
называются относительно линейно независимыми над пространством  , если их линейная комбинация, отличная от нуля, не принадлежит
, если их линейная комбинация, отличная от нуля, не принадлежит 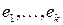 линейно независимых векторов из
линейно независимых векторов из  =
=  - жорд. клетка, отвечающая собств. значению
- жорд. клетка, отвечающая собств. значению 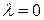 .
.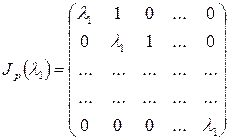 - жордановы клетки матрицы преобразования
- жордановы клетки матрицы преобразования 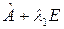 .
. и
и 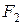 этой плоскости, называемых фокусами эллипса, есть величина постоянная, большая, чем расстояние между фокусами.
этой плоскости, называемых фокусами эллипса, есть величина постоянная, большая, чем расстояние между фокусами.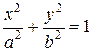 - каноническое уравнение эллипса. Числа
- каноническое уравнение эллипса. Числа  и
и 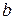 называются соответственно большой и малой полуосями эллипса.
называются соответственно большой и малой полуосями эллипса.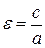 называется эксцентриситетом эллипса.
называется эксцентриситетом эллипса.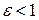 . Эксцентриситет характеризует форму эллипса: если
. Эксцентриситет характеризует форму эллипса: если  , то
, то 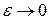 , а эллипс становится похожим на окружность. При увеличении
, а эллипс становится похожим на окружность. При увеличении  эллипс становится более вытянутым.
эллипс становится более вытянутым.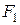 и
и 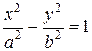 - каноническое уравнение гиперболы.
- каноническое уравнение гиперболы.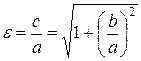 .
. . Эксцентриситет характеризует форму гиперболы: чем меньше
. Эксцентриситет характеризует форму гиперболы: чем меньше  ), а вслед за ним и гипербола вдоль оси
), а вслед за ним и гипербола вдоль оси 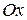 .
.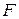 и прямой
и прямой 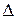 . Точка
. Точка  - каноническое уравнение параболы, p – фокальный параметр.
- каноническое уравнение параболы, p – фокальный параметр. равен длине перпендикуляра к оси параболы, восстановленного из фокуса до точки пересечения с параболой. Он характеризует форму параболы.
равен длине перпендикуляра к оси параболы, восстановленного из фокуса до точки пересечения с параболой. Он характеризует форму параболы. от него, называются директрисами эллипса.
от него, называются директрисами эллипса.