Свойства (сложения матриц).
1) Коммутативность: 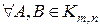 => =>  . .
2) Ассоциативность:  => =>  . .
3)  , где , где  - нулевая матрица. - нулевая матрица.
4)  . Матрица . Матрица  называется противоположной к называется противоположной к  и обозначается и обозначается  . .
Свойства (умножения матрицы на элемент кольца).
 выполняется выполняется
1)  . .
2)  . .
3)  . .
4)  . .
Свойства (умножения матриц).
1) Ассоциативность:  => =>  . .
2) Дистрибутивность сложения относительно умножения, т.е.,
 , ,  . .
 , ,  . .
3)  , где , где  - единичная матрица. - единичная матрица.
4)  . .
5)  . .
6)  . .
Определение 6. Прямой суммой  квадратных матриц квадратных матриц  порядков порядков  соответственно называется квадратная матрица соответственно называется квадратная матрица  порядка порядка  : :  . .
Свойства (прямой суммы).
1)  . .
2)  . .
3)  . .
4)  . .
Определение 1. Определителем квадратной матрицы  порядка порядка  с элементами из с элементами из  называется элемент кольца называется элемент кольца  : :
  = =  = =  , ,
где сумма берется по всем перестановкам  множества из множества из  элементов, элементов,  – знак перестановки. – знак перестановки.
Таким образом, из элементов  составляются всевозможные произведения составляются всевозможные произведения  из из  сомножителей, содержащих по одному элементу из каждого столбца и каждой строки. Всего слагаемых в сумме равно числу перестановок, т.е. равно сомножителей, содержащих по одному элементу из каждого столбца и каждой строки. Всего слагаемых в сумме равно числу перестановок, т.е. равно  . .
Определение 2. Матрица  Î Î  называется транспонированной к матрице называется транспонированной к матрице  , если она получается следующим образом: , если она получается следующим образом:  –й столбец матрицы –й столбец матрицы  состоит из элементов состоит из элементов  –ой строки матрицы –ой строки матрицы  , расположенных в том же порядке. , расположенных в том же порядке.
Операция  называется транспонированием. называется транспонированием.
Свойства операции транспонирования матриц.
1. 
2. 
3. 
4.  справедливо справедливо 
5. 
6. 
Определение 4. Если квадратная  , то , то  называется симметричной, тогда называется симметричной, тогда  , если , если  т.е. т.е.  , то , то  – называется кососимметричной (антисимметричной). – называется кососимметричной (антисимметричной).
Свойство 1. Определитель транспонированной матрицы равен определителю исходной матрицы, т.е. 
Свойство 2. Если одна из строк определителя состоит из 0,то определитель равен нулю.
Свойство 3. Если матрица  получена из получена из  перестановкой каких–либо двух строк, то перестановкой каких–либо двух строк, то 
Свойство 4. Определитель, содержащий две одинаковые строки, равен нулю.
Свойство 5. Если  получена из получена из  умножением некоторой строки на умножением некоторой строки на  , то , то  . .
Свойство 6. Если  содержит две пропорциональные строки, то содержит две пропорциональные строки, то  . .
Свойство 7.Если все элементы  –ой строки матрицы –ой строки матрицы  представлены в виде двух слагаемых: представлены в виде двух слагаемых:  , то , то  , где , где  , ,  имеют все строки, кроме имеют все строки, кроме  –ой, как в –ой, как в  , а , а  –ая строка –ая строка  состоит из состоит из  , а , а  – из – из  , т.е. , т.е.

Свойство 8. Если одна из строк определителя есть линейная комбинация его других строк, то определитель равен нулю.
Свойство 9. Определитель не меняется, если к элементам одной из его строк прибавляются соответствующие элементы другой строки, умноженные на одно и то же число.
Определение 5.Минором порядка  матрицы матрицы  называется определитель матрицы порядка называется определитель матрицы порядка  , образованной элементами, находящимися на пересечении выбранных строк и столбцов. , образованной элементами, находящимися на пересечении выбранных строк и столбцов.
Определение 6. Если  – квадратная порядка – квадратная порядка  , то каждому минору , то каждому минору  порядка порядка  можно поставить в соответствие дополнительный минор можно поставить в соответствие дополнительный минор  порядка порядка  , элементы которого расположены на пересечении остальных строк и столбцов. , элементы которого расположены на пересечении остальных строк и столбцов.
Алгебраическими дополнениями минора  называется произведение дополнительного минора на называется произведение дополнительного минора на  
Теорема 1(о разложении определителя).
Если  и и  , то , то  равен сумме произведений элементов любой строки матрицы равен сумме произведений элементов любой строки матрицы  на их алгебраические дополнения, т.е. на их алгебраические дополнения, т.е. 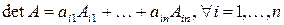 . .
Определение 1.Матрица  называется обратной для называется обратной для  , если , если  . .
Определение 2.Квадратная матрица  называется невырожденной (или неособой), если называется невырожденной (или неособой), если  и вырожденной (особой), если и вырожденной (особой), если  . .
Определение 3.Матрицей присоединенной к матрице  , называется матрица , называется матрица
 , ,
где  – алгебраическое дополнение элемента – алгебраическое дополнение элемента  матрицы матрицы  . .
Теорема 1: Для того, чтобы для матрица  существовала обратная, необходимо и достаточно, чтобы матрица существовала обратная, необходимо и достаточно, чтобы матрица  была невырожденной. была невырожденной.
Свойства обратных матриц:
Пусть  . Тогда . Тогда
1. 
2. 
3. 
4. 
5. 
Вычисление: 
Определение 1. Будем говорить, что строка  является линейной комбинацией строк является линейной комбинацией строк   , если для некоторых , если для некоторых  справедливо справедливо
 , ,  (1) (1)
Это равенство удобно записать в матричном виде:
 (1’) (1’)
Определение 2.Строки  назовем линейно зависимыми, если назовем линейно зависимыми, если   такие такие  одновременно не равные нулю, такие что одновременно не равные нулю, такие что

Строки, не являющиеся линейно зависимыми, являются линейно независимыми. Иными словами,  – линейно независимы, если равенство – линейно независимы, если равенство 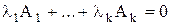 возможно лишь когда возможно лишь когда  . .
Теорема 1: Строки  – линейно зависимы – линейно зависимы 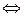 одна из этих строк является линейной комбинацией остальных. одна из этих строк является линейной комбинацией остальных.
Определение 3.Число  называется рангом матрицы называется рангом матрицы  , если , если
1)  минор порядка минор порядка  , отличный от нуля. , отличный от нуля.
2) Все миноры  –го порядка равны нулю. –го порядка равны нулю.
Т.о., рангом матрицы называется порядок наибольшего отличного от нуля минора.
Линейные пространства
Определение 1.Множество  вместе с заданными на нем операциями сложения векторов и умножения вектора на скаляр называется линейным (векторным) пространством над полем вместе с заданными на нем операциями сложения векторов и умножения вектора на скаляр называется линейным (векторным) пространством над полем  , если удовлетворяются следующие аксиомы: , если удовлетворяются следующие аксиомы:
1)  является абелевой группой; является абелевой группой;
2) Для любых  и и  выполняются равенства: выполняются равенства:
а) Умножение  на на  не изменяет не изменяет  , т.е. , т.е.  . .
б)   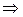  . .
в)   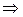 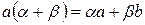 . .
г)   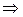  . .
Свойствалинейного пространства.
1)  => =>  . .
2)  => =>  . .
3)  => =>  . .
4)  => =>  . .
5)  . .
6)  . .
7)  . .
Определение 2.Линейной комбинацией векторов  с коэффициентами с коэффициентами  называется выражение вида: называется выражение вида:  . .
Определение 3.Вектора  называются линейно независимыми, если называются линейно независимыми, если  , из которых хотя бы одно отлично от нуля, т.е. линейная комбинация , из которых хотя бы одно отлично от нуля, т.е. линейная комбинация  с этими с этими  является нулевым вектором V, т.е. является нулевым вектором V, т.е.  . Вектора . Вектора  , не являющиеся линейно зависимыми, называются линейно независимыми. Другими словами, , не являющиеся линейно зависимыми, называются линейно независимыми. Другими словами,  называются линейно независимыми, если их линейная комбинация является нулевым элементом V лишь при условии, что называются линейно независимыми, если их линейная комбинация является нулевым элементом V лишь при условии, что 
Определение 5. Совокупность векторов  называют базисом в называют базисом в  , если , если
1. вектора  – линейно независимы; – линейно независимы;
2. для  найдутся найдутся   . (1) . (1)
Определение 6. Линейное пространство  называется n–мерным, если называется n–мерным, если
1. В нем  n линейно независимых векторов. n линейно независимых векторов.
2.  векторов линейно зависимы. векторов линейно зависимы.
Определение 7.Линейное пространство называется бесконечномерным, если в нем  любое число линейно независимых векторов. любое число линейно независимых векторов.
Определение 6.Два произвольных линейных пространства V и  над одним и тем же полем над одним и тем же полем  называются изоморфными, если между элементами этих пространств можно установить взаимно-однозначное соответствие так, что если векторам называются изоморфными, если между элементами этих пространств можно установить взаимно-однозначное соответствие так, что если векторам  отвечают соответственные вектора отвечают соответственные вектора  , то вектору , то вектору  отвечает вектор отвечает вектор  , а вектору , а вектору  при при  отвечает вектор отвечает вектор  . .
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|


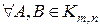 =>
=>  .
. =>
=>  .
. , где
, где  - нулевая матрица.
- нулевая матрица. . Матрица
. Матрица  называется противоположной к
называется противоположной к  и обозначается
и обозначается  .
. выполняется
выполняется .
. .
. .
. .
. =>
=>  .
. ,
,  .
. ,
,  .
. , где
, где  - единичная матрица.
- единичная матрица. .
. .
. .
. квадратных матриц
квадратных матриц  порядков
порядков  соответственно называется квадратная матрица
соответственно называется квадратная матрица  порядка
порядка  :
:  .
. .
. .
. .
. .
. порядка
порядка  с элементами из
с элементами из  называется элемент кольца
называется элемент кольца 
 =
=  =
=  ,
, множества из
множества из  – знак перестановки.
– знак перестановки. из
из  .
. Î
Î  называется транспонированной к матрице
называется транспонированной к матрице  –й столбец матрицы
–й столбец матрицы  называется транспонированием.
называется транспонированием.


 справедливо
справедливо 


 , то
, то  , если
, если  т.е.
т.е. 
 получена из
получена из  перестановкой каких–либо двух строк, то
перестановкой каких–либо двух строк, то 
 , то
, то  .
. .
. –ой строки матрицы
–ой строки матрицы  , то
, то  , где
, где  ,
,  имеют все строки, кроме
имеют все строки, кроме  , а
, а  , т.е.
, т.е.
 матрицы
матрицы  называется определитель матрицы порядка
называется определитель матрицы порядка  порядка
порядка  порядка
порядка  , элементы которого расположены на пересечении остальных строк и столбцов.
, элементы которого расположены на пересечении остальных строк и столбцов.

 , то
, то  равен сумме произведений элементов любой строки матрицы
равен сумме произведений элементов любой строки матрицы 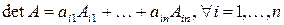 .
. называется обратной для
называется обратной для  .
. и вырожденной (особой), если
и вырожденной (особой), если  ,
, – алгебраическое дополнение элемента
– алгебраическое дополнение элемента  матрицы
матрицы  . Тогда
. Тогда





 является линейной комбинацией строк
является линейной комбинацией строк 
 , если для некоторых
, если для некоторых  справедливо
справедливо ,
,  (1)
(1) (1’)
(1’) назовем линейно зависимыми, если
назовем линейно зависимыми, если 
 такие
такие  одновременно не равные нулю, такие что
одновременно не равные нулю, такие что
 – линейно независимы, если равенство
– линейно независимы, если равенство 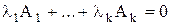 возможно лишь когда
возможно лишь когда  .
.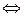 одна из этих строк является линейной комбинацией остальных.
одна из этих строк является линейной комбинацией остальных. называется рангом матрицы
называется рангом матрицы  , отличный от нуля.
, отличный от нуля. –го порядка равны нулю.
–го порядка равны нулю. вместе с заданными на нем операциями сложения векторов и умножения вектора на скаляр называется линейным (векторным) пространством над полем
вместе с заданными на нем операциями сложения векторов и умножения вектора на скаляр называется линейным (векторным) пространством над полем  , если удовлетворяются следующие аксиомы:
, если удовлетворяются следующие аксиомы: является абелевой группой;
является абелевой группой; и
и  выполняются равенства:
выполняются равенства: на
на  не изменяет
не изменяет  , т.е.
, т.е.  .
.

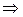
 .
.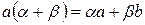 .
.

 .
. =>
=>  .
. =>
=>  .
. =>
=>  .
. =>
=>  .
. .
. .
. .
. с коэффициентами
с коэффициентами  называется выражение вида:
называется выражение вида:  .
. , из которых хотя бы одно отлично от нуля, т.е. линейная комбинация
, из которых хотя бы одно отлично от нуля, т.е. линейная комбинация  с этими
с этими  является нулевым вектором V, т.е.
является нулевым вектором V, т.е.  . Вектора
. Вектора 
 называют базисом в
называют базисом в  – линейно независимы;
– линейно независимы; найдутся
найдутся 
 . (1)
. (1) векторов линейно зависимы.
векторов линейно зависимы. над одним и тем же полем
над одним и тем же полем  отвечают соответственные вектора
отвечают соответственные вектора  , то вектору
, то вектору  отвечает вектор
отвечает вектор  , а вектору
, а вектору  при
при  отвечает вектор
отвечает вектор  .
.