Свойства рациональных дробей.
Комплексные числа
Комплексными числами называются упорядоченные пары  действительных чисел действительных чисел  и и  , если для них определены понятие равенства, операции сложения и умножения, удовлетворяющие следующим аксиомам: , если для них определены понятие равенства, операции сложения и умножения, удовлетворяющие следующим аксиомам:
1) Два числа  и и  равны тогда и только тогда, когда равны тогда и только тогда, когда  , ,  , т.е. , т.е.
2) Суммой комплексных чисел  и и  называется число, обозначаемое называется число, обозначаемое  и равное и равное  , т.е. , т.е.
3) Произведением комплексных чисел  и и  называется число, обозначаемое называется число, обозначаемое  и равное и равное 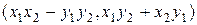 , т.е. , т.е.
Множество комплексных чисел обозначаетсяC. 
Комплексное число  называется сопряженным с комплексным числом называется сопряженным с комплексным числом  . .
Число  называется модулем комплексного числа называется модулем комплексного числа  и обозначается и обозначается  . .

| (4)
| Выражение (4) называется алгебраической формой записи комплексного числа.
 . .
| (6)
| Формулы (6) задают так называемую тригонометрическую форму записи комплексного числа.
Показательная форма записи комплексного числа:
 , где , где  , , 
Формула Муавра. Для  справедлива формула Муавра справедлива формула Муавра
 . .
Формула Эйлера

| (8)
| Корень n-ной степени из комплексного числа:

Алгебраические операции
Определение 1.  -арной алгебраической операцией на X называется отображение -арной алгебраической операцией на X называется отображение  . Т.е. . Т.е.   –компонентному элементу –компонентному элементу  однозначно ставится в соответствие элемент однозначно ставится в соответствие элемент  . .
Определение 2. Множество X с конкретной заданной на нем алгебраической операцией называется алгебраической структурой.
Определение 3. Бинарная операция  на X называется коммутативной, если на X называется коммутативной, если  ; ассоциативной, если ; ассоциативной, если  выполняется выполняется  . .
Определение 4. Элемент 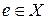 называется нейтральным относительно алгебраической операции называется нейтральным относительно алгебраической операции  , если , если
 . .
| (1)
| Определение 5.Множество  с заданной на нем бинарной ассоциативной операцией называется полугруппой. Полугруппа с нейтральным элементом называется моноидом или полугруппой с единицей. с заданной на нем бинарной ассоциативной операцией называется полугруппой. Полугруппа с нейтральным элементом называется моноидом или полугруппой с единицей.
Определение 6. Элемент  моноида моноида  называется симметричным к элементу называется симметричным к элементу  , если , если

| (2)
| Определение 7.Непустое множество G с заданной алгебраической операцией  называется группой, если называется группой, если
1)  – ассоциативная операция. – ассоциативная операция.
2) В G  нейтральный элемент нейтральный элемент  . .
3)   симметричный элемент из симметричный элемент из 
Если  – коммутативная операция, то группа называется коммутативной или абелевой. – коммутативная операция, то группа называется коммутативной или абелевой.
Свойства группы.
1) В группе G  нейтральный элемент и нейтральный элемент и   симметричный элемент. симметричный элемент.
2) Для  уравнения уравнения   имеют единственное решение: имеют единственное решение:
 , ,  . .
3) Закон сокращения в группе. Если  . .
Определение 8.Пусть  − произвольное множество из − произвольное множество из  элементов; например, элементов; например,  Перестановкой степени Перестановкой степени называетсявзаимно-однозначное отображение множества называетсявзаимно-однозначное отображение множества  в в  . .
Множество всех перестановок степени  обозначается обозначается  . .
 состоит из n!элементов. состоит из n!элементов.
Определение 9. Непустое множество K называется кольцом и обозначается (K  ), если выполняются условия: ), если выполняются условия:
1) (K, +) – абелева группа.
2) умножение ассоциативно, т.е. 
3) умножение дистрибутивно относительно сложения, т.е.
 , , 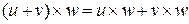 . .
Кольцо называется коммутативным, если умножение коммутативно. Если относительно умножения существует нейтральный элемент, то кольцо называется кольцом с единицей.
Свойства кольца.
1) Умножение дистрибутивно относительно вычитания, т.е.
 . .
2) 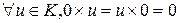 . .
3) Если  − отличный от нуля элемент из − отличный от нуля элемент из  , не являющийся делителем нуля, и , не являющийся делителем нуля, и  . Аналогично, . Аналогично, 
4) 
Определение 10. Множество  с заданными на нём алгебраическими операциями сложения + и умножения с заданными на нём алгебраическими операциями сложения + и умножения  называется полем и обозначается ( называется полем и обозначается (  ), если: ), если:
1) (P;+) – абелева группа.
2) (P\{0};  ) – абелева группа. ) – абелева группа.
3) Умножение дистрибутивно относительно сложения, т.е.

Свойства поля.
1) В поле Р нет делителей нуля.
2) Сокращение на ненулевой элемент:  из из  
3)  , уравнение , уравнение  в поле P имеет единственное решение в поле P имеет единственное решение  . .
Определение 11.Пусть  (композиция) − бинарная алгебраическая операция на (композиция) − бинарная алгебраическая операция на 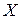 . Подмножество . Подмножество 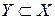 называется замкнутым относительно называется замкнутым относительно  , если , если  выполняется выполняется 
Определение 18. Пусть 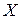 и и  − множества, − множества,  и и  − бинарные операции (на − бинарные операции (на 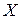 и и  соответственно). Гомоморфизмом из соответственно). Гомоморфизмом из  в в  называется отображение называется отображение  такое, что такое, что 
Пример. Отображение  является гомоморфизмом из (R, +) в (R, является гомоморфизмом из (R, +) в (R, 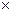 ). Это следует из справедливости равенства ). Это следует из справедливости равенства 
Определение 19.Изоморфизм − это биективный гомоморфизм.
Определение 20. Пара  изоморфна паре изоморфна паре  , если , если  изоморфизм из изоморфизм из  в в  . .
Многочлены
Пусть  – поле. Тогда многочленом (полиномом) от одной переменной – поле. Тогда многочленом (полиномом) от одной переменной  с коэффициентами из с коэффициентами из  называется выражение вида называется выражение вида

Определение 1. Многочленом одной переменной с коэффициентами из  называется бесконечная последовательность называется бесконечная последовательность  , в которой лишь конечное число элементов не равно нулю. , в которой лишь конечное число элементов не равно нулю.
Множество многочленов с коэффициентами из поля  обознается обознается  . .
Сложение умножение многочленов.
Пусть  . Тогда . Тогда
 , ,  , где , где  . .
Деление многочленов.
Теорема 2. Пусть  . Тогда . Тогда 
 и и  . .
| (1)
| Определение 2.Если 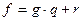 и и  , то , то  называется остатком при делении называется остатком при делении  на на 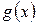 . .
Определение 3. Пусть  . Если . Если    , то говорят, что , то говорят, что  делится на делится на 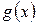 или или 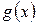 делит делит  , и пишут , и пишут  . Если . Если  , то , то  означает, что остаток от деления равен означает, что остаток от деления равен  . В этом случае многочлен . В этом случае многочлен 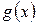 называется делителем многочлена называется делителем многочлена  . .
Свойства (делимости многочленов). Пусть  , , 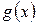 , ,  , ,  , ,  , ,  . Тогда справедливы свойства: . Тогда справедливы свойства:
1) Если  , ,  . .
2)  , ,  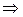  . .
3)  , ,  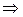  . .
4)  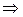   выполняется выполняется  . .
5) Если  , , 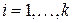 , то справедливо , то справедливо
 . .
6)  . .
7)  имеем имеем  . .
8) 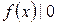 . .
9)  . .
10)  . .
11) Если 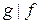 , то , то  имеем имеем 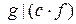 . .
Определение 4. Многочлен  называется общим делителем называется общим делителем  и и  , если , если  и и  . Наибольшим общим делителем (НОД) двух многочленов . Наибольшим общим делителем (НОД) двух многочленов  и и 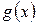 называется их делитель называется их делитель  , который делится на любой другой их общий делитель. , который делится на любой другой их общий делитель.
Определение 5. Многочлены  называют взаимно простыми, если их общими делителями являются только многочлены нулевой степени. называют взаимно простыми, если их общими делителями являются только многочлены нулевой степени.
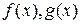 – взаимно просты – взаимно просты 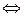 НОД НОД  . .
Определение 6. Число  называется корнем многочлена называется корнем многочлена 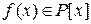 , если , если  . .
Теорема 6 (теорема Безу). Пусть 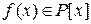 . Тогда . Тогда  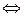 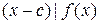 . .
Доказательство.Разделим  на на  : :  , где , где  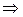  const. Тогда const. Тогда  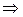 
 . ■ . ■
Определение 7. Наибольшее  называется кратностью корня называется кратностью корня  многочлена многочлена  . Такой корень . Такой корень  называется называется  -кратным корнем -кратным корнем  Если Если  , то корень называется простым. , то корень называется простым.
Теорема 8 (ОТА). Всякий многочлен  , имеет хотя бы один комплексный корень. , имеет хотя бы один комплексный корень.
Интерполяционный многочлен Лагранжа.
Для любых попарно различных  и любых и любых  существует единственный многочлен существует единственный многочлен 
Такой многочлен имеет вид:
 , (5) , (5)
где 
Из формулы видно, что  и так как и так как
 , то , то 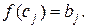
Определение 8.Построенный многочлен  называется интерполяционным многочленом Лагранжа, а (5) – интерполяционной формулой Лагранжа. называется интерполяционным многочленом Лагранжа, а (5) – интерполяционной формулой Лагранжа.
Определение 9. Многочлен  , называется неприводимым (над полем , называется неприводимым (над полем  ), если его нельзя представить в виде произведения многочленов из ), если его нельзя представить в виде произведения многочленов из  , степени которых меньше , степени которых меньше  . .
Рациональные дроби
Пусть  – поле, – поле,  – кольцо многочленов над – кольцо многочленов над  . .
Определение 1.Если задана пара многочленов  , где , где  , то символ , то символ  называется рациональной дробью с числителем называется рациональной дробью с числителем  и знаменателем и знаменателем  . .
Определение 2.Рациональные дроби  и и  называются равными, если в кольце называются равными, если в кольце  имеется равенство имеется равенство
 . .
| (1)
|
Свойства рациональных дробей.
1.  дробь равна самой себе. дробь равна самой себе.
2. Свойство транзитивности: если  и и  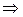  . .
Определение 3.Рациональная дробь называется правильной, если степень числителя меньше степени знаменателя.
Определение 4. Правильная рациональная дробь  называется простейшей, если её знаменатель называется простейшей, если её знаменатель  является степенью неприводимого многочлена является степенью неприводимого многочлена 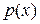 , т.е. , т.е.  , и , и  . .
Пример. Представим  в виде суммы простейших дробей, где в виде суммы простейших дробей, где
 . .
Здесь  и значит разложение дроби и значит разложение дроби  на суму простейших имеет вид на суму простейших имеет вид 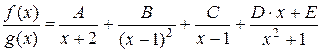 . .
Тогда искомое разложение имеет вид:
 . .
Матрицы и определители
Пусть  – коммутативное кольцо с единицей. – коммутативное кольцо с единицей.
Определение 1. Матрицей размеров 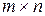 над кольцом над кольцом  называется прямоугольная таблица из называется прямоугольная таблица из  элементов кольца элементов кольца  и имеющая и имеющая  строк и строк и  столбцов: столбцов:

где  – номер строки, – номер строки,  – номер столбца, – номер столбца,  − элементы матрицы, − элементы матрицы,  и и  − порядки матрицы. В этом случае говорят, рассматриваемая матрица размера − порядки матрицы. В этом случае говорят, рассматриваемая матрица размера 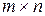 . Если . Если  , то матрица называется квадратной, а число , то матрица называется квадратной, а число  – её порядком. – её порядком.
Определение 2. Две матрицы называются равными, если эти матрицы имеют одинаковые порядки и их соответствующие элементы совпадают.
Определение 3. Суммой  матриц матриц  и и  (т.е. имеющих одинаковые порядки) называется матрица (т.е. имеющих одинаковые порядки) называется матрица  : :  . .
Определение 4. Произведением  элемента элемента  на матрицу на матрицу  называется матрица называется матрица 
Определение 5.Произведением  матриц матриц  размера размера 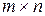 и и  размера размера  называется матрица называется матрица  размеров размеров 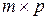 такая, что каждый элемент такая, что каждый элемент 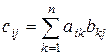 . .
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|


 действительных чисел
действительных чисел  и
и  , если для них определены понятие равенства, операции сложения и умножения, удовлетворяющие следующим аксиомам:
, если для них определены понятие равенства, операции сложения и умножения, удовлетворяющие следующим аксиомам: и
и  равны тогда и только тогда, когда
равны тогда и только тогда, когда  ,
,  , т.е.
, т.е. Û
Û  ,
, 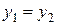 .
.
 и равное
и равное  , т.е.
, т.е.
 +
+  =
=  .
.
 и равное
и равное 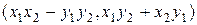 , т.е.
, т.е.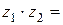
 ∙
∙  =
=  .
.

 называется сопряженным с комплексным числом
называется сопряженным с комплексным числом  .
. называется модулем комплексного числа
называется модулем комплексного числа  и обозначается
и обозначается  .
.
 .
.
 , где
, где  ,
, 
 справедлива формула Муавра
справедлива формула Муавра .
.

 -арной алгебраической операцией на X называется отображение
-арной алгебраической операцией на X называется отображение  . Т.е.
. Т.е. 
 однозначно ставится в соответствие элемент
однозначно ставится в соответствие элемент  .
. на X называется коммутативной, если
на X называется коммутативной, если  ; ассоциативной, если
; ассоциативной, если  выполняется
выполняется  .
.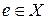 называется нейтральным относительно алгебраической операции
называется нейтральным относительно алгебраической операции  , если
, если .
.
 с заданной на нем бинарной ассоциативной операцией называется полугруппой. Полугруппа с нейтральным элементом называется моноидом или полугруппой с единицей.
с заданной на нем бинарной ассоциативной операцией называется полугруппой. Полугруппа с нейтральным элементом называется моноидом или полугруппой с единицей. называется симметричным к элементу
называется симметричным к элементу  , если
, если
 нейтральный элемент
нейтральный элемент  .
.

 нейтральный элемент и
нейтральный элемент и  уравнения
уравнения 
 имеют единственное решение:
имеют единственное решение: ,
,  .
. .
. − произвольное множество из
− произвольное множество из  Перестановкой степени
Перестановкой степени .
. ), если выполняются условия:
), если выполняются условия:
 ,
, 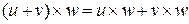 .
. .
.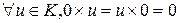 .
. − отличный от нуля элемент из
− отличный от нуля элемент из  , не являющийся делителем нуля, и
, не являющийся делителем нуля, и  . Аналогично,
. Аналогично, 

 с заданными на нём алгебраическими операциями сложения + и умножения
с заданными на нём алгебраическими операциями сложения + и умножения  называется полем и обозначается (
называется полем и обозначается (  ), если:
), если:
 из
из 

 , уравнение
, уравнение  в поле P имеет единственное решение
в поле P имеет единственное решение  .
.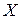 . Подмножество
. Подмножество 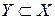 называется замкнутым относительно
называется замкнутым относительно  выполняется
выполняется 
 − множества,
− множества,  в
в  называется отображение
называется отображение  такое, что
такое, что 
 является гомоморфизмом из (R, +) в (R,
является гомоморфизмом из (R, +) в (R, 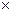 ). Это следует из справедливости равенства
). Это следует из справедливости равенства 

 , в которой лишь конечное число элементов не равно нулю.
, в которой лишь конечное число элементов не равно нулю. .
. . Тогда
. Тогда ,
,  , где
, где  .
. . Тогда
. Тогда 
 и
и  .
.
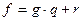 и
и  , то
, то  называется остатком при делении
называется остатком при делении  на
на 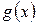 .
. . Если
. Если 
 , то говорят, что
, то говорят, что  . Если
. Если  , то
, то  . В этом случае многочлен
. В этом случае многочлен  ,
,  ,
,  ,
,  . Тогда справедливы свойства:
. Тогда справедливы свойства: .
. ,
, 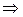
 .
. .
. выполняется
выполняется  .
. ,
, 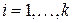 , то справедливо
, то справедливо .
. .
. имеем
имеем  .
.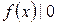 .
. .
. .
.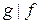 , то
, то  имеем
имеем 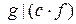 .
. называется общим делителем
называется общим делителем  , если
, если  и
и  . Наибольшим общим делителем (НОД) двух многочленов
. Наибольшим общим делителем (НОД) двух многочленов  , который делится на любой другой их общий делитель.
, который делится на любой другой их общий делитель. называют взаимно простыми, если их общими делителями являются только многочлены нулевой степени.
называют взаимно простыми, если их общими делителями являются только многочлены нулевой степени.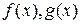 – взаимно просты
– взаимно просты 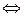 НОД
НОД  .
. называется корнем многочлена
называется корнем многочлена 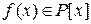 , если
, если  .
.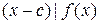 .
. на
на  :
:  , где
, где 
 const. Тогда
const. Тогда 

 . ■
. ■ называется кратностью корня
называется кратностью корня  многочлена
многочлена  -кратным корнем
-кратным корнем  Если
Если  , то корень называется простым.
, то корень называется простым. , имеет хотя бы один комплексный корень.
, имеет хотя бы один комплексный корень. и любых
и любых  существует единственный многочлен
существует единственный многочлен 
 , (5)
, (5)
 и так как
и так как , то
, то 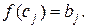
 , называется неприводимым (над полем
, называется неприводимым (над полем  , где
, где  , то символ
, то символ  называется рациональной дробью с числителем
называется рациональной дробью с числителем  .
. называются равными, если в кольце
называются равными, если в кольце  .
.
 и
и 
 .
.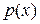 , т.е.
, т.е.  , и
, и  .
. .
. и значит разложение дроби
и значит разложение дроби 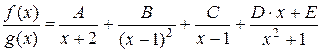 .
. .
.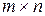 над кольцом
над кольцом  элементов кольца
элементов кольца  строк и
строк и 
 – номер строки,
– номер строки,  – номер столбца,
– номер столбца,  − элементы матрицы,
− элементы матрицы,  , то матрица называется квадратной, а число
, то матрица называется квадратной, а число  матриц
матриц  и
и  (т.е. имеющих одинаковые порядки) называется матрица
(т.е. имеющих одинаковые порядки) называется матрица  :
:  .
. элемента
элемента  на матрицу
на матрицу  называется матрица
называется матрица 
 матриц
матриц  размера
размера  размера
размера  называется матрица
называется матрица  размеров
размеров 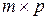 такая, что каждый элемент
такая, что каждый элемент 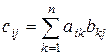 .
.