
|
|
Свойства изоморфных пространств.1. Нулевому элементу V соответствует нулевой элемент 2. Если элементам 3. Если V и 4. Пространства разных размерностей не могут быть изоморфными. Определение 1.Непустое подмножество 1. 2. Определение 2.Линейной оболочкой
где Определение 3.Элементарными преобразованиями матрицы называются следующие преобразования: 1. Умножение строки на элемент 2. Прибавление к одной строке другой строки. 3. Перестановка строк. 4. Такие же преобразования над столбцами. Определение 6.Будем называть суммой подпространств Определение 7.Назовём пересечением подпространств Теорема 6.Сумма размерностей произвольных подпространств Определение 8.Будем говорить, что векторное пространство Системы линейных уравнений Определение 1.Системой
где Определение 2.Совокупность Определение 3.Если система (1) имеет хотя бы одно решение, то она называется совместной, если решений нет – несовместной. Теорема 1. (правило Крамера) Система
где Теорема 2. (теорема Кронекерра–Капелли). Для того чтобы система (1) была совместной, необходимо и достаточно, чтобы ранг ее расширенной матрицы был равен рангу основной матрицы, т.е.
Определение 9. Всякая линейно независимая система Геометрические вектора Рассмотрим в пространстве две точки А и В. Они определяют отрезок АВ. Определение 1.Отрезок АВ называется направленным, если его концы А и В упорядочены; если при этом первой является точка А, а второй – точка В, то А – начало отрезка, а В – его конец. Направленный отрезок обозначается Определение 4.Два направленных отрезка Определение 5.Множество всех эквивалентных направленных отрезков называется вектором (или свободным вектором). Определение 7.Два ненулевых вектора, направления которых совпадают или противоположны, называются коллинеарными. Обозначают Определение 8.Три и более векторов называются компланарными, если они параллельны некоторой плоскости. Свойства сложения векторов. 1. 2. 3. 4. Для каждого вектора Определение 10.Произведением вектора 1) векторы 2) 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 и наоборот.
и наоборот.
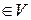 соответствуют
соответствуют  , то линейная комбинация векторов
, то линейная комбинация векторов  линейная комбинация
линейная комбинация  с теми же коэффициентами
с теми же коэффициентами  равна нулю, т.е.
равна нулю, т.е. 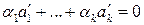 .
. векторного пространства
векторного пространства  над полем
над полем  называется линейным подпространством (или просто подпространством) линейного пространства
называется линейным подпространством (или просто подпространством) линейного пространства  , их сумма
, их сумма  .
. ,
,  , имеем:
, имеем:  .
. множества
множества  (линейной оболочкой
(линейной оболочкой  ) будем называть совокупность всех линейных комбинаций этих элементов, т.е. множество элементов вида
) будем называть совокупность всех линейных комбинаций этих элементов, т.е. множество элементов вида ,
, – произвольные элементы
– произвольные элементы  , отличный от нуля.
, отличный от нуля.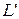 и
и  и обозначать
и обозначать  множество всех векторов, которые можно представить в виде
множество всех векторов, которые можно представить в виде  , где
, где  и
и  .
. множество векторов, котоые принадлежат одновременно обоим подпространствам.
множество векторов, котоые принадлежат одновременно обоим подпространствам. .
. подпространств
подпространств 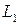 и
и  , если
, если  может быть единственным образом представлен в виде суммы
может быть единственным образом представлен в виде суммы 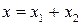 , где
, где  ,
,  .
. линейных уравнений с
линейных уравнений с  неизвестными
неизвестными  над полем
над полем 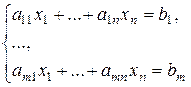 (1)
(1)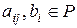 . Элементы
. Элементы  называются коэффициентами системы (1),
называются коэффициентами системы (1),  – ее свободные члены. Если все
– ее свободные члены. Если все  , то система (1) называется однородной, иначе – неоднородной.
, то система (1) называется однородной, иначе – неоднородной. называется решением (1), если после подстановки их вместо
называется решением (1), если после подстановки их вместо  соответственно во все уравнения (1) получаются тождества.
соответственно во все уравнения (1) получаются тождества.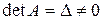 , имеет решение, причем только одно. Это решение находится по формулам:
, имеет решение, причем только одно. Это решение находится по формулам: ,
, 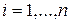 , (3)
, (3) ,
,  – определитель матрицы, получаемой из
– определитель матрицы, получаемой из  заменой
заменой 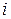 -ого столбца на столбец свободных членов.
-ого столбца на столбец свободных членов. .
. решений СЛОУ (1) называется фундаментальной системой решений.
решений СЛОУ (1) называется фундаментальной системой решений. .
. считаются эквивалентными, если они сонаправлены и имеют равные длины. (Обозначают
считаются эквивалентными, если они сонаправлены и имеют равные длины. (Обозначают  ).
). .
. .
. .
. , т.к.
, т.к. 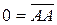 .
.
 вектор, называемый вектором, противоположным
вектор, называемый вектором, противоположным  .
.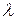
 называется вектор
называется вектор 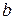 , удовлетворяющий следующим условиям:
, удовлетворяющий следующим условиям: и противоположно направлены, если
и противоположно направлены, если  ;
; .
.