
|
|
Решение на основе графического моделирования
А В
А В
А В
Ответ:1 час
Рассмотрим задания с физическим содержанием, предлагаемое на ЕГЭ по математике в 2010 году. Это задания типа В12 из I части экзаменационной работы. Задача №1.Расстояние между пристанями А и В равно 48 км. Отчалив от пристани А в 10 часов утра, теплоход проплыл по течению реки с постоянной скоростью до пристани В. После трехчасовой стоянки у пристани В теплоход отправился в обратный рейс и прибыл в пункт А в тот же тень в 22.00. Найдите скорость теплохода в неподвижной воде, если скорость течения реки равна 4 км/ч. Решение Пусть
Пусть
Задача №2. Первую половину трассы автомобиль проехал со скоростью 38 км/ч, а вторую – со скоростью 57 км/ч. Найдите среднюю скорость на протяжении всего пути.
Решение
Время движения автомобиля на первом участке -
Время движения автомобиля на втором участке -
Все время движения:
Средняя скорость автомобиля на всем пути
Ответ: Задача №3. Два автомобиля отправляются в 780-километроный пробег. Первый едет со скоростью на 13 км/ч большей, чем второй, и прибывает к финишу на 2 часа раньше второго. Найдите скорость автомобиля, пришедшего к финишу первым. Ответ дайте в км/ч. Решение:
Воспользуемся формулой
Первый автомобиль был в пути на 2 часа меньше, чем второй: Составим уравнение, учитывая, что
Ответ: Задача №4. Из пункта А в пункт В вниз по течению реки отправились одновременно моторная лодка и байдарка. Скорость течения реки равна 3 км/ч. Последнюю Решение. Пусть t время движения моторной лодки и байдарки из пункта А в пункт В
На первом участке На втором участке
Решая квадратное уравнение, получим Ответ: Задача №5. Велосипедист отправился с некоторой скоростью из города А в город В, расстояние между которыми равно 88 км. Возвращаясь из В в А, он ехал поначалу с той же скоростью, но через 1 час пути вынужден был сделать остановку на 15 мин. После он продолжил путь в А, увеличив скорость на 2 км/ч, и в результате затратив на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В.
В заключение хотелось бы отметить, что работа с текстами физического содержания требует от учителя и учащихся особых умений: · Понимать смысл перечисляемых в тексте терминов; · Отвечать на прямые вопросы к содержанию текста; · Отвечать на вопросы, требующие сопоставления информации из различных частей текста; · Использовать информацию из текста в измененной ситуации; · Переводить информацию из одной знаковой системы в другую. Решение задач на основе графического моделирования позволяет ученику представить учебную задачу как систему ярких опорных образов, а затем осмысленно решить.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

 Автомобиль выехал на 1 час раньше, чем мотоциклист.
Автомобиль выехал на 1 час раньше, чем мотоциклист.
 А В
А В









 А В
А В

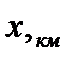
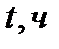






 0 1 2 3 4
0 1 2 3 4

 Автомобиль прибыл в пункт В через 4 часа после начала движения, мотоциклист - на 1 час раньше:
Автомобиль прибыл в пункт В через 4 часа после начала движения, мотоциклист - на 1 час раньше: -время движения теплохода по течению реки из пункта А в пункт В
-время движения теплохода по течению реки из пункта А в пункт В






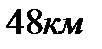
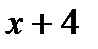





 - время стоянки в пункте В
- время стоянки в пункте В -время движения теплохода против течения реки из пункта В в пункт А
-время движения теплохода против течения реки из пункта В в пункт А



 Все время движения составило
Все время движения составило 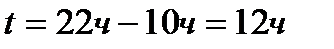
 Или
Или 

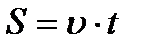 Воспользуемся формулой
Воспользуемся формулой Время движения теплохода из пункта
Время движения теплохода из пункта

 А в пункт В -
А в пункт В -



 Время движения теплохода из пункта В в пункт А -
Время движения теплохода из пункта В в пункт А -



 Решая квадратное уравнение, получим
Решая квадратное уравнение, получим  .
Ответ:
.
Ответ: 




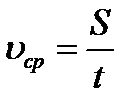
 Найдем среднюю скорость автомобиля
Найдем среднюю скорость автомобиля где
где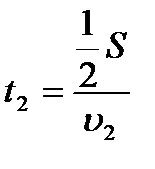

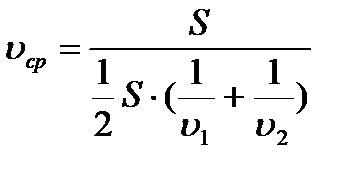











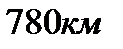
 Время движения первого автомобиля -
Время движения первого автомобиля -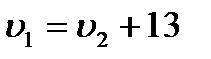
 , решая которое получим
, решая которое получим 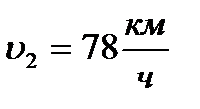
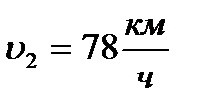
 часть пути моторная лодка шла с выключенным мотором, и ее скорость относительно берега была равна скорости течения реки. На той части пути, где моторная лодка шла с включенным мотором, ее скорость была на 2 км/ч больше скорости байдарки. Найдите скорость байдарки в неподвижной воде, если в пункт В байдарка и моторная лодка прибыли одновременно.
часть пути моторная лодка шла с выключенным мотором, и ее скорость относительно берега была равна скорости течения реки. На той части пути, где моторная лодка шла с включенным мотором, ее скорость была на 2 км/ч больше скорости байдарки. Найдите скорость байдарки в неподвижной воде, если в пункт В байдарка и моторная лодка прибыли одновременно.

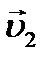








 моторная лодка двигалась со скоростью
моторная лодка двигалась со скоростью 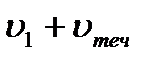
 моторная лодка, двигалась с выключенным мотором
моторная лодка, двигалась с выключенным мотором со скоростью
со скоростью 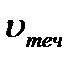




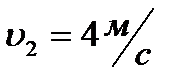















 А в пункт В -
А в пункт В -





 Подставим в формулу выражения и
Подставим в формулу выражения и
 и
и  , получим
, получим

 Решая квадратное уравнение, получим
Решая квадратное уравнение, получим  .
Ответ:
.
Ответ: 