
|
|
Иррациональные уравнения.Иррациональным уравнением называется уравнение, левая и правая части которого являются алгебраическими выражениями, причём хотя бы в одном из них под знаком корня содержится неизвестное. Иррациональное уравнение может иметь как конечное, так и бесконечное число решений, может и вовсе не иметь решений. Все радикалы, входящие в иррациональное уравнение, рассматриваются только как арифметические. Область определения иррационального уравнения состоит из тех значений неизвестного, при которых все выражения, стоящие под знаками радикалов чётных степеней, одновременно являются неотрицательными величинами. Существуют различные методы решения иррациональных уравнений: 1) Возведения уравнений в степень. 2) Введение вспомогательных неизвестных величин, 3) Умножение обеих частей уравнения на некоторую функцию. Примеры: а) Возведя обе части данного уравнения в квадрат, получим уравнение: 2х2+5х-3=х+1. Область определения: Решаем полученное уравнение и систему неравенств:
Корни уравнения: х1=-4. Х2=1, область определения:
Отсюда следует, что решением уравнения является только х=1. б) Решить уравнение Оставляем в левой части только радикал
Область определения уравнения 2+х 2-х Возводим обе части уравнения в квадрат: Х+2=4-4х+х2; Х2-5х+2=0. Последнему уравнению удовлетворяют два значения неизвестного: Х1= Так как область определения уравнения -2 в) Решить уравнение Возводим обе части уравнения в квадрат: Х+2+2
Снова возводим в квадрат обе части уравнения:
16х=-16; Х=-1. Проверка подтверждает, что значение х=-1 является корнем.
Уравнения с модулем.
Уравнения с модулем – уравнения вида f( Специальные виды уравнений. Биквадратное уравнение имеет вид: ах4 + вх2+с=0, а Заменой неизвестного х2=у уравнение приводится к квадратному Корни биквадратного уравнения : х1,2,3,4= Свойства биквадратного уравнения: 1) Если биквадратное уравнение имеет корень 2) Сумма биквадратного уравнения равна нулю. Задание 9. 1. Решить линейные уравнения: 1) 2) 3) 4) 5) 6)
2. Решить квадратные уравнения: 1) 0,04х2-0,64=0; 2) 4х2-0,81=0; 3) х(х-3)=4х-6х2; 4) 3х2+4х=2(х2-3х); 5) 6) 7) 8) 9) 10) х(2х+1=3х+4; 11) х(2х-3)+4х-3; 12) (10х-4)(3х+2)=0; 13) 6(10-х)(3х+4)=0; 14) 2(5х-7)(1+х)=0; 15) 16) 3. Решить дробно- рациональные уравнения: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12)
4. Решить иррациональные уравнения: 1) х + 2) х+ 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15)
5. Решить уравнения с неизвестным под знаком модуля: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15)
1) 2) 3) 2х4-100х2+98=0; 4) 3х4-51х2+48=0; 5) 100х4-13х2+0,36=0; 6) 2х4-100х2+98=0.
5.Решить уравнения методом замены переменной: 1) (х2+5х+8)2-6(х2+5х+8)+8=0; 2) (х2-3х)2-2(х2+4х-17)+60=0; 3) (х2-5х)(х2-5х+10)+24=0; 4) (х2-3х)2-2(х2-3х)=8; 5) (х2+х)2-11(х2+х)=12; 6) 7) 3 8)
Самостоятельная работа: 1. Решить системы линейных уравнений: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14)
2. Решить системы квадратных уравнений: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15)
Неравенства, системы неравенств. Неравенства с одним неизвестным имеют вид f(x) Основные методы решения неравенств: 1. Метод интервалов основан на следующем свойстве функций: если функция непрерывна в промежутке и между этими точками она корней не имеет, то в этом промежутке функция сохраняет знак. На числовой оси отмечают все точки, в которых функция обращается в нуль, либо не определена. Эти точки разбивают числовую прямую на промежутки, в которых функция непрерывна и сохраняет знак. Для определения знака используется метод пробной точки. 2. Метод замены переменного в неравенствах. Если неравенство может быть преобразовано к виду f(g(x)) 3. Метод используется в случаях, когда неравенство допускает простую геометрическую интерпретацию. Рациональные неравенства. Алгоритм решения рационального неравенства следующий: !. Переносят все слагаемые в левую часть неравенства. 2.Приводят (если требуется) дроби к общему знаменателю. 3. Раскладывают числитель и знаменатель на множители. 4. Применяют метод интервалов. Пример: Решить неравенство
На интервале - Ответ: 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 .
.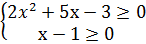

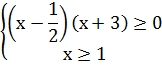
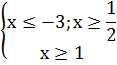
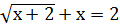 .
. .
.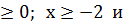
 ; х
; х 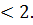
 ; х2=
; х2=  .
. х=
х=  .
. ;
; – х.
– х.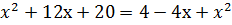 ;
; .
. ,
, 
 . Для решения таких уравнений применяют метод промежутков. Для этого находят область определения уравнения и находят корни совокупности уравнений. Внутри каждого из промежутков, на которые найденные точки разбивают область определения уравнения, выражения, стоящие под знаком модуля, имеют постоянный знак. Поэтому исходное уравнение на каждом промежутке заменяют на равносильное уравнение, не содержащее знака модуля.
. Для решения таких уравнений применяют метод промежутков. Для этого находят область определения уравнения и находят корни совокупности уравнений. Внутри каждого из промежутков, на которые найденные точки разбивают область определения уравнения, выражения, стоящие под знаком модуля, имеют постоянный знак. Поэтому исходное уравнение на каждом промежутке заменяют на равносильное уравнение, не содержащее знака модуля. .
. .
.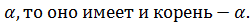
 ;
; ;
; ;
;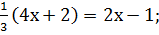
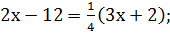
 .
. ;
; ;
;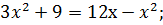
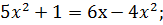
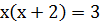
 ;
; .
. ;
;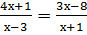 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
;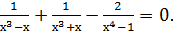
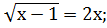
 ;
;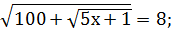
 =11;
=11; ;
; ;
; ;
; ;
; ;
;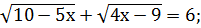
 ;
; =28;
=28; ;
; ;
; .
. ;
; ;
; ;
; ;
;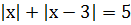 ;
;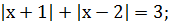
 ;
; ;
; ;
; ;
; ;
;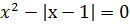 ;
; ;
; ;
; .
.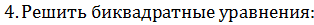
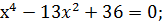
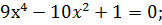
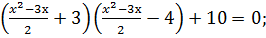
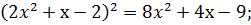
 ;
; .
.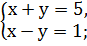
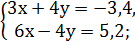
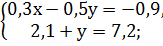
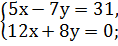
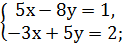
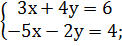
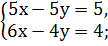

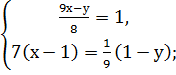
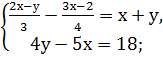
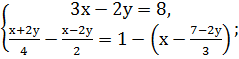
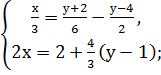
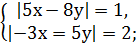
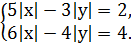
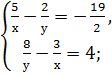
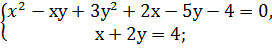

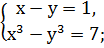
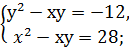
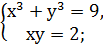

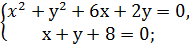
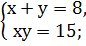
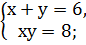
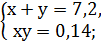
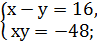
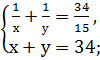
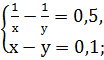
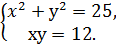
 , или f
, или f  , или
, или  ,или
,или 
 .
. ;
; .
. в точке х=0 ив точке х =
в точке х=0 ив точке х =  она не определена.
она не определена.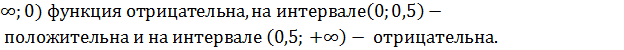
 .
.