
|
|
Обращение десятичной дроби в простую дробьИ простую в десятичную. Чтобы обратить десятичную дробь в простую, число, стоящее после запятой, пишут в числителе, а в знаменателе пишут 10к, где к – число цифр справ от запятой. Чтобы простую дробь обратить в десятичную дробь, числитель простой дроби делят её на знаменатель по правилу деления десятичной дроби на целое число. При обращении простой дроби в десятичную дробь может образоваться бесконечная десятичная дробь.
Проценты. Процент – сотая часть числа. Если число принято за единицу, то 1% его составляет 0,01этого числа. Выражение величины а в процентах другой величины b P= Называется процентным отношением чисел а и b. Если величина а составляет p% величины b,то a= Типы задач на проценты: 1) Отыскание всего числа по заданной величине его процента; 2) Отыскание заданного процента от данного числа; 3) Отыскание процентного отношения двух чисел.
Пропорции Пропорцией называется равенство двух отношений:
Члены a и b пропорции называются крайними c и d - средними. Свойства пропорций: 1) Произведение её крайних членов равно произведению средних членов; a 2) Каждый её крайний член равен произведению средних, делённому на другой крайний; a= 3) Каждый её средний член равен произведению крайних, делённому на другой средний; b= 4) В каждой пропорции можно менять местами или только средние члены, или только крайние, или и те и другие одновременно.
Задание !. 1. Выполнить действия: 1) 1 2) (6 3) 12 4) (0,5+ 5) 45,09 :1,5-(2 6) 0,364: 7) 8) 9) 10) 11) 12) 13) 14)
2. Найти: 1) 8% от20,4 т; 2) 3) 4)
3. Найти число, если 1) 42% его составляет 6,3; 2) 12% его составляет 30; 3) 45% его составляет 30; 4) 170% его составляет 510; 5) 3% его составляет 9,6; 6) 130% его составляет 6,5; 7) 6,2% его составляет 1,6.
4. Найти 1) 15% от 45,09:1,5- 2) 15% от 3) 37% от
5. Найти неизвестный член пропорции: 1) 9 2) 4х: 3) 2,5:0,125=0,5х:0,75; 4) 10:0,01=
Комплексные числа. Определение комплексного числа. Итальянские математики Дж. Кордано и Р.Бомбелли, решая квадратные уравнения вида х2+а2=0,ввели в рассмотрение символ Комплексным числом называется выражение вида а+bi? где i2=-1. Число а называется действительной частью, bi – мнимой частью, i – мнимой единицей. Два комплексных числа называются равными, если равны соответственно их действительные и мнимые части. Комплексные числа с равными действительными частями и противоположными по знаку мнимыми частями называются комплексно-сопряжёнными. Геометрически комплексное число а+bi можно представить точкой координатной плоскости с координатами а,в. Плоскость, служащая для изображения множества комплексных чисел, называется комплексной плоскостью. Ось ОХ называется действительной осью, а ось ОУ – мнимой осью. Из определения комплексно-сопряжённых чисел следует, что на комплексной плоскости они расположены симметрично относительно действительной оси. Квадратное уравнение ах2+вх +с+0, для которого дискриминант отрицателен, будет иметь два комплексно -сопряжённых корня Пример: Решить уравнение 2х2-6х+9=0. Находим: х= Действия над комплексными числами. Действия над комплексными числами определяются таким образом, что для частного случая действительных чисел эти операции совпадали с известными операциями над ними. Пусть даны два комплексных числа: z1= a1+b1i , z2= a2 +b2i. Сумма комплексных чисел определяется: z1 + z2 = (a1+b1i) + (a2 +b2i) = (а1 + а2 ) + (b1 + b2)i. Вычитание двух комплексных чисел определяется как операция, обратная сложению: z1 - z2 = (a1+b1i) - (a2 +b2i) = (а1 - а2 ) + (b1 - b2)i. Умножение двух комплексных чисел определяетс z1 Деление комплексных чисел определяется: Z1/Z2=(a1+b1i)/(a2+b2i) = (a1+b1i)(a2-b2i) /(a2+b2i) (a2-b2i) =(а1 а2 + b1 b2 )/(a2+b2) +(a2b1-a1b2)/ (a2+b2). Пример : Даны числа 2+3i и 1-2i. Найти сумму, разность. произведение и частное этих чисел. 1) (2+3i) +( 1-2i) = 2+3i + 1-2i = 3+i 2) (2+3i) -( 1-2i) = 2+3i- 1+2i = 1+5i 3) (2+3i) 4) (2+3i):( 1-2i) = (2+3i)
Задание 2. Вариант1. 1.Решить квадратное уравнение: х2+2х+5=0 2. Даны числа: 17-6i; 3-4i. Вычислить сумму, разность, произведение и частное этих чисел.
Вариант2. 1.Решить квадратное уравнение: x2-6x+18=0 2. Даны числа: 4-3i; 2+i. Вычислить сумму, разность, произведение и частное этих чисел.
Вариант3. 1.Решить квадратное уравнение: x2-4x +5=0 2. Даны числа: 3-I; 3+i. Вычислить сумму, разность, произведение и частное этих чисел.
Вариант4. 1.Решить квадратное уравнение: x2-10x+41 =0 2. Даны числа: -2+5i; 3-4i. Вычислить сумму, разность, произведение и частное этих чисел. Вариант5 1.Решить квадратное уравнение: х2-14х+50=0 2. Даны числа: 5-3i; -1+6i. Вычислить сумму, разность, произведение и частное этих чисел. Вариант 6. 1.Решить квадратное уравнение: х2-4х +53=0 2. Даны числа: 0,2+4i; 0,3-0,9i Вычислить сумму, разность, произведение и частное этих чисел.
Вариант 7. 1.Решить квадратное уравнение: х2+4х+53=0 2. Даны числа: 2+2i 1-4i Вычислить сумму, разность, произведение и частное этих чисел.
Вариант8. 1.Решить квадратное уравнение: х2+2х+50=0 2. Даны числа: 5-3i; -4+7i Вычислить сумму, разность, произведение и частное этих чисел.
Вариант 9. 1.Решить квадратное уравнение: х2-2х+50 =0 2. Даны числа: 4-2i; 1-i Вычислить сумму, разность, произведение и частное этих чисел.
Вариант 10. 1.Решить квадратное уравнение: х2+10х+26=0 2. Даны числа: 2-I; 3+4i Вычислить сумму, разность, произведение и частное этих чисел. Вариант11. 1.Решить квадратное уравнение: х2-10х+26=0 2. Даны числа: 8i-3; 2-i Вычислить сумму, разность, произведение и частное этих чисел.
Вариант 12. 1.Решить квадратное уравнение: х2 +х+4,25=0 2. Даны числа: 5i-2; 3i+1 Вычислить сумму, разность, произведение и частное этих чисел.
Вариант13. 1.Решить квадратное уравнение: х2-х+4,25 =0 2. Даны числа: 17+31i; 7+i Вычислить сумму, разность, произведение и частное этих чисел.
Вариант 14. 1.Решить квадратное уравнение: х2-16х+20=0 2. Даны числа: 5-6i; -10+8i Вычислить сумму, разность, произведение и частное этих чисел.
Вариант 15. 1.Решить квадратное уравнение: х2+16х+20=0 2. Даны числа: 1+2i; 2-i Вычислить сумму, разность, произведение и частное этих чисел. Вариант16. 1.Решить квадратное уравнение: х2+8х+17=0 2. Даны числа: 5+3i; 2+i Вычислить сумму, разность, произведение и частное этих чисел.
Вариант 17. 1.Решить квадратное уравнение: х2-8х +17=0 2. Даны числа: 4-5i; -2+7i Вычислить сумму, разность, произведение и частное этих чисел.
Вариант 18. 1.Решить квадратное уравнение: х2 +4х +40=0 2. Даны числа: 3+4i; 6-8i Вычислить сумму, разность, произведение и частное этих чисел.
Вариант 19. 1.Решить квадратное уравнение: х2-4х+40=0 2. Даны числа:-4+6i; 3-2i Вычислить сумму, разность, произведение и частное этих чисел.
Вариант20. 1.Решить квадратное уравнение: х2+2х+50=0 2. Даны числа: 4-I; -2+i Вычислить сумму, разность, произведение и частное этих чисел. Вариант21. 1.Решить квадратное уравнение: х2 -2х +50=0 2. Даны числа: 1+2i; 1-9i Вычислить сумму, разность, произведение и частное этих чисел.
Вариант 22. 1.Решить квадратное уравнение: х2-6х+25=0 2. Даны числа: 5+2i; 8-6i Вычислить сумму, разность, произведение и частное этих чисел.
Вариант23. 1.Решить квадратное уравнение: х2+6х +25 =0 2. Даны числа: 1+2i; 2+i Вычислить сумму, разность, произведение и частное этих чисел.
Вариант 24. 1.Решить квадратное уравнение: х2 +8х+17 =0 2. Даны числа: 3+2i: 3-2i Вычислить сумму, разность, произведение и частное этих чисел.
Вариант 25. 1.Решить квадратное уравнение: х2 -8х+17=0 2. Даны числа: 7-24i; 4-3i Вычислить сумму, разность, произведение и частное этих чисел. Вариант 26. 1.Решить квадратное уравнение: Х2- 4х +20 =0 2. Даны числа: 6i-7; 3+4i Вычислить сумму, разность, произведение и частное этих чисел.
Вариант27. 1.Решить квадратное уравнение: х2+4х+29 =0 2. Даны числа: 3-5i; -2+9i Вычислить сумму, разность, произведение и частное этих чисел.
Вариант28. 1.Решить квадратное уравнение: х2 +2х+26=0 2. Даны числа: 1+13i: 3-4i Вычислить сумму, разность, произведение и частное этих чисел.
Вариант 29. 1.Решить квадратное уравнение: х2-4х+13=0 2. Даны числа: 8+2i; -3-4i Вычислить сумму, разность, произведение и частное этих чисел.
Вариант 30 1.Решить квадратное уравнение: х2 -6х+10 =0 2. Даны числа: 5-I; -3+7i Вычислить сумму, разность, произведение и частное этих чисел. Корни. Определение корня. Действительным корнем n-й степени из действительного числа а называется такое число х, что х= Математически определение корня можно записать так:
Неотрицательный корень n-й степени из неотрицательного числа называется арифметическим корнем. В элементарной математике выражение
Если а
2.2. Действия над корнями. Для арифметических корней справедливы следующие соотношения: - корень из произведения сомножителей равен произведению корней из этих сомножителей.
- корень из частного равен частному корней из делимого и делителя.
-подкоренное число можно возвести в любую степень, умножив на это же число показатель корня.
- если a и b положительные числа, то a Эта формула применяется как слева направо, так и справа налево. При использовании её нужно помнить, что для любых n она верна лишь при положительных a и d , а при нечётных n формула верна для любых действительных a и b . Например:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
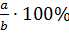
 .
.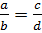
 d=b
d=b  ; d=
; d= 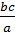
 ; c=
; c= 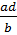

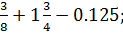
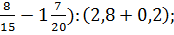
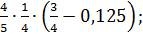
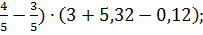
 ;
; ;
; ;
; ;
;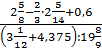 ;
; ;
; ;
; ;
; ;
;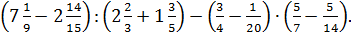
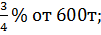
 ;
;
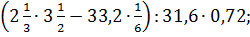
 ;
; .
. ;
; ;
; .
.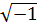 , так как не существует такого действительного числа, квадрат которого отрицателен. Петербургский математик Эйлер обозначил
, так как не существует такого действительного числа, квадрат которого отрицателен. Петербургский математик Эйлер обозначил  через i, тогда уравнение Х2+а2=0 имеет решения х =
через i, тогда уравнение Х2+а2=0 имеет решения х =  .
. .
. =
=  =
=  (1
(1  .
. +
+  i.
i. .
. = а.
= а. = 2; но
= 2; но  -2, хотя
-2, хотя  = 4;
= 4;  = -2.
= -2. , а числа m и n- натуральные, то
, а числа m и n- натуральные, то =
=  и
и  =
=  .
. …
… =
=  .
. .
. =
=  .
. =
=  .
.