
|
|
Формулы сокращённого умножения.Часто используются следующие формулы сокращённого умножения: 1) Квадрат суммы и квадрат разности (а+в)2 = а2+2ав+в2; (а-в)2 = а2-2ав+в2; 2) Разность квадратов а2-в2 = (а-в)(а+в); 3) Куб суммы и куб разности (а+в)3 = а3+3а2в+3ав2+а3; (а-в)3 = а3-3а2в+3ав2-а3; 4) Сумма кубов и разность кубов а3+в3=(а+в)(а2-ав+в2); а3-в3=(а-в)(а2+ав+в2). Примеры: 1. Упростить выражение: 1) 3(у-1)2+6у = 3(у2-2у+1)+6у=3у2-6у+1+6у=3у2+1 2) (2в-3)(3в+2)-3в(2в+3)=6в2+4в-9в-6-6в2-9в=-14в-6. Алгебраические дроби. Выражение вида Алгебраическая дробь удовлетворяет свойствам обыкновенной дроби, её можно сокращать и расширять, две дроби можно сравнивать, складывать, умножать и т.д. Примеры: 1. Сократить дробь:
2. Упростить выражение: а) б) в) г)
Задание 5. 1. Сократить дробь: 1) 2) 3) 4) 5) 2. Выполнить сложение или вычитание дробей: 1) 2) 3) 4) 5) 3. Умножение или деление дробей: 1) 2) 3) 4) 5) 4. Выполнить действия: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) 18) 19) 20) 21) 22) 23) 24) 25) 26) 27) 28) 29) 30)
Логарифм. Определение логарифма. Логарифмом числа b по данному основанию а называется показатель степени с, в которую нужно возвести основание а, чтобы получить число b. Обозначение:
Основное логарифмическое тождество:
Логарифм с основанием е=2,71828…, называется натуральным логарифмом и обозначается Логарифмирование действие, заключающееся в нахождении логарифма числового, алгебраического или иного выражения. Логарифмирование – одно из действий, обратных возведению в степень: если Действие, обратное логарифмированию, называется потенцированием. Этим действием по логарифму выражения восстанавливается само выражение.
Свойства логарифмов. Свойства логарифмов, используемые при выполнении различных преобразований и решении уравнений при а 1). 2). 3). 4). 5). 6). Формула перехода от логарифма по одному основанию к логарифму по другому основанию.
Множитель В частном случае при х = a Отношение логарифмов двух чисел, вычисленных при одинакоых основаниях, есть величина постоянная для данных чисел и независящая от выбора основания:
Примеры: 1). Прологарифмировать по основанию 2 выражение: Х =
2). Определить значение х, если:
Х= 3) Вычислить : а) б) в)
Задание 6. Вариант1. 1. Вычислить: а) б) в) 2. Прологарифмировать выражение: Х= 3. Найти х, если
Вариант 2. 1. Вычислить: а) б) в) 2. Прологарифмировать выражение: Х= 3. Найти х, если
Вариант 3. 1. Вычислить: а) б) в) 2. Прологарифмировать выражение: Х= 3. Найти х, если 4. Вариант 4. 1. Вычислить: а) б) в) 2. Прологарифмировать выражение: Х= 3. Найти х, если
Вариант 5. 1. Вычислить:
2. Прологарифмировать выражение: Х= 3. Найти х, если
Вариант6 1. Вычислить
2. Прологарифмировать выражение: Х= 3. Найти х, если
Вариант7 1. Вычислить: а) б) в) 2 2. Прологарифмировать выражение: х= 3. Найти х, если
Вариант 8 1. Вычислить:
2. Прологарифмировать выражение: Х= 3. Найти х, если
Вариант 9. 1. Вычислить: а) б) в) 2. Прологарифмировать выражение: Х=3 3. Найти х, если
Вариант 10. 1. Вычислить: а) б) в) 2. Прологарифмировать выражение: Х=4 3. Найти х, если
Вариант 11 1. Вычислить: а) б) в) 2. Прологарифмировать выражение: Х= 3. Найти х, если
Вариант 12. 1. Вычислить: а) б) в) 3 2. Прологарифмировать выражение: Х= 3. Найти х, если
Вариант 13. 1. Вычислить: а) б) в) 2. Прологарифмировать выражение: Х= 3. Найти х, если
Вариант 14. 1. Вычислить: а) б) в) 2. Прологарифмировать выражение: Х= 3. Найти х, если
Вариант 15. 1. Вычислить:
2. Прологарифмировать выражение:
3. Найти х, если
Вариант16. 1. Вычислить: а) б) в) 2. Прологарифмировать выражение: Х= 3. Найти х, если
Вариант17. 1. Вычислить: а) б) в) 2. Прологарифмировать выражение: Х= 3. Найти х, если
Вариант 18. 1. Вычислить: а) б) в) 2. Прологарифмировать выражение: Х= 3. Найти х, если
Вариант 19. 1. Вычислить: а) б) в) 2. Прологарифмировать выражение: Х=15 3. Найти х, если
Вариант 20. 1. Вычислить: а) б) в) 2. Прологарифмировать выражение:
3. Найти х, если
Вариант 21. 1. Вычислить: а) б) в) 2. Прологарифмировать выражение: Х= 3. Найти х, если
Вариант 21. 1. Вычислить: а) б) в) 2. Прологарифмировать выражение: 3. Найти х, если
Вариант 22. 1. Вычислить: а) б) в) 2. Прологарифмировать выражение:
3. Найти х, если
Вариант23. 1. Вычислить: а) б) в) 2. Прологарифмировать выражение:
3. Найти х, если
Вариант 24 1. Вычислить: а) б) в) 2. Прологарифмировать выражение:
3. Найти х, если
1. Вычислить: а) б) в) 2. Прологарифмировать выражение:
3. Найти х, если
Вариант 26 1. Вычислить: а) б) в) - 2. Прологарифмировать выражение:
3. Найти х, если 4. Вариант 27 1. Вычислить: а) б) в) 2. Прологарифмировать выражение:
3. Найти х, если
Вариант28 1. Вычислить: а) б) в) 2. Прологарифмировать выражение:
3. Найти х, если
Вариант 29 1. Вычислить: а) б) в) 2. Прологарифмировать выражение:
3. Найти х, если
Вариант 30 1. Вычислить: а) б) в) 2. Прологарифмировать выражение:
3. Найти х, если
Основы тригонометрии. Слово «тригонометрия» происходит от слияния греческих слов «треугольник» и «измеряю». Тригонометрия играет важную роль не только в математике, но и во многих других науках. С помощью тригонометрических функций описываются такие явления, как движение планет, циклические изменения в деятельности человека и животных, морские приливы и отливы, колебания маятника, электромагнитные явления в различных технических установках и т.д. Обилие формул в тригонометрии несколько затрудняет усвоение всего материала, поэтому требуется максимум усилий для успешного усвоения данной темы. 6.1. Радианная мера угла. Широко известны следующие единицы измерения углов: градус, минута, секунда. При решении задач механики, астрономии, электротехники широко применяется ещё одна единица измерения углов: так называемый радиан. Радианом называется центральный угол, опирающийся на дугу длина которой равна радиусу. 1рад.= Величина центрального угла не зависит от длины радиуса окружности. Установим связь между градусным и радианным измерениями углов: 360 Формула перехода от градусного измерения к радианному имеет вид: а =
Формула перехода от радианного измерения к градусному:
Длина дуги окружности равна радианной мере дуги, умноженной на радиус этой дуги: L = aR.
Примеры: 1) Чему равна радианная мера дуги 300 По формуле получим: а = 2) Чему равна градусная мера дуги По формуле получим:
6.2. Тригонометрические функции. Окружность с центром в начале координат и радиусом, равном 1, называется единичной окружностью. Точку А(1;0) единичной окружности примем за начало отсчёта дуг, а положительную полуось ОХ – за начальную сторону угла. Вращение единичного радиуса-вектора от положительной полуоси ОХ против движения часовой стрелки назовём положительным, а по часовой стрелки – отрицательным. Дуги первой четверти заключены в промежутке 0 Длина целой числовой единичной окружности равна
У М А(1;0) 0 х Абсцисса х точки М числовой единичной окружности называется косинусом числа Х= Ордината у точки М числовой единичной окружности называется синусом числа У= Отношение ординаты точки М к её абсциссе называется тангенсом числа
Отношение абсциссы точки М к её ординате называется котангенсом числа
В таблице приведены значения синуса, косинуса, тангенса и котангенса углов 0
Рассмотрим знаки тригонометрических функций: - и второй четвертях и отрицателен в третей и четвёртой четвертях; - так как и третей четвертях и отрицателен во второй и четвёртой четвертях; -так как tg положительны в первой и третей четвертях и отрицательны во второй и четвёртой четвертях. Знаки тригонометрических функций по четвертям приведены в таблице:
Из таблицы видно, что функция Поскольку 7.3. Основные тригонометрические тождества.
1+ Используя основные тригонометрические тождества, можно выразить через данную тригонометрическую функцию остальные функции. Пример: Дано:
6.4. Формулы приведения. Формулы приведения позволяют выразить тригонометрические функции углов При применении формул приведения рекомендуется пользоваться следующими правилами: 1. Если убирается целое число 2. Знак, с которым нужно брать функцию находится по знаку первоначальной функции. Пример: Вычислить
6.5.Формулы суммы и разности двух углов. Для нахождения тригонометрическихфункций суммы и разности двух аргументов применяются следующие формулы:
6.6. Формулы двойного угла.
6.7. Формулы половинного угла.
6.8.Преобразование суммы тригонометрических функций в произведение. Задание 7. 1. Вычислить выражения: 1) 2) 3) 4) 5) 6) 3tg930 7) 8) 2. Упростить: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 7.Функции. Функцией называется закон, по которому каждому значению величины х, называемой аргументом ставится в соответствие единственное число у. Множество значений х называется областью определения, а множество значений у – областью значений функции.
7.1Линейная функция. Линейная функция задаётся формулой: у = кх + в. График линейной функции – прямая. Число к называется угловым коэффициентом и равно тангенсу угла наклона прямой к оси абсцисс. Свойства линейной фукнкции: 1) Область определения: множество всех действительных чисел. 2) Область значений: множество всех действительных чисел при к 3) Чётность/нечётность: При к При к При к=0, в 4) Нули функции: у=0 при х = - 5) Промежутки знакопостоянства: При к При к 6) Промежутки монотонности: Про к
7.2. Квадратичная функция. Квадратичная функция имеет вид у=ах2+вх+с при а График квадратичной функции – парабола. Прямая х=- ув=- Свойства квадратичной функции: 1) Область определения: множество всех действительных чисел. 2) Область значений: при а 3) Чётность/нечётность функции: при в=0 функция чётная при в 4) Нули функции: корни квадратного уравнения. 5) Промежутки знакопостоянства: При а
При а При а 6) Промежутки монотонности: при а
7.3. Функция у = Обратной пропорциональностью называется функция, которую, можно задать формулой у = Областью определения этой функции является множество всех чисел, отличных от нуля. Областью значения функции является множество всех чисел, отличных от нуля, т.е. график функции не пересекает оси координат. При к
Задание 8. Построить график функции: 1) У= 2) У= 3) У= 4) У=- 5) У=х2-2х+3; 6) У=-х2+2х-4; 7) У=2х2+4х-2,5; 8) У=- 9) У=-2х2+4х-3; 10) У=2х2+4х+5; 11) У=-х2-4х; 12) У=-х2-2х; 13) У= 14) У= 15) У=- 16) У= 17) У= 18) У= 19) У= 20) У= 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
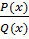 , где в числителе и знаменателе стоя многочлены, называется алгебраической дробью.
, где в числителе и знаменателе стоя многочлены, называется алгебраической дробью. =
=  =
= 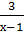 .
. =
=  =
= 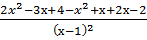 =
=  ;
; =
=  =
=  =
=  ;
; =
=  =
=  =
=  ;
; =
=  =
= 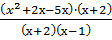 =
=  .
. ;
; ;
; ;
;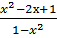 ;
; .
.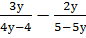 ;
; ;
; ;
; ;
; .
. ;
; ;
; ;
; ;
; .
.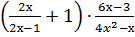 ;
; ;
; ;
; ;
; −
−  ;
;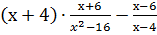 ;
; ;
; ;
; :
:  ;
; ;
; ;
; ;
;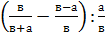 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; .
. = c. Предполагается, что b
= c. Предполагается, что b 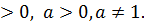
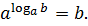
 десятичным логарифмом и обозначается lg x.
десятичным логарифмом и обозначается lg x. .
. , то a =
, то a = 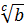 , c =
, c = 
 :
: ;
;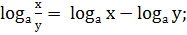
 = n
= n 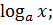
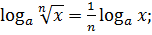
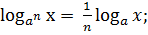
 .
. .
.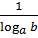 называется модулем перевода от системы логарифмов с основанием a к системе с основанием b.
называется модулем перевода от системы логарифмов с основанием a к системе с основанием b.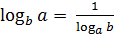 .
. , или
, или  .
.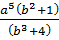
 = 5
= 5  .
. ;
;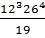 .
. =
=  ;
;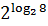 = 8;
= 8; =6
=6 ;
;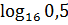 ;
; ;
; $
$ .
. ;
; ;
; ;
; ;
; .
. ;
; ;
; ;
; ;
;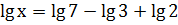 .
.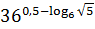 ;
;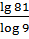 ;
; ;
; .
. ;
; ;
; ;
;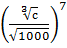
 .
. ;
; ;
; ;
; ;
;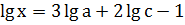 .
. ;
; ;
; ;
; ;
;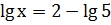 .
. ;
;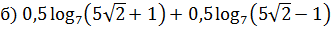 ;
; ;
;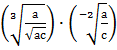 ;
;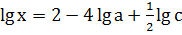 .
. ;
; ;
;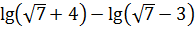
 ;
;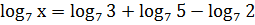 ;
; 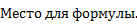
 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
;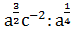
 .
. ;
;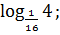
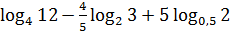 ;
;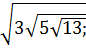
 .
. ;
;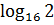
 ;
;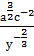
 .
. ;
;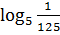 ;
; ;
; ;
; .
. ;
; ;
; ;
; ;
;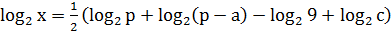 .
. ;
;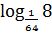 ;
; ;
; .
. .
.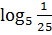 ;
; +
+ 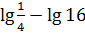
 ;
; .
.
 ;
;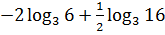
 ;
; .
.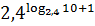
 ;
;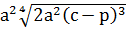 ;
; .
.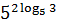
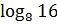 ;
; ;
; ;
; .
. ;
; ;
;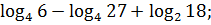
 ;
; ;
;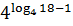
 ;
;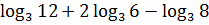
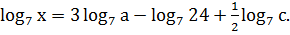
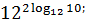
 ;
;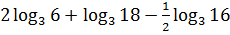
 .
.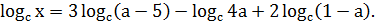
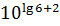
 ;
; ;
; ;
; .
. ;
; ;
; ;
; ;
;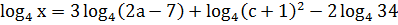 .
.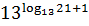 ;
; ;
; ;
; .
. ;
;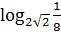 ;
;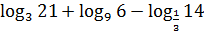 ;
;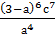 ;
; ;
;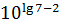 ;
; ;
; ;
; ;
; .
.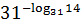 ;
; ;
; ;
; ;
; .
. ;
; ;
;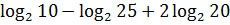 ;
; ;
;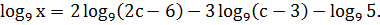
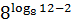 ;
; ;
; ;
; ;
; .
.
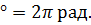
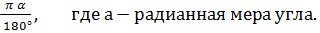
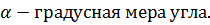
 .
.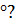
 =
=  .
.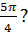
 =
=  =
=  .
. , второй четверти – в промежутке
, второй четверти – в промежутке 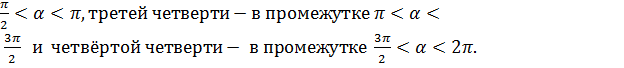
 Если два числа соответствуют одной и той же точке числовой единичной окружноти, то их разность кратна2
Если два числа соответствуют одной и той же точке числовой единичной окружноти, то их разность кратна2 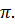
 .
.
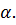
 .
. .
.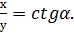
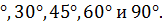 Прочерк сделан в том случае, когда выражение не имеет смысла.
Прочерк сделан в том случае, когда выражение не имеет смысла.





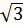
 положителен в первой
положителен в первой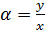 и ctg
и ctg  , то их знаки зависят от знаков х и у, поэтому tg
, то их знаки зависят от знаков х и у, поэтому tg 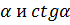



 1 и -1
1 и -1  то -1
то -1  , а функции tg
, а функции tg  не ограничены.
не ограничены. ;
; ;
; 1+
1+  =
=  ;
; ;
;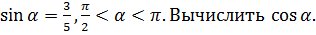
 ( перед радикалом стоит минус, так как во второй четверти
( перед радикалом стоит минус, так как во второй четверти  .
. угла
угла 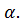
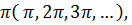 то функция названия не меняет, если убирается нецелое число
то функция названия не меняет, если убирается нецелое число  , то название функции меняется на сходное( синус - на косинус, тангенс – на котангенс и наоборот).
, то название функции меняется на сходное( синус - на косинус, тангенс – на котангенс и наоборот). =
=  .
.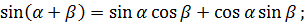

 ;
;
 ;
; .
. ;
; .
. ;
; 
 ;
; .
.  ;
; ;
; ;
; ;
; ;
;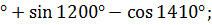
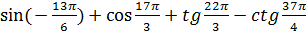 ;
;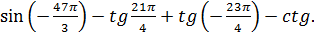
 ;
;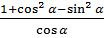 ;
; ;
;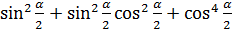 ;
; ;
; ;
;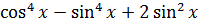 ;
; ;
; ;
; ;
; ;
;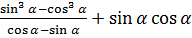 ;
; ;
; ;
;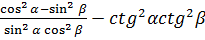 .
.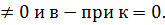
 функция общего вида;
функция общего вида;
 , в=0 функция нечётная;
, в=0 функция нечётная; функция чётная.
функция чётная. .
.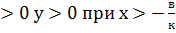 и у
и у  .
.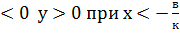 и у
и у  .
.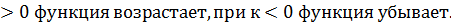
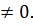
 является осью симметрии параболы. Вершина параболы имеет координаты хв=-
является осью симметрии параболы. Вершина параболы имеет координаты хв=-  . Число D=в2-4ас – дискриминант. Точки пересечения параболы с осью абсцисс являются корнями квадратного уравнения у=ах2+вх+с.
. Число D=в2-4ас – дискриминант. Точки пересечения параболы с осью абсцисс являются корнями квадратного уравнения у=ах2+вх+с. .
. , у
, у 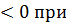
 .
.
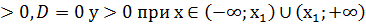 .
. при всех значениях х.
при всех значениях х.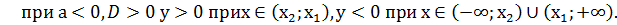
 .
.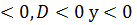 при всех значениях х.
при всех значениях х. функция возрастает на
функция возрастает на  ; при а
; при а 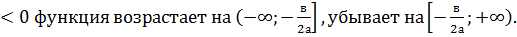

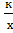 .
.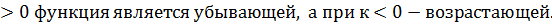
 ;
; ;
; ;
; ;
; ;
;
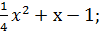
 ;
; ;
;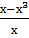 ;
; ;
;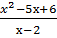 ;
; .
.