
|
|
Значение коэфициента В к формуле (4-156)
Таблица 4-8 Значения коэффициента
Таблица 4-9 Значения коэффициента сопротивления
Таблица 4-10 Значения коэффициента сопротивления ζ1-3 Для вытяжного тройника (рис. 4-39)
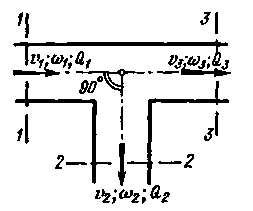
Таблица 4-11 Значения коэффициента сопротивления ζ1-2 для приточного тройника (рис. 4-40)
Таблица 4-12 Значения коэффициента сопротивления ζ1-3 для приточного тройника (рис. 4-40)
1Как видно, величина ζ1-3 (при Q1 = Q2), не совпадает с соответствующей величиной ζ1-3 в табл. 4-10. Это обстоятельство объясняется неточностью опытов. Таблица 4-13 Значения ζ3 Для простой задвижки, перекрывающей круглоцилиндрическую трубу (рис. 4-41)
Таблица 4-14 Значения ζ 3 для простой задвижки, перекрывающей трубу прямоугольного сечения (рис. 4-42)
5°. Тройник приточный (рис. 4-40); ω1 = ω2. Коэффициенты сопротивления ζ1-2 и
Рис. 4-39. Тройник вытяжной
где Коэффициенты сопротивления
где 60. Задвижки:
где v — скорость в трубе и h3 — потеря напора от сечения 1—1 до сечения 2—2 (см., например, рис. 4-41).
Рис. 4-40. Тройник приточный
Рис. 4-41. Задвижка простая на круглой трубе Величины а) для простой задвижки, перекрывающей трубу круглого поперечного сечения (рис. 4-41), из табл. 4-13 в зависимости от отношения a/D, где а —открытие задвижки; б) для простой задвижки, перекрывающей трубу прямоугольного поперечного сечения (рис. 4-42),— из табл. 4-14 в зависимости от отношения а/с, где с — высота трубы; в) для задвижки Лудло (рис. 4-43) на круглой трубе — из табл. 4-15 в зависимости от степени открытия a/D задвижки; г) для задвижки с симметричным сужением при полном ее открытии (рис. 4-44) — из табл. 4-16 в зависимости от диаметра трубы и других размеров задвижки, указанных на чертеже; д) для дискового (дроссельного) затвора (рис. 4-45), перекрывающего круглоцилиндрическую трубу, — из табл. 4-17 в зависимости от угла θ, показанного на чертеже; Таблица 4-15 Значения ζ3 для задвижки Лудло, перекрывающей круглоцилиидрическую трубу (рис. 4-43)
Таблица 4-16 Значения ζз для задвижки (при полном открытии) с симметричным сужением на круглоцилиидрической трубе (рис. 4-44)1
1 Значения ζ задвижки с симметричным сужением учитывают потери сужения и последующего расширения. Таблица 4-17 Значения ζз для дискового (дроссельного) затвора, перекрывающего круглоцилиидрическую трубу (рис. 4-45)
Таблица 4-18 Значения ζз для дискового (дроссельного) затвора, перекрывающего трубу прямоугольного поперечного сечения (рис. 4-45)
Таблица 4-19 Значения ζкл для захлопни клапана (рис. 4-46)
е) для дискового (дроссельного) затвора (рис. 4-45), перекрывающего трубу прямоугольного поперечного сечения, - из табл. 4-18 в зависимости от угла θ, показанного на чертеже. 7°. Клапаны:
где v — скорость в трубе и
Рис. 4-42. Задвижка простая на прямоугольной трубе
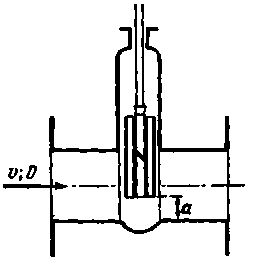
Рис.4-43. Задвижка Лудло
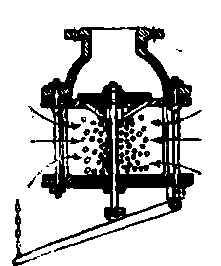
Рис. 4-44. Задвижка с сужением Величины а) для захлопки (рис. 4-46) — из табл. 4-19 в зависимости от углаθ,показанного на чертеже; б) для обратного клапана (рис. 4-47) — по табл. 4-20 в зависимости от диаметра трубы D; в) для всасывающего клапана с сеткой (рис. 4-48) — по табл. 4-21в зависимости от диаметра трубы.
Рис. 4-45 Дисковый затвор
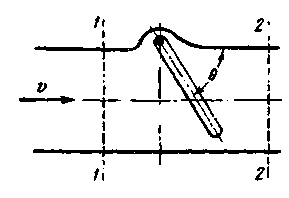
Рис. 4-46. Захлопка 8°. Решетки стержневые в трубе прямоугольного поперечного сечения (рис. 4-49) при .
Предполагается, что стержни решетки располагаются в продольных (по отношению к потоку) вертикальных плоскостях. Следует подчеркнуть, что приводимые в этом пункте данные широко используются и для подсчета потерь напора в случае безнапорного движения воды через решетку. Приводимые ниже данные заимствованы из [4-5]. 1. Чистая (незагрязненная) решетка. а) В случае
где v1 — средняя скорость перед решеткой; θ — угол наклона стержней решетки к горизонту;
Рис. 4-47. Обратный клапан
Рис. 4-48. Всасывающий клапан с сеткой
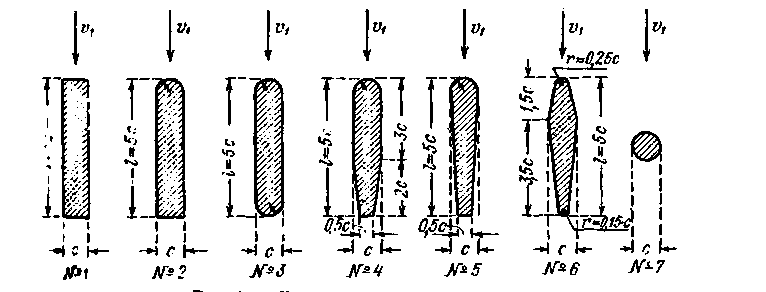
Рис. 4-49. Решётка стержневая а-ширина просвета между стержнями; с - толщина стержня; l-больший размер поперечного сечения стержня решетки (см. рис. 4-50);β1 — коэффициент, принимаемый по табл. 4-22 в зависимости от формы поперечного сечения стержней решетки
Рис. 4-50. Типы стержней (к рис. 4-49)
Таблица 4-20 Значения ζкл для обратного клапана (рис. 4-47)
Таблица 4-21 Значения ζкл для всасывающего клапана с сеткой (рис. 4-48)
Таблица 4-22 Значения коэффициента β1 формуле (4-159)
Таблица 4-23 Значения коэффициента β2 к формуле (4-160)
Таблица 4-24 Значения коэффициента ζ′ к формуле (4-160)
(различные формы этих сечений за соответствующими номерами показаны на рис. 4-50). б) В случае отношений 1/с и а/с любой величины
где θ — угол наклона стержней к горизонту; коэффициент β2 берется из табл. 4-23 в зависимости от формы поперечного сечения стержней; коэффициент
где ω' — площадь одного отверстия решетки; 2. Загрязненная решетка (в случае гидротехнического сооружения):
где а) при машинной очистке решетки х′ = 1,1÷1,3; б) при ручной очистке решетки х' = 1,5 ÷ 2,0. 3.Решетка (гидротехнического сооружения) с дополнительным каркасом, состоящим из добавочных горизонтальных стержней:
где коэффициент х" определяется по формуле
где L— высота решетки в свету (рис. 4-49); А — суммарная высота поперечных элементов:
где n1 - количество распорно-связных горизонтальных элементов (высотой d); n2 — количество промежуточных опорных балок (высотой z). 9°. Часто встречающиеся значения коэффициентов местного сопротивления ζj Таблица 4-25
Примечания к таблице. 1. О выходе трубы см. формулы (4-135) —(4-136). 2. Коэффи-Иенты местного сопротивления, рекомендуемые в табл. 4-25, относятся к формуле
где v2 – средняя скорость за местным сопротивлением. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 к формуле (4-157)
к формуле (4-157) 0
0


 учитывающие снижение напора (hj )1-2 от сечения 1 — 1 до сечения 2 — 2
учитывающие снижение напора (hj )1-2 от сечения 1 — 1 до сечения 2 — 2

 находится по табл. 4-11 в зависимости от отношений
находится по табл. 4-11 в зависимости от отношений  и
и  (обозначения указаны на чертеже).
(обозначения указаны на чертеже). и
и  учитывающие снижение напора (hj )1-3 от сечения 1 — 1 до сечения 3—3 (рис. 4-40):
учитывающие снижение напора (hj )1-3 от сечения 1 — 1 до сечения 3—3 (рис. 4-40):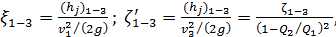
 находится по табл. 4-12 в зависимости от отношения
находится по табл. 4-12 в зависимости от отношения  .
. ,
,
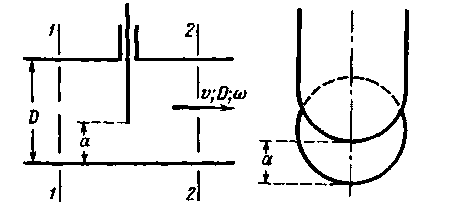
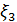 берутся:
берутся: ,
, — потери напора в клапане.
— потери напора в клапане.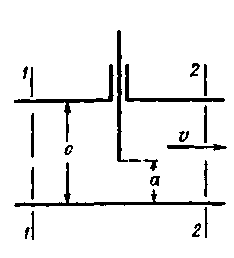

 берутся:
берутся: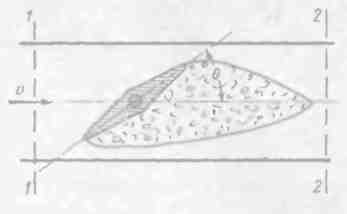
 (4-158)
(4-158) = 5;
= 5;  > 1,0; величина
> 1,0; величина  определяется по формуле Кришмера[46]
определяется по формуле Кришмера[46]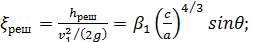 (4-159′)
(4-159′)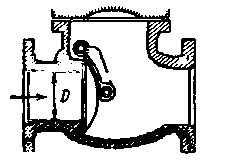


 (4-159′′)
(4-159′′) — из табл. 4-24 в зависимости от отношения ω2/ω1и отношения l/d'; здесь ω1— площадь живого сечения перед решеткой; ω2 — полная площадь решетки в свету; d' — величина, равная:
— из табл. 4-24 в зависимости от отношения ω2/ω1и отношения l/d'; здесь ω1— площадь живого сечения перед решеткой; ω2 — полная площадь решетки в свету; d' — величина, равная: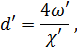
 — смоченный периметр этого отверстия.
— смоченный периметр этого отверстия.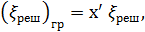
 определяется, как указано выше (в п. 1); численное значение коэффициента х' принимается равным:
определяется, как указано выше (в п. 1); численное значение коэффициента х' принимается равным: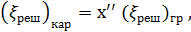

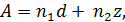


 (4-160)
(4-160)