
|
|
ОСТАЛЬНЫЕ СЛУЧАИ МЕСТНЫХ ПОТЕРЬ НАПОРА. ОБЩАЯ ФОРМУЛА ВЕЙСБАХА
На рис. 4-36 для примера показаны два случая местных потерь напора (местных сопротивлений): задвижка и поворот трубы. Эти случаи и им подобные, так же как и сужения трубы (см. § 4-17), характеризуются наличием струи и водоворотных областей А. Как было указано выше, потеря напора hj главным образом сосредоточивается только на участке струи за сжатым сечением, где имеется расширение струи. Поэтому hj в любом случае можно было бы определить в соответствии с формулой Борда, переписав ее так:
где
Рис. 4-34. Протекание жидкости при наличии задвижки З(а) и при наличии поворота трубы (б) Согласно (4-134),
причем здесь со — живое сечение транзитной струи, заполняющей всю трубу; ωс - живое сечение транзитной струи по линий сжатого сечения С — С. Однако практически ζj по (4-155) в общем случае найти затруднительно, так как нам неизвестна площадь ωс. Учитывая вместе с тем приведенные соображения, Вейсбах предложил вычислять любую местную потерю напора по формуле (4-154), считая, что коэффициент местного сопротивления, входящий в эту формулу, в общем случае должен определяться экспериментальным путем для различных встречающихся в практике местных сопротивлений. Экспериментальные значения ζj приводятся в справочной литературе. Некоторые сокращенные данные по этому вопросу даются ниже (стр. 194-203). Величина ζj зависит от того, какую скорость будем подставлять в формулу Вейсбаха (4-154): относящуюся к сечению, взятому до местного сопротивления, или за ним. Из формулы (4-154) ясно, что величина hj прямо пропорциональна скоростному напору. Практически во всех случаях hj определяется по формуле (4-154), в которой ζj — эмпирический коэффициент пропорциональности; только в двух случаях (при резком расширении и наиболее резком сужении) этот коэффициент устанавливается теоретическим путем — путем совместного решения уравнений Бернулли и количества движения. Надо, впрочем, отметить следующее. Кирхгоф, Н. Е. Жуковский и другие дали особые методы для определения размера «сжатого» сечения при истечении жидкости из различных отверстий. Эти методы основаны на теории функций комплексной переменной и относятся к плоскому безвихревому установившемуся движению идеальной невесомой жидкости. Приближенное (а в некоторых случаях и точное) использование указанных методов для определения площади ωс сжатого сечения несколько расширяет круг задач, для которых ζj может быть найдено теоретически. В случае квадратичной области сопротивления, которую, мы имели в виду выше, величина ζj не должна зависеть от числа Рейнольдса, а следовательно, не должна зависеть: от скорости v, от рода жидкости (т. е. от величины v), а также от размеров узла, где возникает данная местная потеря напора. Величина X,t должна зависеть практически только от геометрической формы упомянутого узла. Заметим, что в случае доквадратичной области сопротивления или в случае ламинарного режима движения жидкости в трубах (этих случаев мы выше вовсе не касались) величина ζj- оказывается зависящей от числа Рейнольдса, а следовательно, от величин v и v и размеров потока (а также, разумеется, и от геометрической формы рассматриваемого узла). В связи с этим расчеты местных потерь в указанных случаях получаются более сложными. В заключение подчеркнем, что приведенные выше значения ζj относятся к условиям, когда расстояния между узлами, для которых определяются hj, достаточно велики, т. е. такие, что один узел практически не влияет на кинематическую картину движения жидкости в пределах другого узла.
СОКРАЩЕННЫЕ СПРАВОЧНЫЕ ДАННЫЕ О ВЕЛИЧИНЕ КОЭФФИЦИЕНТА МЕСТНОГО СОПРОТИВЛЕНИЯ Х,} (В СЛУЧАЕ УСТАНОВИВШЕГОСЯ НАПОРНОГО ТУРБУЛЕНТНОГО ДВИЖЕНИЯ ЖИДКОСТИ)
Выше были рассмотрены следующие случаи местных потерь напора hj: 1) резкое расширение трубы (см. стр. 183); 2) выход из трубы (см. стр. 187); 3) постепенное расширение трубы (см. стр. 188); 4) сужение трубопровода и вход в трубопровод (см. стр. 190). Далее приводятся эмпирические данные,[44] служащие для определения коэффициента местного сопротивления ζj, входящего в формулу Вейсбаха (4-154) и относящегося к другим местным потерям. Общее обозначение коэффициента ζj, далее заменяется частными его обозначениями: ζд (коэффициент, относящийся к диафрагме), ζ р.пов (коэффициент, относящийся к резкому повороту трубы) и т. д. 1°. Диафрагма с острыми краями в трубе круглого поперечного сечения при
где v2 — средняя скорость в круглом отверстии диафрагмы площадью ω2. Величина ζд берется из табл. 4-5 в зависимости от отношений ω2/ω1, и ω2/ω3 (обозначения ω1 и ω3 см. на чертеже). 2°. Резкий поворот трубы иа угол θ; рис. 4-38, а:
где величина коэффициента сопротивления резкого поворота
причем здесь эмпирические коэффициенты А и В берутся (согласно И. Е. Идельчику) из табл. 4-6 и 4-7.
Рис. 4-37. Диафрагма 3°. Плавный поворот трубы на угол θ(при ReD≥2∙105); рис. 4-38,б:
где величина коэффициента сопротивления плавного поворота
причем здесь 4°. Тройник вытяжной (рис. 4-39); ω1 = ω2. Коэффициенты сопротивления ζ2-3 и ζ′2-3. учитывающие снижение[45] (изменение) напора (h)2-3 от сечения 2 - 2 до сечения 3-3;
где
Рис. 4-38. Поворот трубы Коэффициенты сопротивления
где Таблица 4-5 Значения коэффициента сопротивления
Таблица 4-6 Значения коэффициента А к формуле (4-156)
Таблица 4-7 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
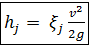 (4-154)
(4-154) можно назвать коэффициентом местного сопротивления.
можно назвать коэффициентом местного сопротивления.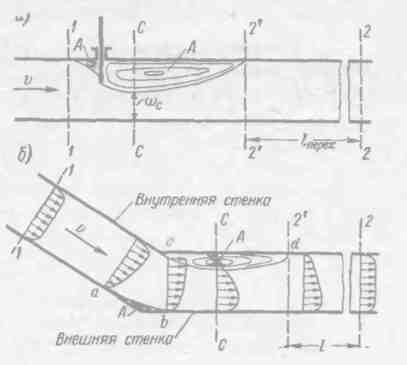
 (4-155)
(4-155) и при
и при  (рис. 4-37):
(рис. 4-37): ,
, ,
, для гладких труб круглого и квадратного поперечного сечения вычисляется по формуле
для гладких труб круглого и квадратного поперечного сечения вычисляется по формуле , (4-156)
, (4-156)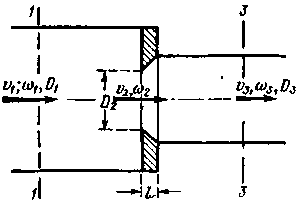
 ,
, (4-157)
(4-157) берется из табл. 4-8, составленной по данным Вейсбаха.
берется из табл. 4-8, составленной по данным Вейсбаха.
 находится по табл. 4-9 в зависимости от отношений ω2/ω3 и Q2/Q3 (обозначения указаны на чертеже)
находится по табл. 4-9 в зависимости от отношений ω2/ω3 и Q2/Q3 (обозначения указаны на чертеже)
 и
и  , учитывающие снижение напора
, учитывающие снижение напора  от сечения 1 -1 до сечения 3 — 3 (рис. 4-39)
от сечения 1 -1 до сечения 3 — 3 (рис. 4-39)
 .
. диафрагмы с острыми краями
диафрагмы с острыми краями ,
,
