|
|
РАСПРЕДЕЛЕНИЕ ОСРЕДНЕННЫХ СКОРОСТЕЙПО ЖИВОМУ СЕЧЕНИЮ ПОТОКА ПРИ ТУРБУЛЕНТНОМ ВЯЗКИЙ ПОДСЛОЙ. ГЛАДКИЕ И ШЕРОХОВАТЫЕ ТРУБЫ. ПОГРАНИЧНЫЙ СЛОЙ 1°. Общий характер распределения осредненных скоростей по живому сечению потока при турбулентном движении. Вязкий подслой.Представим на рис. 4-15 эпюру осредненных скоростей для живого сечения АВ. Как показывает опыт, эта эпюра характеризуется следующим:
Рис. 4-15. Эпюра скоростей (осредненных) при турбулентном движении; 𝛿 — толщина вязкого подслоя
1) вблизи стенок скорость u вдоль линии ВА резко увеличивается, т. е. в этом месте 2) на некотором удалении от стенки и изменяется относительно мало; При помощи подкрашивания движущейся жидкости можно убедиться в том, что жидкость из центральной части потока переносится к боковым границам потока; наоборот, жидкость от границ потока (с низшим содержанием кинетической энергии) переносится к центру потока. Именно в результате такого турбулентного перемешивания распределение скоростей по живому сечению в средней части потока оказывается при турбулентном движении значительно более равномерным, чем при ламинарном. Если в случае ламинарного напорного движения в круглой трубе Согласно исследованиям Л. Прандтля в турбулентном потоке скорость движения жидких частиц непосредственно у стенки равна нулю. В соответствии с этим принято считать, что вблизи стенок русла имеется тонкий слой жидкости толщиной 𝛿, где скорости столь малы, что в пределах этого слоя получается движение жидкости, близкое к ламинарному. Этот слой называется вязким (иногда «ламинарным») подслоем. Толщина его мала
Рис. 4-16. Гладкие (а) и шероховатые (б) русла
(составляет, например, сотые или тысячные доли глубины потока или диаметра трубопровода; на рис. 4-15 толщина ламинарного подслоя преувеличена — показана не в масштабе). Между так называемым турбулентным ядром потока и вязким подслоем имеется тонкий переходной участок, в пределах которого пульсации скоростей резко снижаются. 2°. Гидравлически гладкие и шероховатые трубы. На рис. 4-16 обозначены: Δ - высота выступов шероховатости стенки русла и 𝛿 — толщина вязкого подслоя. При наличии схемы а выступы шероховатости покрываются (сглаживаются) вязким подслоем (𝛿 > Δ), причем получаем так называемые гладкие стенки (иногда говорят «гидравлически гладкие» стенки). В этом случае потери напора по длине оказываются не зависящими от шероховатости стенок русла. При наличии схемы б выступы шероховатости не покрываются полностью вязким подслоем (𝛿 < Δ); эти выступы «вклиниваются» (как отдельные «бугорки») в турбулентную зону, и о них могут «ударяться» жидкие частицы турбулентного ядра потока[19]. В этом случае потери напора по длине Особыми исследованиями было установлено, что толщина вязкого подслоя 𝛿 уменьшается с увеличением числа Рейнольдса. Отсюда ясно, что понятия гладкой и шероховатой стенок являются понятиями относительными: одна и та же стенка в одних условиях (при малых Re) может быть «гладкой», в других же условиях (при больших Re) может быть «шероховатой». 3°. Зависимости для построения эпюры осредненных скоростей в случае напорных круглых труб при турбулентном движении. Вопросу о распределении осредненных скоростей по живому сечению турбулентного потока посвящено большое количество теоретических и экспериментальных работ. Рассмотрим для примера круглоцилиндрическую трубу (см. рис. 4-6). Для того чтобы получить уравнение кривой АСВ, ограничивающей эпюру осредненных продольных скоростей, выписываем, как и в случае ламинарного движения (см. § 4-4), два разных выражения для касательного напряжения (см. продольный центральный «жидкий столб» на рис. 4-6): 1) уравнение равномерного движения (4-18) в виде
2) уравнение для турбулентного касательного напряжения (4-55)
Решая эту систему уравнений, так же как и в случае ламинарного движения, получаем [см. уравнение (4-31)]
Интегрируя это уравнение, имеем
где В случае ламинарного движения, получив выражение, аналогичное (4-61), имели возможность вынести за интеграл величину η (как величину постоянную для данной жидкости). При этом уравнение (4-61) легко решалось. В случае турбулентного движения величина Зависимость Прандтля для гладких труб после введения в нее некоторых эмпирических коэффициентов, найденных И. Никурадзе, имеет вид:
где определяется скорость u; Величину
откуда
где гидравлический радиус R = D/4. Полученные для круглоцилиндрических напорных труб полуэмпирические уравнения кривой ABC (рис. 4-17) не лишены некоторых недостатков; они не всегда удовлетворяют пограничным условиям: при r=r0 иногда дают скорость (непосредственно на стенке — в самой близи стенки, где имеется ламинарный подслой) u = -∞; по зависимости Прандтля величина градиента скорости действительности. Вместе с тем эти формулы дают достаточно хорошее совпадение с опытами для основной части ядра потока.
Рис. 4-17. Распределение осреднённых скоростей в круглой трубе при турбулентном движении
Рис. 4-18. Экспериментальный график для величины m в формуле (4-64)
Практически более удобными являются приближенные формулы, выражающие закон распределения скоростей в виде степенных функций. Карман (в 1921 г.) на основании теоретических исследований предложил записывать этот закон для гладких труб в виде:[20]
где А. Д. Альтшуль в 1956 г. показал, что зависимость (4-64) действительна не только для гладких, но и для шероховатых труб (т. е. для всей области турбулентного движения), если величину показателя
4°. Пристенный пограничный слой. Покажем на рис. 4-19 неподвижную горизонтальную пластинку АВ достаточной длины. Далее, рассматривая плоскую задачу, будем считать, что на эту пластинку слева «набегает» горизонтальный поток реальной жидкости, причем эпюра скоростей, построенная для этого потока в вертикальном его сечении О — О (см. рисунок) характеризуется величинами u = const по всей высоте сечения О — О.
Рис. 4-19. Пристенные пограничные слои толщиной z0 (возникающие у неподвижной пластинки АВ; см. верхнюю и нижнюю области CAB)
Очевидно, реальная жидкость, набегая на пластинку АВ, получает, например, на верхней поверхности этой пластинки[22] касательные напряжения трения Рассматривая некоторое вертикальное сечение, например, сечение III-III, видим, что в связи с упомянутым подтормаживающим действием пластинки АВ, эпюра скоростей u в данном сечении будет ограничена кривой abed[23]. При этом в пределах участка высотой
Аналогичная картина будет и в других вертикальных сечениях, например, в сечениях I-I и II-II (см. рисунок). Однако величины
В связи со сказанным, можно наметить некоторую линию АС, выделяющую у стенки слой жидкости, характеризуемый следующим: 1)высота (толщина) этого слоя z0 по течению увеличивается; 2) в пределах его величины
Рис. 4-20. Развитие пристенного пограничного слоя в начале канала
3) за пределами его величины du/dn и τ изменяются (в соответствующих вертикальных сечениях) пренебрежимо мало, и следовательно, за указанными пределами вязкость жидкости можно не учитывать и считать жидкость как бы идеальной,[24] а движение жидкости потенциальным. Условимся пристенный слой, характеризуемый тремя отмеченными обстоятельствами, называть «пристенным пограничным слоем».
Рис. 4-21. Развитие пристенного пограничного слоя на начальном участке круглой напорной трубы (пограничный слой показан штриховкой); правее вертикали А2-А2, пограничный слой отсутствует
На рис. 4-20, заимствованном из [4-9], дана схема поступления жидкости из большого водоема в канал. На этой схеме показаны: ламинарная часть А пограничного слоя, турбулентная часть Б1 пограничного слоя и, наконец, область В, характеризуемая столь малыми значениями du/dn, что величиной трения в этой области можно пренебречь. Зону В можем рассматривать как область идеальной жидкости и считать, что в ней имеется потенциальное безвихревое движение (см. § 3-4 и 3-5). Трактуя понятие пристенного пограничного слоя несколько иначе, чем то было пояснено нами выше, автор данной схемы область Б2 называет «вполне развитым пограничным слоем»» (хотя эта область не удовлетворяет 1-му и 3-му условиям, отмеченным выше). 5°. Развитие пограничного слоя в напорной трубе. «Начальный участок» потока.Если на рис. 4-21 представить поступление реальной жидкости из какого-либо сосуда в круглую трубу, имеющую весьма плавный вход, то в начальном состоянии А1А1 трубы будем иметь почти равномерную эпюру скоростей и. Далее на длине l1 (до сечения А2А2) благодаря подтормаживающему действию напряжений трения τ0 (действующих со стороны стенок трубы на жидкость) толщина z0 пограничного слоя начинает увеличиваться по длине грубы (см. рисунок, на котором штриховкой показан пограничный слой, развивающийся в круглой трубе). В сечении А2А2 происходит «смыкание» рассматриваемого пограничного слоя (в точке b). Между верхней и нижней частями пограничного слоя на длине l1 показана незаштрихованная область a1 — b — а2; внутри этой области имеем потенциальное движение жидкости: в любом вертикальном сечении этой области скорости и = const (однако, по течению эти скорости увеличиваются).
Рис. 4-22. Эпюры скоростей в конце начального участка: а — ламинарный режим, б —турбулентный режим
Рассматривая рис. 4-21, следует различать помимо участка, где располагается пограничный слой, еще участок потока длиной l2 (между сечениями А2А2 и А3А3). В пределах этого участка происходит: а) переформирование эпюры скоростей и, получившейся в сечении А2А2, в эпюру скоростей (показанную в сечении А3А3), свойственную равномерному движению; б) изменение уровня пульсации скоростей до уровня, свойственного равномерному движению. «Начальным участком» трубопровода следует называть участок длиной Выше мы говорили о турбулентном движении; надо учитывать, что аналогичный участок («начальный участок») должен иметь место и при ламинарном режиме. Длина начального участка ln для круглых труб (согласно экспериментальным данным) может быть принята (для турбулентного движения)
На рис. 4-22 представлены эпюры, сформировавшиеся в конце начальною участка (в сечении А3А3) при ламинарном и при турбулентном движении. Как видно, максимальная толщина пограничного пристенного слоя в напорной круглой трубе (имеющая место в сечении А3А3) равна половине диаметра трубы.
В. ПОТЕРЯ НАПОРА ПО ДЛИНЕ ПРИ ТУРБУЛЕНТНОМ § 4-9. ФОРМУЛА ВЕЙСБАХА - ДАРСИ КОЭФФИЦИЕНТ
Как показывают опыты, величина
где λ/4 — некоторый эмпирический коэффициент пропорциональности. Сопоставляя (4-67) с (4-15), можем написать:
откуда, учтя, что J = hl:l, получаем следующую общую зависимость для потерь напора по длине при равномерном установившемся движении:
где l — длина потока; R — гидравлический радиус. Для круглых напорных труб D = 4R, и потому для этих труб общая зависимость (4-69) переписывается в виде:
Формула (4-70) называется формулой Вейсбаха — Дарcи. Безразмерный коэффициент λ, входящий в нее, будем именовать коэффициентом гидравлического трения. В случае ламинарного напорного движения жидкости в круглой трубе мы уже получили выше теоретическую формулу (4-46) для λ. При турбулентном течении λ находится по эмпирическим формулам. Ранее считали, что коэффициент λ, входящий в выражение (4-70), является постоянной величиной; несколько позже его ставили в зависимость от средней скорости v или диаметра D. Некоторые авторы связывали величину λ только с шероховатостью стенок труб. Такого рода зависимости в настоящее время считаются устаревшими и неприемлемыми в практике. Современные расчетные формулы для λ предусматривают зависимость этого коэффициента в общем случае только от шероховатости стенок русла и от числа Рейнольдса. Величину λ в случае круглых труб можно найти для турбулентного движения (так же как и для ламинарного движения; см. выше), зная закон распределения скоростей по живому сечению. Действительно, формулу (4-70) можно переписать в виде
и затем, учтя (4-63), в виде
откуда
Выражение для Л. Прандтль в 1932 г. для гладких труб получил следующую формулу (исходя из некоторой неполной воображаемой модели):
Блазиус в 1913 г. на основании обработки многочисленных опытов по исследованию движения жидкости в круглых гладких (латунных) трубах при числах Рейнольдса ReD от 4000 до 100000 установил эмпирическую зависимость
Формулы для
§ 4-10. ИССЛЕДОВАНИЯ И. НИКУРАДЗЕ. ОБОБЩЕНИЕ ВОПРОСА О ПОТЕРЯХ НАПОРА Представим на рис. 4-23 трубу диаметром D с задвижкой К и двумя пьезометрами П. При помощи задвижки К можно изменять скорость v в трубе, причем для каждой такой скорости, установившейся в трубе, можно по пьезометрам определять (в случае установившегося движения) потерю напора
Рис. 4-23. Схема опытов Никурадзе Коэффициент гидравлического трения λ. согласно формулам (4-70) и (3-135), можно выразить через ReD:
причем по этой формуле, определив а опытов величины Проводя подобные опыты, И. Никурадзе исследовал (в 1933 г.) запорные круглоцилиндрические трубы, имеющие однозернистую равномерно распределенную искусственную шероховатость, которую он создавал, наклеивая на стенки трубы песчинки одинаковой высоты Δ на одинаковом расстоянии друг от друга. Результаты своих опытов Никурадзе представил в виде особого графика, по осям которого он отложил безразмерные величины λ и ReD, причем на таком графике был нанесен ряд кривых, вычисленных в соответствии с приведенной выше зависимостью; каждая кривая отвечала определенной так называемой относительной шероховатости:
где Δ можно назвать «высотой выступов шероховатости» (будем считать, что размер Δ весьма мал сравнительно с диаметром D). Этот график (см. далее рис. 4-24) позволил в удобной форме обобщить вопрос о потерях напора (в случае равномерного установившегося движения несжимаемой жидкости в круглой трубе) и наглядно показать следующее: 1) коэффициент λ, входящий в формулы (4-69) и (4-70), в самом общем случае зависит только от 2) имеются частные случаи движения жидкости, когда λ зависит или только от 3) имеются вполне определенные зоны сочетания λ и ReD, для которых в формулах, выражающих пропорциональность (::)
показатель степени m приобретает вполне определенное значение (равное единице, двум и т.п.). На рис. 4-24 показана схема графика Никурадзе. Пользуясь ею, поясним основные положения, вытекающие из рассмотрения данного графика, на котором показаны две «опорные» прямые: прямая I, построенная по уравнению (4-46) (см. линию 1 - 2 - 3); эта прямая называется прямой ламинарного режима; прямая II, построенная исходя из уравнения Блазиуса (4-75); назовем ее прямой Блазиуса.
Рис. 4-24. Схема графика Никурадзе (кривые λ =f(ReD) для различных
Откладывая в соответствующем масштабе по осям графика величины lgReD (по горизонтальной) и lgλ, (по вертикальной), мы на шкалах осей выписываем сами числа ReD и λ (а не величины их логарифмов). Построение графика в таких логарифмических координатах позволяет «опорные» линии I и II, выражаемые степенными функциями, представить в виде прямых. Все поле графика можно разбить на три зоны: Первая зона - зона ламинарного режима; она представлена отрезком прямой 1-2, построенной по уравнению (4-46). Здесь экспериментальные кривые Для этой зоны имеем следующее: а) величины ReD относительно малы, менее (ReD)K = 1000 ÷ 2300 [см. формулу (3-136)]; б) потеря напора λ = f(ReD), построенные для разных в одну прямую 1 - 2; в) потери напора прямо пропорциональны первой степени скорости [как то следует из формул (4-45) и (4-46); в данном случае показатель степени m = 1]; г) величина λ определяется формулой (4-46). Вторая зона - зона, расположенная между вертикалями III и IV (заштрихована), является зоной неустойчивого режима (см. § 3-24; зону (3) на рис. 3-42). Ее называют, как было отмечено выше, неустойчивой или переходной зоной (зоной, внутри которой происходит переход ламинарного режима в турбулентный и наоборот - турбулентного режима в ламинарный). Здесь: а) числа Рейнольдса лежат в пределах от 1000 ÷ 2300 до 4000 ÷ 40000; б) при движении жидкости по трубе на отдельных участках возникают отдельные области турбулентного режима, которые разрастаются, а затем исчезают и снова появляются. В связи с этим данная зона иногда называется зоной перемежающейся турбулентности. Заметим, что когда турбулентные области в трубе разрастаются, растет и сопротивление движению жидкости (в связи с ростом турбулентных касательных напряжений трения), при этом скорость Дополнительно надо иметь в виду еще следующее обстоятельство, которое может затруднять определение потерь напора (и, следовательно, величин λ) для области неустойчивого режима. Можно допустить, что при Q = const (а следовательно, и при Третья зона - зона турбулентного режима; эта зона располагается правее вертикали IV, отвечающей ReD ≈ 4000 ÷ 40000. Данная зона в свою очередь разбивается на три области. Первая область - «область гладких русел»; она представлена: а) при числах Рейнольдса ReD < 100000 - прямой линией II и б) при числах Рейнольдса ReD > 100000 - кривой линией, являющейся продолжением прямой II; данная кривая, начинающаяся от точки 4, на. рис. 4-24 не показана (она будет представлена далее на рис. 4-25 в виде самой нижней кривой линии). Для первой области имеем: a) б) h, не зависит от шероховатости, поскольку все кривые Δr= const сливаются в одну линию (здесь мы получаем гладкие трубы; выступы шероховатости покрыты ламинарным подслоем); в) ht а также X, зависит только от числа Рейнольдса, согласно формуле Блазиуса (4-75) или Прандтля (4-74),
Вторая область — «область доквадратичного сопротивления шероховатых русел», эта область лежит между прямой II и линией АВ.
Согласно Никурадзе, кривые Δr = const в этой области имеют вид, показанный сплошными линиями; согласно опытам ряда других авторов, эти кривые имеют другой вид (см. штриховые линии). Такое расхождение объясняют различием геометрических форм шероховатости, имевшей место при проведении опытов. Считают, что кривые Никурадзе относятся к однозернистой равномерно распределенной шероховатости; штриховые же кривые — к шероховатости разнозернистой, свойственной, например, стальным и чугунным трубам. Из сказанного выше ясно, что на левой границе рассматриваемой области кривые графика, опускаясь вниз, характеризуются в месте отрыва их от опорной прямой II показателем степени т, входящим в формулу (4-77), равным 1,75 На правой границе АВ области, где кривые графика переходят в горизонтальные прямые, m = 2,0 (см. ниже). Можно показать, что поднимающиеся кверху сплошные линии Никурадзе (расположенные внутри рассматриваемой области), характеризуются показателем степени т > 2,0. Отсюда заключаем, что т в пределах данной области изменяется от 1,75 до 2,0, причем для однозернистой равномерно распределенной шероховатости этот показатель, согласно Никурадзе, в промежутке между т = 1,75 и т = 2,0 должен иметь максимум (тмакс > 2,0); для разнозернистой же шероховатости, по данным других авторов, показатель т в пределах данной области монотонно возрастает от 1,75 до 2,0. Из графика видно, что для данной области λ, а также hl зависят как от числа Рейнольдса, так и от относительной шероховатости:
Третья область — «область квадратичного сопротивления шероховатых русел»; эта область располагается правее линии АВ. Здесь: а) потеря напора прямо пропорциональна квадрату скорости v (т = 2,0); б) коэффициент X не зависит от числа Рейнольдса ReD (все линии в) hl и λ зависят от относительной шероховатости:
В заключение необходимо отметить, что общий качественный характер связей, полученный Никурадзе для круглоцилиндрических напорных труб, разумеется, можно распространить и на потоки другого вида (напорные и безнапорные). Важно подчеркнуть, что после работы Никурадзе стало совершенно ясно, что при выполнении любых гидравлических расчетов нет надобности различать жидкости разного вида (как то делали ранее, когда предлагали отдельные расчетные формулы для вычисления потерь напора в случае воды, нефти, разных масел и т. п.). Именно из рассмотрения графика Никурадзе делается очевидным, что в гидравлике при определении потерь напора следует иметь в виду жидкость вообще, движение которой характеризуется безразмерным числом Рейнольдса определенной величины (зависящим, в частности, от таких физических характеристик рассматриваемой жидкости, как ее коэффициент вязкости и ее плотность).
§ 4-11. ПРАКТИЧЕСКИЕ СПОСОБЫ ОПРЕДЕЛЕНИЯ
Как было отмечено выше, различают шероховатые трубы, имеющие однозернистую шероховатость (с которыми работал Никурадзе) и трубы, имеющие разнозернистую шероховатость (когда выступы шероховатости имеют неодинаковую форму и размеры, расстояние между ними также различно). Трубы, обычно встречающиеся в практике, так называемые технические, имеют разнозернистую шероховатость или являются гладкими. Ниже поясним расчет технических труб. 1°. Напорные шероховатые технические трубы (трубы с разнозернистой шероховатостью). Для этих труб в 1938 г. Кольбрук на основании своих опытов, а также с учетом исследований других авторов, предложил формулу:
где Для квадратичной области сопротивления шероховатых труб формула (4-81′) упрощается и приобретает вид формулы Прандтля (предложенной им для шероховатых труб):
Для технических труб под величиной Рассматривают квадратичную область сопротивления и для этой области опытным путем, пользуясь формулой (4-70), находят для данной трубы величину λ. Затем по формуле (4-81") вычисляют искомое значение. Эквивалентная шероховатость зависит: а) от материала и способа изго-товления и соединения труб, б) от продолжительности эксплуатации труб, в процессе которой могут возникнуть коррозия стенок или инкрустации (образование наростов на стенках). Численные значения эквивалентной шероховатости
Таблица 4-2 Шероховатость
|
имеет большую величину;
= 0,5 (где 
— скорость по оси трубы), то в случае турбулентного движения в такой трубе обычно, как показывает опыт,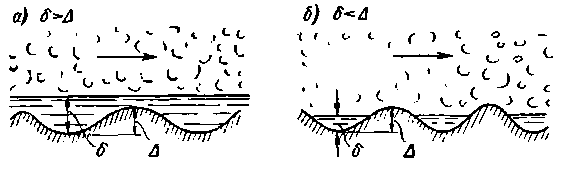 
, зависят от шероховатости стенок русла.
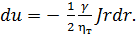(4-60)
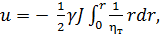(4-61)
определяется соотношением (4-56).
(4-62)
— радиус трубы; 
— расстояние от центра живого сечения до точки, где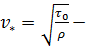
особое обозначение. Зависимость, аналогичная (4-62), была предложена Л. Прандтлем и для шероховатых труб.
, имеющую размерность скорости, называют скоростью трения или «динамической скоростью»; величину 
(4-63)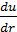
на оси трубы оказывается не равной нулю, что не соответствует
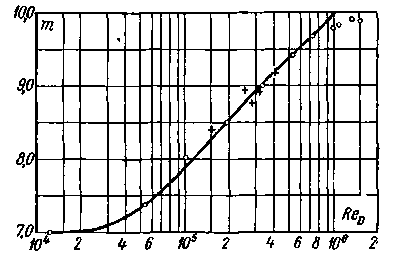
, (4-64)
— радиус трубы; 
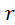— расстояние от центра живого сечения до точки, где измеряется скорость 
;m — знаменатель показателя степени, зависящий от числа Рейнольдса 
(рис. 4-18);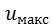 
— максимальная скорость (на оси трубы); об 
см. § 4-8,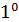 
.
будем находить по формуле (о коэффициенте λ см. ниже § 4-9):[21]
, (4-65)
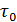(подтормаживающее движение жидкости), причем непосредственно на данной поверхности пластинки скорость u оказывается равной нулю.
(см. рисунок, участок живого сечения аm3) скорость u для сечения III-III будет изменяться существенно; за пределами же этого участка скорость u будет изменяться пренебрежимо мало, а следовательно, в этой области мы будем иметь (для сечения III-III)
для всех этих сечений будут различны:
и τ существенно отличаются от нуля;
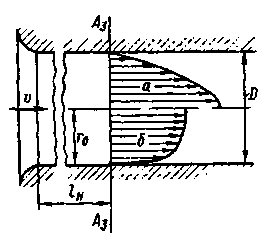
(4-66)
(см. § 4-2) может быть выражена через скоростной напор следующим образом:[25]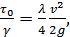
(4-67)
(4-68)
(4-69)
(4-70)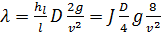
(4-71)
(4-72)
(4-73)
можно найти из (4-62). Подставляя такое выражение в (4-73), нетрудно найти зависимость для величины λ.
(4-74)
(4-75)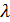
в случае шероховатых труб были предложены многими авторами. Прежде чем остановиться на пояснении тех из них, которые в настоящее время главным образом должны рекомендоваться для практического применения, осветим (в следующем параграфе) работу И. Никурадзе, обобщившего при помощи особого графика результаты всех исследований в области вопроса о потерях напора в круглых трубах.
на участке трубы длиной l.
, 
и ν, можно вычислять значения λ = f(ReD).
(4-76)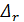
и ReD;
, или только от ReD;
величине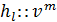 
(4-77)
,) I - зона ламинарного режима, С - зона неустойчивого (переходного) режима, II - область гладких русел турбулентной зоны, D - область доквадратичного сопротивления шероховатых русел турбулентной зоны, Е - область квадратичного сопротивления шероховатых русел турбулентной зоны
не зависит от шероховатости, так как все кривые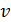
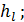она будет равна величине 
плюс соответствующий так называемый инерционный напор (поясняемый далее в гл. 9), который определить в данном случае нет возможности.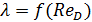
(4-78)
(4-79)
(4-80)
(4-81′)
— осредненная относительная шероховатость [см. формулу (4-76)]. По этой формуле был построен график[26] (рис. 4-25). Пользуясь этим графи-ком, можно определить коэффициент λ в случае технических труб для всех трех областей турбулентной зоны.
(4-81′′)
понимают некоторую среднюю высоту выступов шероховатости. Такую осредненную геометрическую характеристику 
Найденное таким образом среднее значение 
труб и каналов[27]