УРАВНЕНИЯ ЛАГРИНЖА И КЛЕРО
Если уравнение  второй степени относительно второй степени относительно  , то она имеет два решения относительно , то она имеет два решения относительно  и и  , непрерывных относительно , непрерывных относительно  и и  в некоторой области, а геометрически определяет в любой точке в некоторой области, а геометрически определяет в любой точке  этой области два направления интегральных кривых. этой области два направления интегральных кривых.
Такие дифференциальные уравнения  , кроме общего интеграла , кроме общего интеграла  и частных интегралов, иногда имеют еще особый интеграл, не содержащий произвольной постоянной и в то же время не получающийся из общего ни при каком значении постоянной. и частных интегралов, иногда имеют еще особый интеграл, не содержащий произвольной постоянной и в то же время не получающийся из общего ни при каком значении постоянной.
Особый интеграл, если он существует, можно получить исключив  из уравнений из уравнений  и и  или же исключив или же исключив 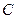 из общего интеграла из общего интеграла  и и  . Геометрический особый интеграл определяет огибающую семейства интегральных кривых. . Геометрический особый интеграл определяет огибающую семейства интегральных кривых.
Уравнение Лагранжа
 (6.1) (6.1)
где  интегрируется следующим образом: интегрируется следующим образом:
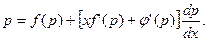
Это уравнение линейное относительно  и и  Решив его получим Решив его получим
 (6.2) (6.2)
Уравнения (6.1) и (6.2) будут параметрически определять общий интеграл. Исключив из них параметр 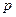 (если это возможно), получим общий интеграл в форме (если это возможно), получим общий интеграл в форме  . .
Уравнение Клеро
 (6.3) (6.3)
является частным случаем уравнения Лагранжа. Оно имеет общий интеграл  и особый, получающийся исключением параметра и особый, получающийся исключением параметра 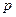 из уравнений из уравнений  и и 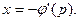
- ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ, ДОПУСКАЮЩИЕ ПОНИЖЕНИЕ ПОРЯДКА
Уравнение вида  решается последовательным решается последовательным  - кратным интегрированием правой части. При каждом интегрировании получается одна произвольная постоянная, а в окончательном результате - - кратным интегрированием правой части. При каждом интегрировании получается одна произвольная постоянная, а в окончательном результате -  произвольных постоянных. произвольных постоянных.
Уравнение 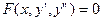 , не содержащее , не содержащее  в явной форме, подстановкой в явной форме, подстановкой
 приводится к виду приводится к виду
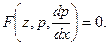
Уравнение 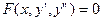 , не содержащее , не содержащее  в явной форме, подстановкой в явной форме, подстановкой  приводится к виду приводится к виду

- ЛИНЕЙНЫЕ ОДНОРОДНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ С
ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
Однородное линейное дифференциальное уравнение
 (8.1) (8.1)
где 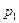 - функции - функции  , имеет общее решение вида , имеет общее решение вида
 (8.2) (8.2)
где  - линейно независимые частные решения уравнений (8.1), а - линейно независимые частные решения уравнений (8.1), а 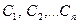 - произвольные постоянные. - произвольные постоянные.
Если коэффициенты  уравнения (8.1) постоянны, то частные решения уравнения (8.1) постоянны, то частные решения  находятся с помощью характеристического уравнения находятся с помощью характеристического уравнения
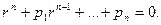 (8.3) (8.3)
1) Каждому вещественному корню  уравнения (8.3) кратности уравнения (8.3) кратности  соответствует соответствует  частных решений частных решений 
2) Каждой паре мнимых корней 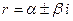 кратности кратности  соответствуют соответствуют  пар частных решений. пар частных решений.
- ЛИНЕЙНЫЕ НЕОДНОРОДНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ С
ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
Основное свойство. Пусть даны уравнения:
 - неоднородное, (9.1) - неоднородное, (9.1)
 - однородное, (9.2) - однородное, (9.2)
и пусть 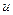 - общее решение уравнения (9.1) будет: - общее решение уравнения (9.1) будет:
 (9.3) (9.3)
Метод неопределенных коэффициентов.
При постоянных  частное решение частное решение  находится методом неопределенных коэффициентов в следующих случаях: находится методом неопределенных коэффициентов в следующих случаях:
1)  - многочлен; - многочлен;
2) 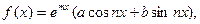
3)  есть сумма или произведение предыдущих функций. есть сумма или произведение предыдущих функций.
В этих случаях частное решение  имеет тот же вид, что и имеет тот же вид, что и  , отличаясь от нее только коэффициентами. , отличаясь от нее только коэффициентами.
Исключения составляют особые случаи, когда: 1)  - многочлен, но - многочлен, но 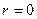 - корень характеристического уравнения кратности - корень характеристического уравнения кратности  ; 2) ; 2) 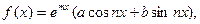 но но  есть корень характеристического уравнения кратности есть корень характеристического уравнения кратности  . В этих особых случаях . В этих особых случаях  отличается от отличается от  не только коэффициентами, но еще и множителем не только коэффициентами, но еще и множителем 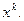
Метод вариации произвольных постоянных. Более общим приемом решения неоднородного линейного выражения является метод Лагранжа, или метод вариации произвольных постоянных.
Если  и и  - независимые частные решения уравнения - независимые частные решения уравнения  , то решение уравнения , то решение уравнения  по методу Лагранжа находится в виде по методу Лагранжа находится в виде  , где , где  и и  - функции - функции  , удовлетворяющие системе уравнений , удовлетворяющие системе уравнений
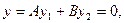

Отсюда
  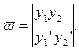
- ЛИНЕЙНОЕ ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ЭЙЛЕРА
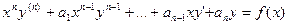
Частное решение однородного уравнения (при  ) можно найти в виде ) можно найти в виде  , где , где  - постоянное число. Для нахождения - постоянное число. Для нахождения  нужно подставить нужно подставить  в однородное дифференциальное уравнение и решить полученное характеристическое уравнение относительно в однородное дифференциальное уравнение и решить полученное характеристическое уравнение относительно  . При этом: . При этом:
1) Каждому вещественному корню  кратности кратности  соответствует соответствует  частных решений частных решений 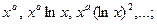
2) Каждой паре мнимых корней 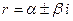 кратности кратности  соответствует соответствует  частных решений: частных решений:
 
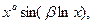 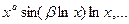
Неоднородное дифференциальное уравнение Эйлера решается методом вариации постоянных.
ЗАДАЧИ
1.Построить изображение поля направлений, определяемого уравнением
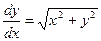 , с помощью окружностей, вдоль которых , с помощью окружностей, вдоль которых  Нарисовать приближенно интегральную кривую, проходящую через начало координат. Нарисовать приближенно интегральную кривую, проходящую через начало координат.
2.Построить изображение полей направлений, определяемых каждым из уравнений:
1)  2) 2)  3) 3) 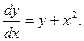
3.Построить изображение семейства 1) окружностей  2) парабол 2) парабол  и составить их дифференциальные уравнения. и составить их дифференциальные уравнения.
4.Решить уравнения:
1) 2) 2)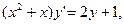
3) 4) 4)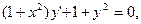
5) при при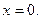
5.кривая проходит через точку 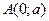 , ,  - произвольная ордината кривой. Определить кривую из условия, что площадь - произвольная ордината кривой. Определить кривую из условия, что площадь 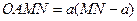 . .
6.Определить и построить кривую, проходящую через точки (1;1), для которой отрезок  , отсекаемый на оси , отсекаемый на оси 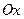 касательной к кривой в любой ее точке, равен квадрату абсциссы точки касания. касательной к кривой в любой ее точке, равен квадрату абсциссы точки касания.
7.Найти ортогональные траектории семейства гипербол  . .
8.Определить кривую, радиус – вектор любой точки которой равен отрезку нормали между кривой и осью 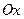 . .
9.Определить линию, если площадь, ограничена осями координат, этой линией и произвольной ее ординатой, равна 1/3 площади прямоугольника, построенного на конечной точки кривой.
10.Найти форму зеркала, отражающего все лучи, выходящие из данной точки, параллельно данному направлению.
Указание. Рассматривая плоское сечение зеркала, примем в нем данную точку за начало координат, а данное направление – за ось 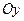 . Касательная к искомой кривой в точке . Касательная к искомой кривой в точке  образует равные углы с образует равные углы с 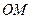 и осью и осью 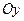 , т.е. Отсекает на оси , т.е. Отсекает на оси 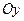 отрезок отрезок 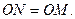
11.Решить дифференциальные уравнения:
1)  , 2) , 2) 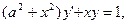
3)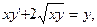 4) 4)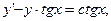
5) при при 6) 6)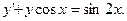
12.Определить кривую, проходящую через точку 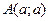 , если расстояние от начала координат до касательной в любой точке кривой равно абсциссе этой точки. , если расстояние от начала координат до касательной в любой точке кривой равно абсциссе этой точки.
13.Решить дифференциальные уравнения:
1)  2) 2) 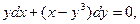
3)  4) 4) 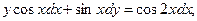
5)  6) 6) 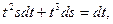
7)  8) 8) 
14. Найти интегрирующие множители:
1)  2) 2) 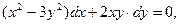
3)  4) 4) 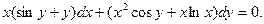
15. Решить уравнения, не содержащее явно одной из переменных:
1)  2) 2) 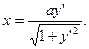
16.Решить уравнение:
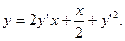
17.Найти кривую, касательные к которой образуют с осями координат треугольник постоянной площади, равной  . .
18.Найти кривую, касательной к которой отсекает на осях координат отрезки, сумма которых равна 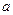 . .
19.Определить кривые, у которых радиус кривизны вдвое больше длинны нормали.
20.Определить кривые, у которых радиус кривизны равен длине нормали.
21.Решить уравнения:
1)    при при 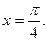
2)  , ,
3) 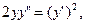
4) 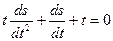
22.В интервале  определить кривую, касающуюся оси определить кривую, касающуюся оси 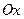 в начале координат, если кривизна ее в любой точке в начале координат, если кривизна ее в любой точке 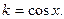
23.Решить уравнения:
1)  2) 2) 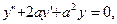
3)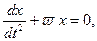 4) 4)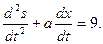
24.Два одинаковых груза подвешены к концу пружины. Под действием одного груза пружина удлиняется на 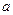 см. Определить движение первого груза, если второй оборвется (сопротивлением пренебречь). см. Определить движение первого груза, если второй оборвется (сопротивлением пренебречь).
25.Решить задачу 24 с учетом сопротивления, пропорционального скорости движения.
26.Решить уравнения:
1) 2) 2)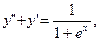
3) 4) 4)
5) 6) 6)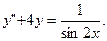
27.Единица массы движения по оси 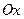 под действием постоянной силы под действием постоянной силы 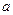 , направленной по оси, при сопротивлении движению, численно равном скорости движения. Найти закон движения если при , направленной по оси, при сопротивлении движению, численно равном скорости движения. Найти закон движения если при  имеем имеем  и скорость и скорость  . .
28.Следующие уравнения решить методом вариации произвольных постоянных:
1)  2) 2) 
3) 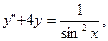 4) 4) 
29.Цилиндр радиуса 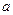 дм и массой дм и массой  кг плавает в воде при вертикальном положение оси. Найти период колебания, которое получается, если цилиндр немного погрузить в воду, а затем отпустить. Сопротивление движению принять приближенно равным нулю. кг плавает в воде при вертикальном положение оси. Найти период колебания, которое получается, если цилиндр немного погрузить в воду, а затем отпустить. Сопротивление движению принять приближенно равным нулю.
30.Полый железный шар с радиусами поверхностей 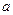 и 2 и 2 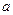 имеет постоянную температуру внутренней поверхности имеет постоянную температуру внутренней поверхности  и наружной и наружной  . Определить температуру внутри на любом расстоянии . Определить температуру внутри на любом расстоянии  от центра от центра 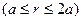 и при и при  . .
Указание. Скорость падения температуры  в проводнике со стационарным распределением температуры обратно пропорционально площади поперечно сечения. в проводнике со стационарным распределением температуры обратно пропорционально площади поперечно сечения.
31. Решить уравнения:
1)  2) 2) 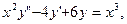
3)  4) 4) 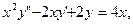
5)  6) 6) 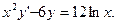
32.Найти частные решения дифференциальных уравнений:
1)  при при 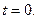
2)  при при 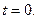
3)  при при 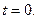
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|


 второй степени относительно
второй степени относительно  , то она имеет два решения относительно
, то она имеет два решения относительно  и
и  , непрерывных относительно
, непрерывных относительно  и
и  в некоторой области, а геометрически определяет в любой точке
в некоторой области, а геометрически определяет в любой точке  этой области два направления интегральных кривых.
этой области два направления интегральных кривых. и частных интегралов, иногда имеют еще особый интеграл, не содержащий произвольной постоянной и в то же время не получающийся из общего ни при каком значении постоянной.
и частных интегралов, иногда имеют еще особый интеграл, не содержащий произвольной постоянной и в то же время не получающийся из общего ни при каком значении постоянной. из уравнений
из уравнений  и
и  или же исключив
или же исключив 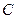 из общего интеграла
из общего интеграла  и
и  . Геометрический особый интеграл определяет огибающую семейства интегральных кривых.
. Геометрический особый интеграл определяет огибающую семейства интегральных кривых. (6.1)
(6.1) интегрируется следующим образом:
интегрируется следующим образом: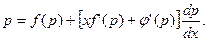
 Решив его получим
Решив его получим (6.2)
(6.2)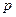 (если это возможно), получим общий интеграл в форме
(если это возможно), получим общий интеграл в форме  (6.3)
(6.3) и особый, получающийся исключением параметра
и особый, получающийся исключением параметра 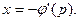
 решается последовательным
решается последовательным  - кратным интегрированием правой части. При каждом интегрировании получается одна произвольная постоянная, а в окончательном результате -
- кратным интегрированием правой части. При каждом интегрировании получается одна произвольная постоянная, а в окончательном результате - 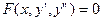 , не содержащее
, не содержащее  приводится к виду
приводится к виду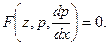

 (8.1)
(8.1)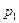 - функции
- функции  (8.2)
(8.2) - линейно независимые частные решения уравнений (8.1), а
- линейно независимые частные решения уравнений (8.1), а 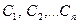 - произвольные постоянные.
- произвольные постоянные. уравнения (8.1) постоянны, то частные решения
уравнения (8.1) постоянны, то частные решения 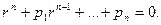 (8.3)
(8.3) уравнения (8.3) кратности
уравнения (8.3) кратности  соответствует
соответствует 
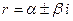 кратности
кратности  - неоднородное, (9.1)
- неоднородное, (9.1) - однородное, (9.2)
- однородное, (9.2)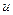 - общее решение уравнения (9.1) будет:
- общее решение уравнения (9.1) будет: (9.3)
(9.3) находится методом неопределенных коэффициентов в следующих случаях:
находится методом неопределенных коэффициентов в следующих случаях: - многочлен;
- многочлен;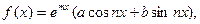
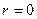 - корень характеристического уравнения кратности
- корень характеристического уравнения кратности  ; 2)
; 2)  есть корень характеристического уравнения кратности
есть корень характеристического уравнения кратности 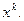
 - независимые частные решения уравнения
- независимые частные решения уравнения  , то решение уравнения
, то решение уравнения  по методу Лагранжа находится в виде
по методу Лагранжа находится в виде  , где
, где  и
и  - функции
- функции 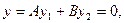



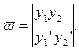
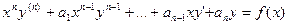
 ) можно найти в виде
) можно найти в виде  , где
, где  - постоянное число. Для нахождения
- постоянное число. Для нахождения 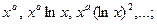


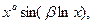
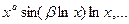
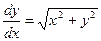 , с помощью окружностей, вдоль которых
, с помощью окружностей, вдоль которых  Нарисовать приближенно интегральную кривую, проходящую через начало координат.
Нарисовать приближенно интегральную кривую, проходящую через начало координат. 2)
2)  3)
3) 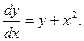
 2) парабол
2) парабол  и составить их дифференциальные уравнения.
и составить их дифференциальные уравнения. 2)
2)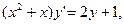
 4)
4)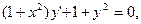
 при
при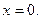
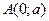 ,
,  - произвольная ордината кривой. Определить кривую из условия, что площадь
- произвольная ордината кривой. Определить кривую из условия, что площадь 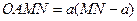 .
. , отсекаемый на оси
, отсекаемый на оси 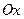 касательной к кривой в любой ее точке, равен квадрату абсциссы точки касания.
касательной к кривой в любой ее точке, равен квадрату абсциссы точки касания. .
.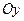 . Касательная к искомой кривой в точке
. Касательная к искомой кривой в точке  образует равные углы с
образует равные углы с 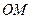 и осью
и осью 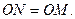
 , 2)
, 2) 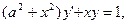
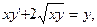 4)
4)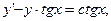
 при
при 6)
6)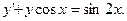
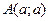 , если расстояние от начала координат до касательной в любой точке кривой равно абсциссе этой точки.
, если расстояние от начала координат до касательной в любой точке кривой равно абсциссе этой точки. 2)
2) 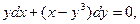
 4)
4) 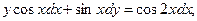
 6)
6) 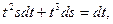
 8)
8) 
 2)
2) 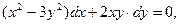
 4)
4) 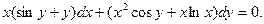
 2)
2) 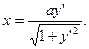
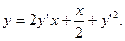
 .
.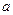 .
.

 при
при 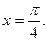
 ,
,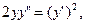
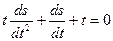
 определить кривую, касающуюся оси
определить кривую, касающуюся оси 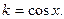
 2)
2) 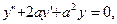
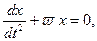 4)
4)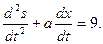
 2)
2)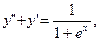
 4)
4)
 6)
6)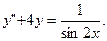
 имеем
имеем  и скорость
и скорость  .
. 2)
2) 
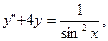 4)
4) 
 кг плавает в воде при вертикальном положение оси. Найти период колебания, которое получается, если цилиндр немного погрузить в воду, а затем отпустить. Сопротивление движению принять приближенно равным нулю.
кг плавает в воде при вертикальном положение оси. Найти период колебания, которое получается, если цилиндр немного погрузить в воду, а затем отпустить. Сопротивление движению принять приближенно равным нулю. и наружной
и наружной  . Определить температуру внутри на любом расстоянии
. Определить температуру внутри на любом расстоянии 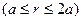 и при
и при  .
. в проводнике со стационарным распределением температуры обратно пропорционально площади поперечно сечения.
в проводнике со стационарным распределением температуры обратно пропорционально площади поперечно сечения. 2)
2) 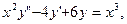
 4)
4) 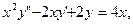
 6)
6) 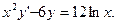
 при
при 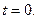
 при
при  при
при