КАСАТЕЛЬНАЯ ПЛОСКОСТЬ И НОРМАЛЬ К ПОВЕРХНОСТИ
Пусть поверхность задана уравнением  ; возьмем на ней точку ; возьмем на ней точку 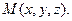
Уравнения нормали к поверхности этой точки будут:
 (10.1) (10.1)
Уравнение касательной плоскости:
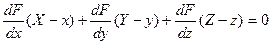 (10.2) (10.2)
В уравнениях (10.1) и (10.2) 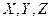 - текущие координаты нормали или касательной плоскости. - текущие координаты нормали или касательной плоскости.
Вектор 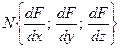 назовем нормальным вектором поверхности. назовем нормальным вектором поверхности.
Если на поверхности есть точка, в которой 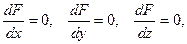 то она называется особой. В такой точке нет ни касательной, ни плоскости, ни нормали к поверхности. то она называется особой. В такой точке нет ни касательной, ни плоскости, ни нормали к поверхности.
СКАЛЯРНОЕ ПОЛЕ. ЛИНИИ И ПОВЕРХНОСТИ УРОВНЕЙ.
ПРОИЗВОДНАЯ В ДАННОМ НАПРАВЛЕНИИ. ГРАДИЕНТ
Уравнение 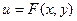 определяет определяет 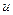 в каждой точке в каждой точке  некоторой области, которая называется полем скаляра некоторой области, которая называется полем скаляра 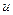 . Вдоль каждой из линий . Вдоль каждой из линий  где где 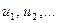 - постоянные, скаляр - постоянные, скаляр 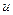 остается постоянным и меняется только при переходе точки остается постоянным и меняется только при переходе точки  с одной линии на другую. Эти линии называются изолиниями (изотермами, изобарами и т.п.) или линиями уровней. с одной линии на другую. Эти линии называются изолиниями (изотермами, изобарами и т.п.) или линиями уровней.
Уравнение  определяет поле скаляра и в некоторой части трехмерного пространства. Изоповерхностями, или поверхностями уровней будут: определяет поле скаляра и в некоторой части трехмерного пространства. Изоповерхностями, или поверхностями уровней будут:
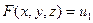 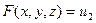 … …
Пусть точка 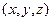 перемещается по прямой перемещается по прямой 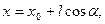  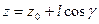 со скоростью со скоростью  Тогда скаляр Тогда скаляр  будут изменятся со скоростью будут изменятся со скоростью  где где 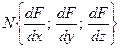 - нормальный вектор поверхности, а - нормальный вектор поверхности, а  - единичный вектор направления 1. - единичный вектор направления 1.
Производная
 
называется производной от функции  в данном направлении в данном направлении  . .
Градиентом скаляра  называется вектор называется вектор  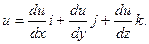
Градиент есть вектор скорости наибыстрейшего изменения скаляра 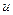 . .
ЭКСТРЕМУМ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ
Необходимые условия. Функция 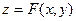 может иметь экстремум только в точках, в которых может иметь экстремум только в точках, в которых 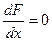 и и 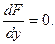 эти точки называются критическими. эти точки называются критическими.
Достаточные условия. Обозначим через 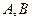 и и 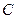 значения производных значения производных
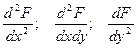 в критической точке в критической точке 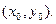
Тогда если:
1. 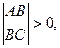 то то  при при 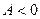 , , 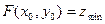 при при 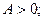
2. 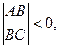 то экстремума нет; то экстремума нет;
3.  то экстремум может быть, а может и не быть (сомнительный случай). то экстремум может быть, а может и не быть (сомнительный случай).
Условный экстремум. Чтобы найти экстремум функции 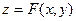 при условии, что при условии, что  и и  связаны уравнением связаны уравнением 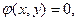 составим вспомогательную функцию составим вспомогательную функцию 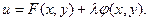
Координаты экстремальной точки 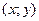 должны удовлетворять трем уравнениям: должны удовлетворять трем уравнениям:
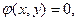 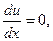 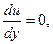
Из которых и находятся  и и 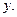
Задачи
- Построить геометрическое изображение однозначной функции
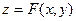 , определяемой уравнением , определяемой уравнением  , положенной в области , положенной в области 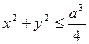 и отрицательной вне ее. Указать линию ее разрыва. и отрицательной вне ее. Указать линию ее разрыва. - Показать, что уравнение
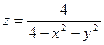 определяет определяет 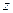 как бесчисленное множество однозначных функций как бесчисленное множество однозначных функций  и и  , из которых две непрерывны. Указать область определения всех этих функций, положительной в области , из которых две непрерывны. Указать область определения всех этих функций, положительной в области  и отрицательной вне ее. и отрицательной вне ее. - Доказать, что если
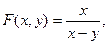 то то  - указать области определения функций:
1)  2) 2) 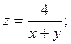 3) 3) 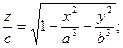 4) 4)  5) 5)  6) 6) 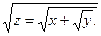
5. Показать, что уравнение 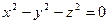 определяет определяет 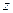 как бесчисленное множество функций как бесчисленное множество функций  и и  , из которых две непрерывны. Указать область определения всех этих функций и построить геометрическое изображение положительной непрерывной функции. Привести пример однозначной, но разрывной функции , из которых две непрерывны. Указать область определения всех этих функций и построить геометрическое изображение положительной непрерывной функции. Привести пример однозначной, но разрывной функции 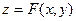 , определяемой тем же уравнением , определяемой тем же уравнением 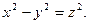
6. Доказать, что если  , то , то 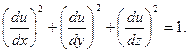
7. Доказать, что если 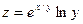 , то , то 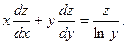
8. Доказать, что если  то то 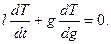
9. Доказать, что если  то то 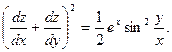
10. Катеты прямоугольного треугольника, измеренные с точностью до 0,1 см, оказались равными 7,5 см и 18 см. Определить абсолютную погрешность при вычислении гипотенузы.
11. При деформации цилиндра его радиус 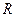 увеличился с 20 см до 20,5 см, а высота увеличился с 20 см до 20,5 см, а высота  уменьшилась со 100 см до 98 см. найти приближенно изменение объема уменьшилась со 100 см до 98 см. найти приближенно изменение объема 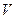 по формуле по формуле 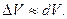
12. Найти значение  и и 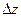 для функции для функции 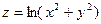 , когда , когда  изменяется от 2 до 2,1; а изменяется от 2 до 2,1; а  - от 1 до 0,9. - от 1 до 0,9.
13. Подсчитать приблизительно изменения функции 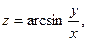 когда когда  изменяется от 5 до 4,5; а изменяется от 5 до 4,5; а  - от 3 до 3,3. - от 3 до 3,3.
14. Найти  из уравнений: из уравнений:
1) 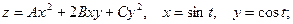
2) 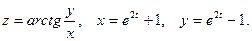
15. Доказать, что если  , где , где 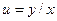 , то , то
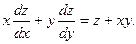
16. Доказать, что если  где где  , то , то
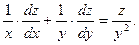
17. Пусть 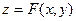 . Выразить . Выразить 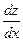 и и 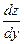 через через 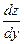 и и 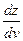 , если 1) , если 1) 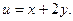
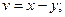 2) 2) 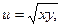 
18. 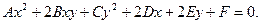
Найти угловой коэффициент касательной к кривой.
19. Доказать, что если  , то , то 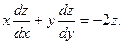
20. Показать, что дифференциальному уравнению 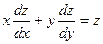 удовлетворяет неявная функция удовлетворяет неявная функция 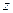 , определяемая уравнением (конических поверхностей) , определяемая уравнением (конических поверхностей) 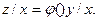
21. Найти 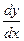 из уравнений: из уравнений:
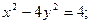 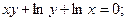 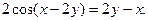
22. Показать, что функция  при любых дважды дифференцируемых функциях при любых дважды дифференцируемых функциях 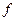 и и 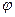 удовлетворяет дифференциальному уравнению удовлетворяет дифференциальному уравнению
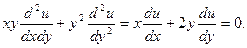
23. Пусть  Найти Найти 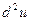 и и 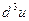 . .
24. Найти частные производные второго порядка функции 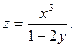
25. Доказать, что если  , то , то 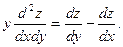
26. Определить области расположения, точки пересечения с осями координат, особые точки кривых и построить кривые:
1)  3) 3) 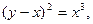
2) 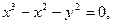 4) 4) 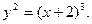
27. Найти точки пересечения с осями координат, 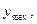 особую точку и симптому кривой особую точку и симптому кривой  и построить кривую. и построить кривую.
28. Определить области расположения, особые точки и асимптоты кривых:
1)  4) 4) 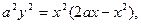
2)  5) 5) 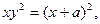
3) 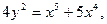 6) 6) 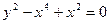 . .
29. Найти огибающую семейства парабол, имеющих ось симметрии, параллельную оси 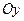 , и проходящих через точки , и проходящих через точки 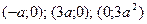 при различных при различных 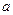 . .
30. Отрезок постоянной длинны 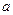 скользит своими концами по координатным осям. Найти огибающую семейства таких отрезков. скользит своими концами по координатным осям. Найти огибающую семейства таких отрезков.
31. Найти огибающую семейства окружностей, проходящих через начало координат и имеющих центр на параболе 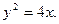
32. Из начала координат выпускается снаряд с начальной скоростью 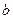 под углом под углом  к оси к оси 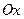 . Найти огибающую семейства траекторий при различных . Найти огибающую семейства траекторий при различных  . .
33. Найти огибающую 1) семейства прямых 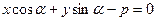 при постоянном при постоянном 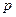 ; 2) семейства прямых ; 2) семейства прямых  3) семейства кубических парабол 3) семейства кубических парабол 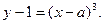
34. Написать уравнения касательной плоскости к поверхности:
1)  в точке (1;1;3), в точке (1;1;3),
2) 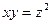 в точке в точке 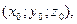
3)  в точке в точке 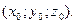 
35. Показать, что касательная плоскость к поверхности  в точке на ней в точке на ней  определяется уравнением определяется уравнением 
36. Найти углы с осями координат нормали к поверхности  в точке (2;2;0). в точке (2;2;0).
37. Найти расстояние начала координат от касательной плоскости к коноиду 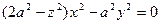 в точке в точке 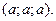
38. Найти производную функции  в точке (1;1;1) в направлении в точке (1;1;1) в направлении 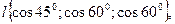 и найти и найти  в той же точке и его длину. Построить поверхности уровней. в той же точке и его длину. Построить поверхности уровней.
39. Пусть 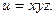 Найти производную Найти производную  в направлении, составляющим с осями координат равные углы, в любой точке и точке (1;2;1). в направлении, составляющим с осями координат равные углы, в любой точке и точке (1;2;1).
40. Построить поверхности уровней скаляра 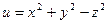 , определить , определить  на поверхности, проходящей через начало координат, и построить его в трех точках этой поверхности, в которых на поверхности, проходящей через начало координат, и построить его в трех точках этой поверхности, в которых 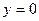 и и  . .
41. Пусть 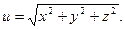 Найти Найти  и его длину. и его длину.
42. Построить изоповерхности поля функции  и найти производную от и найти производную от 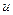 в точке в точке 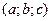 в направлении радиус – вектора этой точки. в направлении радиус – вектора этой точки.
43. 1) В эллипс  вписать равнобедренный треугольник с основанием, параллельным большой оси, так, чтобы площадь треугольника была наибольшей. вписать равнобедренный треугольник с основанием, параллельным большой оси, так, чтобы площадь треугольника была наибольшей.
2) Ось 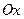 расположена на границе двух сред. По какому пути должен пройти луч света из точки расположена на границе двух сред. По какому пути должен пройти луч света из точки 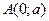 в точку в точку 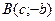 , чтобы затратить на прохождение этого расстояния наименьшее время , чтобы затратить на прохождение этого расстояния наименьшее время 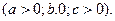
Указание.Нужно найти минимум функции  при условии, при условии, 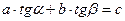 где где  и и  - скорости света в двух средах, а - скорости света в двух средах, а  и и  - углы падения и преломления. - углы падения и преломления.
44. Найти экстремумы функций:
1) 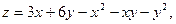
2) 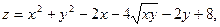
3) 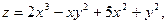
4) 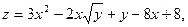
5) 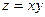 при условии, что при условии, что 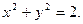
45. Найти наибольший объем прямоугольного параллелепипеда при условии, что длина его диагонали равна 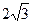 . .
46. 1) На параболе 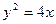 найти точку, наименее удаленную от прямой найти точку, наименее удаленную от прямой 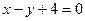 . .
2) В эллипс 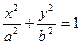 вписан прямоугольник наибольшей площади. Найти эту площадь. вписан прямоугольник наибольшей площади. Найти эту площадь.
47. Определить размеры конуса наибольшего объема при условии, что его боковая поверхность 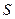 . .
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|


 ; возьмем на ней точку
; возьмем на ней точку 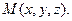
 (10.1)
(10.1)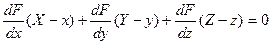 (10.2)
(10.2)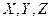 - текущие координаты нормали или касательной плоскости.
- текущие координаты нормали или касательной плоскости.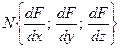 назовем нормальным вектором поверхности.
назовем нормальным вектором поверхности.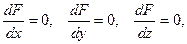 то она называется особой. В такой точке нет ни касательной, ни плоскости, ни нормали к поверхности.
то она называется особой. В такой точке нет ни касательной, ни плоскости, ни нормали к поверхности.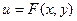 определяет
определяет 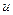 в каждой точке
в каждой точке  некоторой области, которая называется полем скаляра
некоторой области, которая называется полем скаляра  где
где 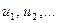 - постоянные, скаляр
- постоянные, скаляр  определяет поле скаляра и в некоторой части трехмерного пространства. Изоповерхностями, или поверхностями уровней будут:
определяет поле скаляра и в некоторой части трехмерного пространства. Изоповерхностями, или поверхностями уровней будут: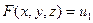
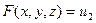 …
…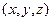 перемещается по прямой
перемещается по прямой 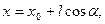

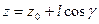 со скоростью
со скоростью  Тогда скаляр
Тогда скаляр  где
где  - единичный вектор направления 1.
- единичный вектор направления 1.


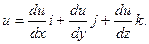
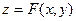 может иметь экстремум только в точках, в которых
может иметь экстремум только в точках, в которых 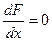 и
и 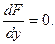 эти точки называются критическими.
эти точки называются критическими.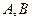 и
и 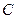 значения производных
значения производных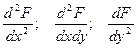 в критической точке
в критической точке 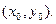
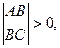 то
то  при
при 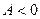 ,
, 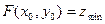 при
при 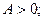
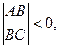 то экстремума нет;
то экстремума нет; то экстремум может быть, а может и не быть (сомнительный случай).
то экстремум может быть, а может и не быть (сомнительный случай). и
и  связаны уравнением
связаны уравнением 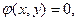 составим вспомогательную функцию
составим вспомогательную функцию 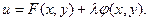
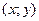 должны удовлетворять трем уравнениям:
должны удовлетворять трем уравнениям: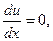
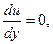
 и
и 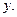
 , положенной в области
, положенной в области 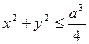 и отрицательной вне ее. Указать линию ее разрыва.
и отрицательной вне ее. Указать линию ее разрыва.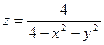 определяет
определяет 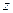 как бесчисленное множество однозначных функций
как бесчисленное множество однозначных функций  и отрицательной вне ее.
и отрицательной вне ее.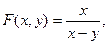 то
то 
 2)
2) 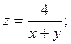 3)
3) 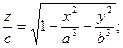 4)
4)  5)
5)  6)
6) 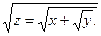
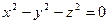 определяет
определяет 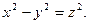
 , то
, то 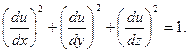
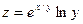 , то
, то 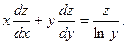
 то
то 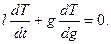
 то
то 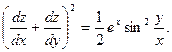
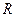 увеличился с 20 см до 20,5 см, а высота
увеличился с 20 см до 20,5 см, а высота  уменьшилась со 100 см до 98 см. найти приближенно изменение объема
уменьшилась со 100 см до 98 см. найти приближенно изменение объема 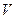 по формуле
по формуле 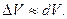
 и
и 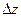 для функции
для функции 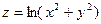 , когда
, когда 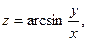 когда
когда  из уравнений:
из уравнений: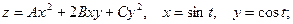
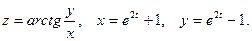
 , где
, где 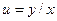 , то
, то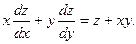
 где
где  , то
, то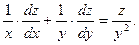
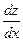 и
и 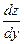 через
через 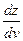 , если 1)
, если 1) 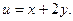
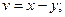 2)
2) 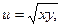

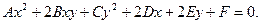
 , то
, то 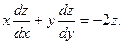
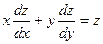 удовлетворяет неявная функция
удовлетворяет неявная функция 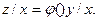
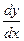 из уравнений:
из уравнений: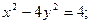
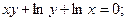
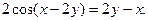
 при любых дважды дифференцируемых функциях
при любых дважды дифференцируемых функциях 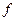 и
и 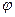 удовлетворяет дифференциальному уравнению
удовлетворяет дифференциальному уравнению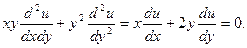
 Найти
Найти 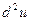 и
и 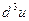 .
.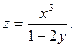
 , то
, то 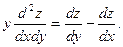
 3)
3) 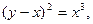
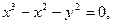 4)
4) 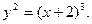
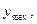 особую точку и симптому кривой
особую точку и симптому кривой  и построить кривую.
и построить кривую. 4)
4) 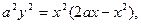
 5)
5) 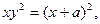
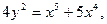 6)
6) 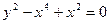 .
.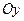 , и проходящих через точки
, и проходящих через точки 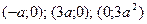 при различных
при различных 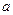 .
.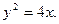
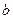 под углом
под углом  к оси
к оси 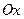 . Найти огибающую семейства траекторий при различных
. Найти огибающую семейства траекторий при различных 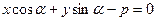 при постоянном
при постоянном 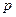 ; 2) семейства прямых
; 2) семейства прямых  3) семейства кубических парабол
3) семейства кубических парабол 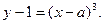
 в точке (1;1;3),
в точке (1;1;3),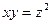 в точке
в точке 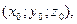
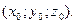
 в точке на ней
в точке на ней  определяется уравнением
определяется уравнением 
 в точке (2;2;0).
в точке (2;2;0).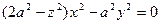 в точке
в точке 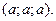
 в точке (1;1;1) в направлении
в точке (1;1;1) в направлении 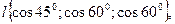 и найти
и найти  в той же точке и его длину. Построить поверхности уровней.
в той же точке и его длину. Построить поверхности уровней.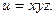 Найти производную
Найти производную  в направлении, составляющим с осями координат равные углы, в любой точке и точке (1;2;1).
в направлении, составляющим с осями координат равные углы, в любой точке и точке (1;2;1).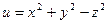 , определить
, определить 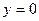 и
и  .
.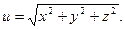 Найти
Найти  и найти производную от
и найти производную от 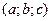 в направлении радиус – вектора этой точки.
в направлении радиус – вектора этой точки. вписать равнобедренный треугольник с основанием, параллельным большой оси, так, чтобы площадь треугольника была наибольшей.
вписать равнобедренный треугольник с основанием, параллельным большой оси, так, чтобы площадь треугольника была наибольшей.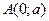 в точку
в точку 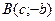 , чтобы затратить на прохождение этого расстояния наименьшее время
, чтобы затратить на прохождение этого расстояния наименьшее время 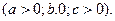
 при условии,
при условии, 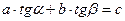 где
где  и
и  - скорости света в двух средах, а
- скорости света в двух средах, а  - углы падения и преломления.
- углы падения и преломления.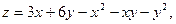
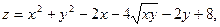
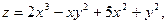
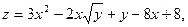
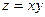 при условии, что
при условии, что 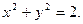
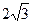 .
.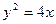 найти точку, наименее удаленную от прямой
найти точку, наименее удаленную от прямой 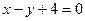 .
.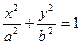 вписан прямоугольник наибольшей площади. Найти эту площадь.
вписан прямоугольник наибольшей площади. Найти эту площадь. .
.