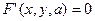ЧАСТНЫЕ ПРОИЗВОДНЫЕ, ПОЛНЫЕ
ДИФФЕРЕНЦИАЛЫ И ИХ ПРИЛОЖЕНИЯ
- ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ И ИХ ГЕОМЕТРИЧЕСКОЕ
ИЗОБРАЖЕНИЕ
Определение. Переменная 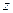 называется однозначной функцией переменных называется однозначной функцией переменных  и и  , если каждой паре значений , если каждой паре значений  и и  в некоторой области их изменений поставлено в соответствие одно значение в некоторой области их изменений поставлено в соответствие одно значение 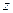 . Функциональную зависимость . Функциональную зависимость 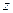 от от  и и  записывают в виде записывают в виде
 . (1.1) . (1.1)
Геометрическое изображение. Уравнение (1) геометрически определяет некоторую поверхность. Пара значений  и и  определяет на плоскости определяет на плоскости  точку точку  , а , а 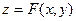 - аппликату соответствующей точки - аппликату соответствующей точки  на поверхности. Поэтому говорят, что на поверхности. Поэтому говорят, что 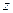 есть функция точки есть функция точки  , и пишут , и пишут  . .
Предел функции  , если разность , если разность  - -  есть бесконечно малая, когда есть бесконечно малая, когда  при любом способе приближения при любом способе приближения  к к  (например, по любой линии). (например, по любой линии).
Непрерывность функции. Функция  называется непрерывной в точке называется непрерывной в точке  если, если,  Иначе говоря, функция Иначе говоря, функция  непрерывна в некоторой точке непрерывна в некоторой точке 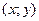 , если , если
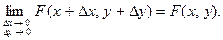
- ЧАСТНЫЕ ПРОИЗВОДНЫЕ ПЕРВОГО ПОРЯДКА
Производная функции  по по  , найденная в предложении, что остается постоянным, называется частной производной , найденная в предложении, что остается постоянным, называется частной производной 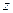 по по  и обозначается и обозначается 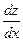 или или 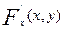 . .
Аналогично определяется и обозначается частная производная 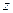 по по  : : 
- ПОЛНЫЙ ДИФФЕРЕНЦИАЛ ПЕРВОГО ПОРЯДКА
Если функция  имеет в точке имеет в точке 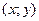 непрерывные частные производные, то ее полное приращение может быть представлено в виде непрерывные частные производные, то ее полное приращение может быть представлено в виде
 (3.1) (3.1)
где  при при  . Тогда выражение . Тогда выражение  есть главная часть полного приращения есть главная часть полного приращения 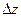 ; она называется полным дифференциалом функции и обозначается ; она называется полным дифференциалом функции и обозначается  : :
 (3.2) (3.2)
Полагая в формуле (3.2) 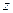 равным 1) равным 1)  ; 2) ; 2)  , найдем , найдем  , ,  . Поэтому . Поэтому
 (3.3) (3.3)
Из (3.1) следует что
 (3.4) (3.4)
т.е. при достаточно малых  и и  полное приращение функции приближенно равно ее полному дифференциалу. полное приращение функции приближенно равно ее полному дифференциалу.
Функция  называется дифференцируемой в точке называется дифференцируемой в точке 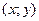 , если она имеет в этой точке полным дифференциалом. , если она имеет в этой точке полным дифференциалом.
- ПРОИЗВОДНЫЕ СЛОЖНЫХ ФУНКЦИЙ
Если  то то 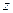 называется сложной функцией от называется сложной функцией от  . При этом . При этом
 (4.1) (4.1)
Если функция  и и 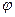 дифференцируемы. дифференцируемы.
Если 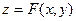 , где , где  , если функции , если функции  и и 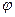 дифференцируемы, то дифференцируемы, то
 (4.2) (4.2)
ПРОИЗВОДНЫЕ НЕЯВНЫХ ФУНКЦИЙ
Уравнение  , имеющее решение , имеющее решение 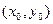 , определяет в окрестности , определяет в окрестности  переменную переменную  как непрерывную функцию как непрерывную функцию  при условии, что производная при условии, что производная  и непрерывна в некоторой окрестности точки и непрерывна в некоторой окрестности точки 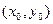 . .
 Символично это равенство можно записать так: Символично это равенство можно записать так:
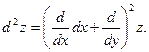
Аналогично 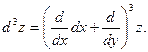 и т.д. и т.д.
ИНТЕГРИРОВАНИЕ ПОЛНЫХ ДИФФЕРЕНЦИАЛОВ
Чтобы выражение  где где  и и  - дифференцируемые функции - дифференцируемые функции  и и  , было полным дифференциалом , было полным дифференциалом  , необходимо и достаточно выполнение условия , необходимо и достаточно выполнение условия 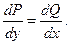
Для нахождения 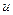 из условий из условий  и и  получим получим 
 Выписав из первого предложения все известные члены, а из второго – члены с Выписав из первого предложения все известные члены, а из второго – члены с  , недостающие в первом, получим функцию , недостающие в первом, получим функцию 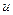 . .
Чтобы выражение  где где  - дифференцируемые функции от - дифференцируемые функции от  и и 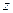 , было полным дифференциалом , было полным дифференциалом  , необходимо и достаточно выполнение условий: , необходимо и достаточно выполнение условий:
  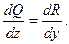
Для нахождения имеем:
  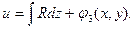
Выписав из первого выражения все известные члены, а из второго и третьего – недостающие члены с  и и 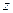 , получим функцию , получим функцию 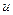 . .
Нахождение функции по ее полному дифференциалу называется интегрированием полного дифференциала.
ОСОБЫЕ ТОЧКИ ПЛОСКОЙ КРИВОЙ
Точка кривой  называется особой, если в этой точке называется особой, если в этой точке 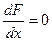 и и  . .
Угловой коэффициент  касательной в точке находится из уравнения касательной в точке находится из уравнения  где где  - значения производных - значения производных  и и 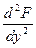 в этой особой точке. в этой особой точке.
При этом возможно три случая:
1.  - две касательных; точка называется узлом. - две касательных; точка называется узлом.
2.  - нет касательной; точка изолирована. - нет касательной; точка изолирована.
3.  - или изолированная точка, или точка возврата, самосоприкосновения существует одна общая касательная к двум ветвям прямой. - или изолированная точка, или точка возврата, самосоприкосновения существует одна общая касательная к двум ветвям прямой.
Чтобы в третьем, сомнительном, случае решить вопрос окончательно, нужно узнать, имеются ли точки кривой в сколь угодно малой окрестности исследуемой точки.
ОГИБАЮЩАЯ СЕМЕЙСТВА ПЛОСКИХ КРИВЫХ
Кривая называется огибающей семейства кривых  , если: , если:
1. она касается каждой кривой семейства;
2. каждая ее точка является точкой ее касания с кривой семейства, отличной от нее самой.
Огибающая семейства кривых  , если она существует, находится исключением параметра , если она существует, находится исключением параметра  из уравнений из уравнений
 и и 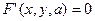
Может, однако, случится, что полученная этим способом кривая будет не огибающей, а геометрическим местом особых точек кривых семейства.
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|


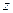 называется однозначной функцией переменных
называется однозначной функцией переменных  и
и  , если каждой паре значений
, если каждой паре значений  . (1.1)
. (1.1) точку
точку  , а
, а 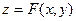 - аппликату соответствующей точки
- аппликату соответствующей точки  на поверхности. Поэтому говорят, что
на поверхности. Поэтому говорят, что  .
. , если разность
, если разность  -
-  есть бесконечно малая, когда
есть бесконечно малая, когда  при любом способе приближения
при любом способе приближения  к
к  (например, по любой линии).
(например, по любой линии). называется непрерывной в точке
называется непрерывной в точке  Иначе говоря, функция
Иначе говоря, функция 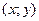 , если
, если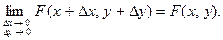
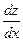 или
или 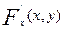 .
.
 (3.1)
(3.1) при
при  . Тогда выражение
. Тогда выражение  есть главная часть полного приращения
есть главная часть полного приращения 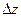 ; она называется полным дифференциалом функции и обозначается
; она называется полным дифференциалом функции и обозначается  :
: (3.2)
(3.2) ,
,  . Поэтому
. Поэтому (3.3)
(3.3) (3.4)
(3.4) и
и  полное приращение функции приближенно равно ее полному дифференциалу.
полное приращение функции приближенно равно ее полному дифференциалу. то
то  . При этом
. При этом (4.1)
(4.1) и
и 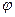 дифференцируемы.
дифференцируемы. , если функции
, если функции  (4.2)
(4.2) , имеющее решение
, имеющее решение 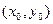 , определяет в окрестности
, определяет в окрестности  переменную
переменную  и непрерывна в некоторой окрестности точки
и непрерывна в некоторой окрестности точки  Символично это равенство можно записать так:
Символично это равенство можно записать так: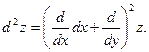
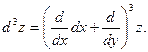 и т.д.
и т.д. где
где  - дифференцируемые функции
- дифференцируемые функции  , необходимо и достаточно выполнение условия
, необходимо и достаточно выполнение условия 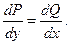
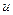 из условий
из условий  и
и  получим
получим 
 Выписав из первого предложения все известные члены, а из второго – члены с
Выписав из первого предложения все известные члены, а из второго – члены с  где
где  - дифференцируемые функции от
- дифференцируемые функции от  и
и 

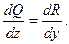


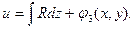
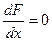 и
и  .
. касательной в точке находится из уравнения
касательной в точке находится из уравнения  где
где  - значения производных
- значения производных  и
и 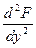 в этой особой точке.
в этой особой точке. - две касательных; точка называется узлом.
- две касательных; точка называется узлом. - нет касательной; точка изолирована.
- нет касательной; точка изолирована. - или изолированная точка, или точка возврата, самосоприкосновения существует одна общая касательная к двум ветвям прямой.
- или изолированная точка, или точка возврата, самосоприкосновения существует одна общая касательная к двум ветвям прямой. , если:
, если: из уравнений
из уравнений