
|
|
ГИПЕРБОЛИЧЕСКИЕ ПОДСТАНОВКИЭЛЕМЕНТЫ НЕПРЕРЫВНОЙ МАТЕМАТИКИ Под редакцией А.К. Шлепкина
Оглавление Переменные величины и функции…………………………………………………….4 Пределы последовательности и функции. Бесконечно малые и бесконечно большие………………………………………………………………………………….4 Свойства пределов. Раскрытие неопределенности вида Предел отношения Сравнение бесконечно малых………………………………………………………….5 Непрерывность функции……………………………………………………………….6 Асимптоты……………………………………………………………………………....6 Число Производные алгебраических и тригонометрических функций…………………….7 Производная сложных функций……………………………………………………….7 Касательная и нормаль к плоской кривой…………………………………………….8 Случай недифференцируемости непрерывной функции………………………………………………………………………………….8 Производные логарифмических и показательных функций…………………………9 Производные обратных тригонометрических функций……………………………...9 Производные гиперболических функций……………………………………………..9 Производные высших порядков……………………………………………………….9 Производная неявной функции………………………………………………………...9 Дифференциал функции………………………………………………………………10 Параметрические уравнения кривой…………………………………………………10 Задачи…………………………………………………………………………………..11 Неопределенный интеграл. Интегрирование разложением………………………...15 Интегрирование подстановкой и непосредственное………………………………..16 Интегрирование по частям……………………………………………………………16 Интегрирование тригонометрических функций…………………………………….17 Интегрирование рациональных алгебраических функций…………………………17 Интегрирование некоторых иррациональных алгебраических функций………….17 Интегрирование некоторых трансцендентных функций…………………………...18 Интегрирование гиперболических функций. Гиперболические подстановки…….18 Вычисление определенного интеграла………………………………………………19 Вычисление площадей………………………………………………………………...20 Объем тела вращения………………………………………………………………….21 Длина дуги плоской кривой…………………………………………………………..21 Площадь поверхности вращения……………………………………………………..22 Несобственные интегралы…………………………………………………………….22 Среднее значение функции…………………………………………………………...23 Формула трапеции и формула Симпсона……………………………………………23 Неопределенный интеграл. Задачи…………………………………………………...24 Определенный интеграл. Задачи……………………………………………………...25 Частные производные, полные дифференциалы и их приложения………………..27 Частные производные первого порядка……………………………………………...28 Полный дифференциал первого порядка…………………………………………….28 Производные сложных функций……………………………………………………..29 Производные неявных функций……………………………………………………...29 Частные производные и полные дифференциалы высших порядков……………...30 Интегрирование полных дифференциалов…………………………………………..30 Особые точки плоских кривых……………………………………………………….30 Касательная плоскость и нормаль к поверхности…………………………………...31 Скалярное поле. Линии и поверхности уровней. Производная в данном направлении. Градиент………………………………………………………………..32 Экстремум функции двух переменных………………………………………………32 Задачи…………………………………………………………………………………..33 Понятие о дифференциальном уравнении…………………………………………...37 дифференциальном уравнение первого порядка с разделяющимися переменными. Ортогональные траектории…………………………………………………………...38 Дифференциальном уравнение первого порядка: однородное, линейное, Бернулли………………………………………………………………………………..39 Дифференциальном уравнение, содержащие дифференциалы произведения и частного………………………………………………………………………………...39 Дифференциальном уравнении первого порядка, не разрешенные относительно производной. Уравнение Лагринжа и Клеро………………………………………...40 Дифференциальном уравнении высшего порядка, допускающие понижение порядка…………………………………………………………………………………41 Линейные однородные дифференциальные уравнения с постоянными коэффициентами……………………………………………………………………….42 Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами……………………………………………………………………….42 Линейные дифференциальные уравнения Эйлера…………………………………..43 Задачи…………………………………………………………………………………..44
ВВЕДЕНИЕ В АНАЛИЗ
1о. Отрезки и интервалы. Множество чисел х, удовлетворяющих неравенствам а < х < b, называется интервалом и обозначается (a, b). Множество чисел x, удовлетворяющих неравенствам a £ x £ b, называется отрезком и обозначается [a, b]. Эквивалентные неравенства (при a > 0) x2 < a2, или –a < x < a определяют интервал, симметричный относительно нуля. 2о. Переменные величины и функции. Если каждому значению переменной x поставлено в соответствие одно число, то переменная y, определяемая совокупностью этих чисел, называется однозначной функцией x. Переменная x называется при этом аргументом, а данная совокупность значений аргумента – областью определения функции. То, что y есть функция x, символически записывают в виде y = f(x), или y = F(x), или y =
§2. Пределы последовательности и функции. Бесконечно малые и бесконечно большие.
1о. Числовая последовательность. Пусть каждому натуральному числу n = 1,2,3,… по некоторому закону поставлено в соответствие число xn. Тогда говорят, что определена последовательность чисел x1,x2,x3…или, короче, последовательность {xn} = { x1,x2,x3…}. Отдельные числа последовательности {xn} называются её элементами. Говорят ещё, что переменная xn пробегает значение последовательности {xn}. 2о. Предел последовательности (предел переменной). Число, а называется пределом последовательности {xn} или пределом переменной xn (обозначается xn ® а), если для всякого 3о. Предел функции. Пусть функция f(x) определена в некоторой Если x → a и при этом х < а то пишут x → a – 0; аналогично, если x → a и при этом х > а, то пишут x → a + 0. Числа f(a - 0) = limx → a – 0 f(x) и f(a + 0) = limx → a + 0 f(x) называются соответственно пределом слева функции f(x) в точке а и пределом справа функции f(x) в точке а. Для существования предела функции f(x) при x → a необходимо и достаточно, чтобы было f(a - 0) = f(a + 0). Вместо x → 0 – 0 и x → 0 + 0 пишут x → – 0 и x → + 0 соответственно. 4о Бесконечно малые. Если limx → aa(х) = 0, т.е. если |a(х)| < e при 0 < |х - а| < d(e), то функция a(х) называется бесконечно малой при x → a. Аналогично определяется бесконечно малая a(х) при x → ¥. 5о Бесконечно большие. Если для любого сколь угодно большого числа N существует такое d(N), что при 0 < |х - а| < d(N) выполнено равенство |f(x)| >N, то функция f(x) называется бесконечно большой при x → a. Аналогично определяется бесконечно большая f(x) при x → ¥.
§3. Свойства пределов. Раскрытие неопределенностей вида
Это свойство применяется при раскрытии неопределённостей вида Например, §4. Предел отношения
Если угол
§7. Сравнение бесконечно малых.
I. Если II. Если III. Если
а) Разность двух эквивалентных бесконечно малых есть бесконечно малая высшего порядка относительно каждой из них. б) Если из суммы нескольких бесконечно малых разных порядков отбросить бесконечно малые высшего порядка, то оставшаяся часть, называемая главной, эквивалентна всей сумме. Из первого свойства следует, что эквивалентные бесконечно малые могут сделаться приближенно равными со сколь угодно малой относительной погрешностью. Поэтому знак
§8. Непрерывность функции.
Это определение содержит такие четыре условия непрерывности: 1) 2) должны существовать конечные пределы 3) эти пределы (слева и справа) должны быть одинаковыми; 4) эти пределы должны быть равны Функция называется непрерывной на отрезке Элементарные функции: степенная
1) Разрыв I рода – когда существуют конечные пределы 2) Разрыв II рода – когда Например, функция
§9. Асимптоты.
Асимптотой кривой называется прямая, к которой неограниченно приближается точка кривой при ее удалении по кривой в бесконечность. I. Если Например, кривая II. Если в правой части уравнения кривой y = f(x) можно выделить линейную часть y = f(x) = kx + b + a(x) так, что оставшиеся часть a(x)→ 0, когда x → ± ∞, то прямая y = kx + b есть асимптота кривой. Примеры 1) кривая у = III. Если существуют конечные пределы
§10. Число e. Числом e называется предел
Это число иррациональное и приближенно равно e = 2,71828… Логарифмы с основанием e называются натуральными и обозначаются Десятичный логарифм:
ПРОИЗВОДНАЯ И ДЕФФЕРЕНЦИАЛ
§1. Производные алгебраических и тригонометрических функций.
Если этот предел конечный, то функция Если же предел (1) равен Производная обозначается y’ или f’(x), или 1) (c)’ = 0; 2) 4) 6) 8) 10)
§2. Производная сложной функции.
Если,
Формулы предыдущего параграфа примут теперь общий вид: 1) 5)
§3. Касательная и нормаль к плоской кривой.
Угловой коэффициент касательной к кривой
Это число
Уравнение нормали:
где
§4. Случаи недифференцируемости непрерывной функции.
В точках §5. Производные логарифмических и показательных функций.
Основные формулы:
§6. Производные обратных тригонометрических функций.
§7. Производные гиперболических функций
1°. Определения. Выражения
2°. Свойство гиперболических функций: 1) 2) 3)
§8. Производные высших порядков
Пусть мы нашли для функции Производная третьего порядка Производная четвёртого порядка Производная n-го порядка
§9. Производные неявной функции
Если управление
§10. Дифференциал функции
Если функция
Главная часть
Положив в формуле (2)
формула (3) верна и в том случае, если Из (1) следует, что В части, для линейной функции
§11. Параметрические уравнения кривой
Пусть кривая задана параметрическими уравнениями
Задачи
1. Построить график функции:
2. Построить графики функции: 1).
3. Найти область определения вещественных значений функций: 1).
4. Доказать что limn→¥ 0.666…6 =
5. Пусть an – внутренний угол правильного n – угольника. Доказать, что limn→¥ an = p.
6. На продолжении отрезка АВ = а справа взята точка М на расстоянии ВМ=x. Найти
Найти пределы:
7.
8.
9.
10.
11.
12.
13. Капля испаряется так, что её радиус стремится к 0. Определить порядки бесконечно малых поверхности и объёма капли относительно её радиуса.
14. Определить порядки бесконечно малых: 1).
15. Доказать, что при x→0: 1) arctgmx » mx; 2)
16. Указать точку разрыва функции
17. Найти точки разрыва и построить графики функций: 1)
18. Сколько однозначных функций задано уравнением x2 + y2 = 4? Определить из них: 1) две непрерывные на отрезке
19. Построить кривые: 1) 20. Найти асимптоты кривых: 1) 21. Найти асимптоты кривых и построить кривые: 1)
Найти пределы: 22.
23. 24.
Найти производные функций:
25.
26.
27. 28. 29. 30. 31. В какой точке параболы 32. Найти длину подкасательной, поднормали, касательной и нормали кривой 33. Какие углы образуют парабола 34. На отрезке [0;p] построить график функции 35. На отрезке [-2;0] построить график функции 36. На отрезке [-1;5] построить график функции
Найти производный функции: 37. 38. 39. Написать уравнение касательной к кривой 40. 41.
42. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 и
и  ……………………...5
……………………...5 при
при 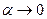 …………………………………………………………………………………..…5
…………………………………………………………………………………..…5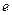 …………………………………………………………………………………..7
…………………………………………………………………………………..7 §1. Переменные величины и функции.
§1. Переменные величины и функции.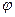 (x) и т.п. Символ f(x) или F(x) и т.п. обозначает закон соответствия переменных x и y, в частности, он может означать совокупность действий или операций, которые нужно выполнить над x, чтобы получить соответствующее значение y.
(x) и т.п. Символ f(x) или F(x) и т.п. обозначает закон соответствия переменных x и y, в частности, он может означать совокупность действий или операций, которые нужно выполнить над x, чтобы получить соответствующее значение y. > 0 найдётся зависящее от
> 0 найдётся зависящее от  - окрестности числа а.
- окрестности числа а. > 0 такое, что | f(x) - b| <
> 0 такое, что | f(x) - b| <  и
и 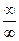
 Предел постоянной равен самой постоянной.
Предел постоянной равен самой постоянной.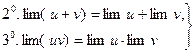 если
если  и
и 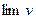 существуют.
существуют. 
 если
если 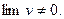
 Если для всех значений
Если для всех значений  в некоторой окрестности точки
в некоторой окрестности точки 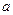 , кроме, быть может,
, кроме, быть может,  , функции
, функции  и
и  равны и одна из них имеет придел при
равны и одна из них имеет придел при  , то и вторая имеет тот же предел.
, то и вторая имеет тот же предел. и
и  при любых
при любых  .
.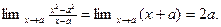
 .
. выражен в радианах, то
выражен в радианах, то
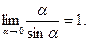
 и
и 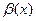 являются бесконечно малыми. Тогда:
являются бесконечно малыми. Тогда: то
то  называется бесконечно малой высшего порядка относительно
называется бесконечно малой высшего порядка относительно  .
.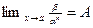 (конечен и отличен от ноля), то
(конечен и отличен от ноля), то  -го порядка относительно
-го порядка относительно 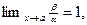 то
то  .
. Свойства эквивалентных бесконечно малых:
Свойства эквивалентных бесконечно малых: мы применяем как для обозначения эквивалентности, так и для записи приближенного равенства их достаточно малых значений.
мы применяем как для обозначения эквивалентности, так и для записи приближенного равенства их достаточно малых значений.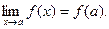
 и
и  ;
;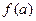 .
. , если она непрерывна в каждой точке внутри отрезка, а на его границах
, если она непрерывна в каждой точке внутри отрезка, а на его границах 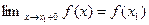 и
и  .
. , показательная
, показательная  , логарифмическая, тригонометрические и им обратные, а также их сумма, произведение, частное непрерывны при всяком
, логарифмическая, тригонометрические и им обратные, а также их сумма, произведение, частное непрерывны при всяком  слева или справа равен
слева или справа равен 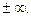
 имеет при
имеет при 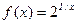 так же имеет при
так же имеет при  разрыв II рода, так как
разрыв II рода, так как  но
но 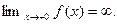
 то прямая
то прямая 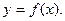
 имеет асимптоту
имеет асимптоту  имеет асимптоту y = x + 1 (и асимптоту x = 0); 2) кривая
имеет асимптоту y = x + 1 (и асимптоту x = 0); 2) кривая 
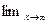 или
или  и
и  или
или  есть асимптота.
есть асимптота.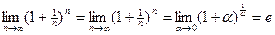
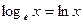

 .Определения. Производной функции
.Определения. Производной функции  в точке x называется предел
в точке x называется предел (1)
(1) (или
(или 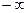 ), то будем говорить, что функция
), то будем говорить, что функция  или
или  Нахождение производной называется дифференцированием функции.
Нахождение производной называется дифференцированием функции. .Основные формулы дифференцирования.
.Основные формулы дифференцирования. 3)
3) 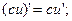
 5)
5) 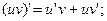
 7)
7) 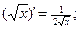
 9)
9) 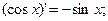
 11)
11) 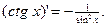
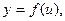 а
а  то y называется функцией от функции или сложной функцией от x. Тогда
то y называется функцией от функции или сложной функцией от x. Тогда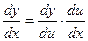 или
или 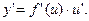 (1)
(1)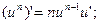 2)
2)  3)
3)  4)
4) 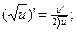
 6)
6) 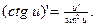
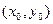 равен значению производной функции
равен значению производной функции  :
: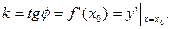 (1)
(1) называют иногда наклоном кривой в точке
называют иногда наклоном кривой в точке  Уравнение касательной к точке
Уравнение касательной к точке  на кривой:
на кривой: (2)
(2) (3)
(3) называются соответственно подкасательной и поднормалью, а длины отрезков
называются соответственно подкасательной и поднормалью, а длины отрезков  и
и  - длинами касательной и нормали.
- длинами касательной и нормали. кривой
кривой  не существует, но существует левая и правая различные производные:
не существует, но существует левая и правая различные производные:  и
и  . Из угловой точки выходят два касательных луча с наклонами
. Из угловой точки выходят два касательных луча с наклонами  и
и  .
. называется точкой возврата с вертикальной касательной, если в этой точке производная
называется точкой возврата с вертикальной касательной, если в этой точке производная  Точка перегиба с вертикальной касательной. Точка
Точка перегиба с вертикальной касательной. Точка  называется точка перегиба с вертикальной касательной, если в ней существует бесконечная производная
называется точка перегиба с вертикальной касательной, если в ней существует бесконечная производная  или
или  и
и  функция
функция 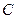 она имеет бесконечную производную. Во всех трех точках функция непрерывна, но недифференцируема.
она имеет бесконечную производную. Во всех трех точках функция непрерывна, но недифференцируема.
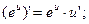


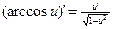 ;
;
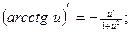
 ,
,  и их отношения называются соответственно гиперболическим синусом, косинусом, тангенсом и котангенсом и обозначаются
и их отношения называются соответственно гиперболическим синусом, косинусом, тангенсом и котангенсом и обозначаются ,
,  ,
,  ,
, 
 4)
4) 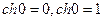
 5)
5) 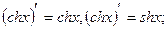
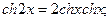 6)
6) 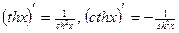
 ее производную
ее производную 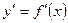 . Производная от этой производно называется производной второго порядка функции
. Производная от этой производно называется производной второго порядка функции  и обозначаются
и обозначаются  или
или  или
или  . Аналогично определяется и обозначаются
. Аналогично определяется и обозначаются

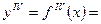


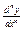
 , неразрешенное относительно
, неразрешенное относительно  , определяет
, определяет  , где
, где 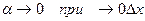 ; отсюда
; отсюда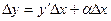 . (1)
. (1) приращения
приращения  функции, линейная относительно
функции, линейная относительно  , называется дифференциалом функции и обозначается
, называется дифференциалом функции и обозначается 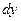
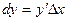 (2)
(2) , получим
, получим  , и поэтому
, и поэтому (3)
(3) , т.е. при достаточно малом
, т.е. при достаточно малом  приращение функции приближено равно ее дифференциалу.
приращение функции приближено равно ее дифференциалу.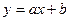 имеем:
имеем:  .
.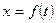 и
и  . Обозначая точками производные по параметру, найдем:
. Обозначая точками производные по параметру, найдем: .
. на отрезке [-2,5];
на отрезке [-2,5]; ; 2).
; 2).  ;
; ; 2).
; 2).  ;
; , составив разности
, составив разности  ;
;  ; …;
; …;  .
. .
. .
. .
. .
. .
. .
. .
. ; 2).sin2x-sinx относительно бесконечно малой x.
; 2).sin2x-sinx относительно бесконечно малой x. .
.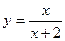 , найти limn→-2-0 y, limx→-2+0 y,limx→¥ и построить график по точкам x = -6, -4, -3, -1, 0, 2.
, найти limn→-2-0 y, limx→-2+0 y,limx→¥ и построить график по точкам x = -6, -4, -3, -1, 0, 2. ; 2)
; 2)  .
. ; 2) ту из них, отрицательна на отрезке
; 2) ту из них, отрицательна на отрезке  и положительна для всех остальных допустимых значений x. Построить график и указать разрывы последней функции.
и положительна для всех остальных допустимых значений x. Построить график и указать разрывы последней функции. ; 2)
; 2)  и параболы, к которым эти кривые асимптотически приближаются.
и параболы, к которым эти кривые асимптотически приближаются. ; 2)
; 2)  и построить кривые по точкам
и построить кривые по точкам 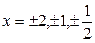 .
. ; 2)
; 2) 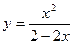 .
. .
. (положить cos22x = a).
(положить cos22x = a). .
. ;
; ; найти
; найти  ;
; ; найти
; найти  ,
,  и
и  ;
; ;
; ;
; ; найти
; найти 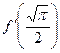 ;
; нужно провести касательную, чтобы она была перпендикулярна к биссектрисе первого координатного угла?
нужно провести касательную, чтобы она была перпендикулярна к биссектрисе первого координатного угла?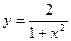 в точке x = 1.
в точке x = 1. с её хордой, абсциссы концов которой равны 2 и 4?
с её хордой, абсциссы концов которой равны 2 и 4?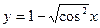 и написать уравнения касательных к кривой в угловой точке.
и написать уравнения касательных к кривой в угловой точке. и написать уравнения касательных к кривой в точке x = -1.
и написать уравнения касательных к кривой в точке x = -1.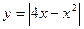 и написать уравнения касательных в угловой точке x = 0 и найти угол между ними.
и написать уравнения касательных в угловой точке x = 0 и найти угол между ними. ;
; ; найти
; найти  ;
; в точке пересечения её с осью Оу. Построить кривую, касательную и асимптоту кривой;
в точке пересечения её с осью Оу. Построить кривую, касательную и асимптоту кривой; ;
; ;
; ; найти
; найти