
|
|
Алгоритм построчного сканирования, использующий z-буфер.Одним из простейших алгоритмов построчного сканирования, который решает задачу удаления невидимых поверхностей, является специальный случай алгоритма z-буфера. Используемое в этом алгоритме окно визуализации имеет высоту в одну сканирующую строку и ширину во весь экран. Как для буфера кадра, так для z- буфера требуется память высотой в 1 бит, шириной в горизонтальное разрешение окна и глубиной в зависимости от требуемой точности. Обеспечиваемая точность по глубине зависит от диапазона значений, которые может принимать z. Концептуально этот алгоритм достаточно прост. Для каждой сканирующей строки буфер кадра инициализируется с фоновым значением интенсивности, а z- буфер – с минимальным значением z. Затем определяется пересечение сканирующей строки с двумерной проекцией каждого многоугольника сцены, если они существуют. При рассмотрении каждого пиксела на сканирующей строке в интервале между концами пар его глубина сравнивается с глубиной, содержащейся в соответствующем элементе z-буфера. Если глубина этого пиксела больше глубины из z-буфера, то рассматриваемый отрезок будет текущим видимым отрезком. И следовательно, атрибуты многоугольника, соответствующего данному отрезку, заносятся в буфер кадра в позиции данного пиксела; соответственно корректируется и z-буфер в этой позиции. После обработки всех многоугольников сцены буфер кадра размером в одну сканирующую строку содержит решение задачи удаления невидимых поверхностей для данной сканирующей строки. Он выводится на экран дисплея в порядке, определяемом растровым сканированием, то есть слева направо. В этом алгоритме можно использовать методы устранения ступенчатости, основывающиеся как на пре-, так и на постфильтрации. Однако практически сравнение каждого многоугольника с каждой сканирующей строкой оказывается неэффективным. Поэтому используется некоторая разновидность списка упорядоченных ребер. В частности, для повышения эффективности этого алгоритма применяются групповая сортировка по оси у, список активных многоугольников и список активных ребер. С использованием этих методов алгоритм построчного сканирования с z-буфером формулируется следующим образом: Подготовка информации: - Для каждого многоугольника определить самую верхнюю сканирующую строку, которую он пересекает. - Занести многоугольник в группу у, соответствующую этой сканирующей строке. - Запомнить для каждого многоугольника, например в связном списке, как минимум следующую информацию: Решение задачи удаления невидимых поверхностей: - Инициализировать буфер кадра дисплея. - Для каждой сканирующей строки: 1. Инициализировать буфер кадра размером с одну сканирующую строку, заполнив его фоновым значением. 2. Инициализировать z-буфер размером с одну сканирующую строку значением 3. Проверить появление в группе у сканирующей строки новых многоугольников. Добавить все новые многоугольники к списку активных многоугольников. 4. Проверить появление новых многоугольников в списке активных многоугольников. Добавить все пары ребер новых многоугольников к списку активных ребер. 5. Если какой-нибудь элемент из пары ребер многоугольника удаляется из списка активных ребер, то надо определить, сохранился ли соответствующий многоугольник в списке активных многоугольников. Если сохранился, то укомплектовать пару активных ребер этого многоугольника в списке активных ребер. В противном случае удалить и второй элемент пары ребер из списка активных ребер. Алгоритм Робертса
Алгоритм Робертса представляет собой метод, работающий в объектном пространстве. Алгоритм прежде всего удаляет из каждого тела те ребра или грани, которые экранируются самим телом. Затем каждое из видимых ребер каждого тела сравнивается с каждым из оставшихся тел для определения того, какая его часть или части, если таковые есть, экранируются этими телами. Поэтому вычислительная трудоемкость алгоритма Робертса растет теоретически как квадрат числа объектов. Математические методы, используемые в этом алгоритме, просты и точны. Этот алгоритм иллюстрирует некоторые важные концепции, используемые при создании реалистичных изображений (методы Гуро, Фонга), а также используется в системах геометрического моделирования при визуализации сцен для отбрасывания нелицевых граней. Некоторые реализации алгоритма, использующие предварительную приоритетную сортировку вдоль оси z и простые габаритные или минимаксные тесты, демонстрируют почти линейную зависимость от числа объектов. В алгоритме Робертса требуется, чтобы все изображаемые тела или объекты были выпуклыми. Невыпуклые тела должны быть разбиты на выпуклые части. В этом алгоритме выпуклое многогранное тело с плоскими гранями должно представляться набором пересекающихся плоскостей. Уравнение произвольной плоскости в трехмерном пространстве имеет вид: ax+by+cz+d=0. В матричной форме этот результат выглядит так: [x y z 1]
или [x y z 1][P]T=0
Где каждый столбец содержит коэффициенты одной плоскости. Любая точка пространства представима в однородных координатах вектором [S]=[x y z 1 ]
a×x1 + b×y1 + c×z1 = -1 a×x2 + b×y2 + c×z2 = -1 a×x3 + b×y3 + c×z3 = -1 В матричной форме это выглядит так:
Или [X]*[C]=[D] Решение этого уравнения дает значения коэффициентов уравнения плоскости:
Другой способ используется, если известен вектор нормали к плоскости, т.е. n = ai + bj + ck Где i,j,k - единичные векторы осей x, y, z соответственно. Тогда уравнение плоскости принимает вид ax + by + cz + d = 0 Величина d вычисляется с помощью произвольной точки на плоскости. В частности, если компоненты этой точки на плоскости (x1, y1, z1), то: d = -(ax1 + by1 + cz1). Объем вычислений в алгоритмах удаления невидимых линий или поверхностей растет с увеличением числа многоугольников с более чем тремя сторонами. Эти многоугольники могут быть как невыпуклыми, так и неплоскими. Метод, предложенный Ньюэлом, позволяет найти как точное решение для уравнений плоскостей, содержащих плоские многоугольники, так и "наилучшее" приближение для неплоских многоугольников. Этот метод эквивалентен определению нормали в каждой вершине многоугольника посредством векторного произведения прилежащих ребер и усреднения результатов. Если a, b, c, d - коэффициенты уравнения плоскости, то:
Перед началом работы алгоритма удаления невидимых линий или поверхностей для получения желаемого вида сцены применяется трехмерное видовое преобразование. Матрицы тел для объектов преобразованной сцены можно получить или преобразованием исходных матриц тел или вычислением новых матриц тел, используя преобразованные вершины или точки. Если [B] - матрица однородных координат, представляющая исходные вершины тела, а [T] - матрица размером 4*4 видового преобразования (матрица проектирования), то преобразованные вершины таковы: [BT] = [B][T] где [BT] - преобразованная матрица вершин. Использования уравнения (3.11) позволяет получить уравнения исходных плоскостей, ограничивающих тело: [B][V] = [D] (3.12) где [V] - матрица тела, а [D] в правой части - нулевая матрица. Аналогично уравнения преобразованных плоскостей задаются следующим образом: [BT][VT] = [D] (3.13) где [BT] - преобразованная матрица тела. Приравнивая левые части уравнения (3.12) и (3.13), получаем: [BT][VT] =[B][V] Подставляя уравнение (3.12), сокращая на [B] и умножая слева на [T]-1, имеем
Итак, преобразованная матрица тела получается умножением исходной матрицы тела слева на обратную матрицу видового преобразования.
В алгоритме Робертса принято, что если скалярное произведение точки на матрицу тела (фактически на вектора нормалей плоскостей, образующих тело) отрицательно, то точка лежит вне этого тела и наоборот. Например, если зритель находится в бесконечности на положительной полуоси z, то его взгляд направлен в сторону отрицательной полуоси z. В однородных координатах вектор такого направления равен: [E]=[0 0 -1 0], который служит образом точки, лежащей в бесконечности на отрицательной полуоси z. Фактически [E] представляет любую точку, лежащую на плоскости z=-¥. Поэтому, если скалярное произведение [E] на столбец, соответствующий какой-нибудь плоскости в матрице тела, отрицательно, то [E] лежит по отрицательную сторону этой плоскости. Следовательно, эти плоскости невидимы из любой точки наблюдения z=¥, а пробная точка на z=-¥ экранируется самим телом. Такие плоскости называют нелицевыми. Следовательно, условие: [E]×[V]<0 является условием того, что плоскости нелицевые, а их грани – задние. Иначе этот способ называют отбрасыванием задних плоскостей.
Контрольные вопросы 1. Для чего применяются алгоритмы удаления невидимых линий и поверхностей? 2. Какие функции используются в алгоритмах удаления невидимых линий и поверхностей? 3. Что такое "Функция стратегии"? 4. Классификация алгоритмов удаления невидимых поверхностей. 5. Преимущества алгоритма, использующего z-буфер. 6. Основные шаги в алгоритме, использующего z-буфер. 7. Алгоритм построчного сканирования. 8. Основные шаги алгоритма построчного сканирования. Модели закраски.
Если при построении полигональной поверхности для каждой грани используется по одной нормали, то модель освещения создает изображение, состоящее из отдельных многоугольников. Такой метод называется однотонной закраской.
Однотонная закраска многоугольников и интерполяционное закрашивание. Методом интерполяционного закрашивания можно получить сглаженное изображение. Для того чтобы изобразить объект методом построчного сканирования, нужно в соответствии с моделью освещения рассчитать интенсивность каждого пиксела вдоль сканирующей строки. Нормали к поверхности аппроксимируются в вершинах многоугольников. Однако сканирующая строка не обязательно проходит
Рассмотрим, например, участок полигональной поверхности на рис.2. Значение интенсивности в точке Р определяется линейной интерполяцией интенсивности в точках Q и R. Для получения интенсивности в точке Q - пересечении ребра многоугольника со сканирующей строкой - нужно линейной интерполяцией интенсивностей А и В найти IQ = uIA + (1 - u)IB; 0<=u<=1 ,где u = AQ/AB. Аналогично для получения интенсивности R линейно интерполируются интенсивности в вершинах В и С, т. е. IR = wIB + (1 - w)Ic 0 <= w <= 1 ,где w = BR/BC. Наконец, линейной интерполяцией по строке между Q и R находится интенсивность Р, т.е. IP = tIQ + (1 - t)IR; 0<=w<=1 ,где t = QP/QR. Значения интенсивности вдоль сканирующей строки можно вычислять инкрементально. Для двух пикселов в t1 и t2 на сканирующей строке IP2 = t2IQ + (1 - t2)IR IP1 = tlIQ + (1 - t1)IR Вычитая, получим, что вдоль строки IP2 = IP1 + (IQ - IR)(t2 - t1) = IP1 + На рис. показан результат применения интерполяционной закраски к полигональной аппроксимации лица, изображенного на рис.1, слева. Видно, что качество изображения намного улучшилось, но при внимательном рассмотрении на рис.1, справа, заметно проявление эффекта полос Маха, например на скулах, вокруг глаз и на подбородке. Это происходит потому, что такой метод интерполяции обеспечивает лишь непрерывность значений интенсивности вдоль границ многоугольников, но не обеспечивает непрерывности изменения интенсивности. Обратите внимание также на то, что контуры лица, например глаз и носа, - многоугольники. При закраске по Гуро(Guraud) с вершинами связываются нормали, которые получаются в результате усреднения нормалей многоугольников, пересекающихся в этой вершине, т.е. для четырёхугольников, например:
где
Рис Эффекты закраски Гуро. Проблема метода Гуро иллюстрируется на рис., а. Если нормали к вершинам В, С, D вычислить усреднением нормалей к многоугольникам, то они будут одинаково ориентированы, т. е. интенсивность в этих точках будет равной. При линейной интерполяции от В до D значение интенсивности получится постоянным, и поверхность на данном участке будет выглядеть плоской. Для изображения плавного перехода в В, С и D необходимы дополнительные многоугольники (рис. b). Если же нужно сохранить резкие складки, то для предотвращения сглаживания требуется выборочное усреднение нормалей к поверхности. В примере, показанном на рис. с, nB1 вычисляется только для одной грани справа от В, аналогично получается nD1 и nD2. В то же время nC вычисляется как среднее для граней слева и справа от С. В этом случае в В и D получается острое ребро, а в С - плавный переход. Закраска Фонга требует больших вычислительных затрат, однако она позволяет разрешить многие проблемы метода Гуро. При закраске Гуро вдоль сканирующей строки интерполируется значение интенсивности, а при закраске Фонга - вектор нормали. Затем он используется в модели освещения для вычисления интенсивности пиксела. При этом достигается лучшая локальная аппроксимация кривизны поверхности и, следовательно, получается более реалистичное изображение. В частности, правдоподобнее выглядят зеркальные блики. При закраске Фонга аппроксимация кривизны поверхности производится сначала в вершинах многоугольников путем аппроксимации нормали в вершине. После этого билинейной интерполяцией вычисляется нормаль в каждом пикселе. Например, снова обращаясь к рис. 11.10, получаем нормаль в Q линейной интерполяцией между A и B, в R - между B и C и, наконец, в P - между Q и R. Таким образом:
где u=AQ/AB, w=BR/BC, t=QP/QR. Нормаль вдоль сканирующей строки опять можно выразить через приращение, т. е.
где индексы 1 и 2 указывают на расположение пискелов на строке.
Рис. Интерполирование нормалей вдоль ребра полигональной сети. Рассмотрим отдельный многоугольник полигональной сети, представленный на рис. С каждой вершиной можно связать нормаль, которая формируется усреднением нормалей к граням, пересекающимся в этой вершине. Далее, с помощью билинейной интерполяции, можно интерполировать нормали по всей внутренней области многоугольника. Рассмотрим рис. Векторы нормалей в вершинах A и B используются для интерполяции вдоль ребра, связывающего эти две вершины:
Аналогичную процедуру можно выполнить и для других рёбер многоугольника. Затем можно вычислить нормаль в любой точке внутренней области этого многоугольника, зная распределение нормалей на его рёбрах:
Получив вектор нормали в определённой точке, можно выполнить все необходимые вычисления, определяемые используемой моделью отражения. Обычно этот процесс реализуется вместе с растровым преобразованием многоугольника, в результате чего отрезок между точками C и D проецируется на участок строки развёртки в буфере кадра. Хотя метод Фонга устраняет большинство недостатков метода Гуро, он тоже основывается на линейной интерполяции. Поэтому в местах разрыва первой производной интенсивности заметен эффект полос Маха, хотя и не такой сильный, как при закраске Гуро. Однако, иногда этот эффект проявляется сильнее у метода Фонга, например для сфер. Кроме того, оба метода могут привести к ошибкам при изображении невыпуклых многоугольников. Контрольные вопросы 1. Как выполняется закраска Гуро? 2. Причины появления эффекта полос Маха при закраске Гуро. 3. Вычисление нормали при закраске Гуро. 4. Вычисление интенсивности в закраске Гуро. Системы цветов
Система цветов RGB Монитор компьютера создает цвет непосредственно излучением света и, использует схему цветов RGB. Если с близкого расстояния посмотреть на экран монитора, то можно заметить, что он состоит из мельчайших точек красного, зелёного и синего цветов. Компьютер может управлять количеством света, излучаемого через любую окрашенную точку и, комбинируя различные сочетания любых цветов, может создать любой цвет. Будучи определена природой компьютерных мониторов, схема RGB является самой популярной и распространённой, но у неё есть недостаток: компьютерные рисунки не всегда должны присутствовать только на мониторе, иногда их приходится распечатывать, тогда необходимо использовать другую систему цветов - CMYK. Система цветов CMYK Данная система была широко известна задолго до того, как компьютеры стали использоваться для создания графических изображений. Для разделения цветов изображения на цвета CMYK применяют компьютеры, а для полиграфии разработаны их специальные модели. Преобразование цветов из системы RGB в систему CMYK сталкивается с рядом проблем. Основная сложность заключается в том, что в разных системах цвета могут меняться. У этих систем различна сама природа получения цветов и то, что мы видим на экране мониторов никогда нельзя точно повторить при печати. В настоящее время существуют программы, которые позволяет работать непосредственно в цветах CMYK. Программы векторной графики уже надёжно обладают этой способностью, а программы растровой графики лишь в последнее время стали предоставлять пользователям средства работы с цветами CMYK и точного управления тем, как рисунок будет выглядеть при печати. Системы цветов HSB и HSL Системы цветов HSB и HSL базируется на ограничениях, накладываемых аппаратным обеспечением. В системе HSB описание цвета представляется в виде тона, насыщенности и яркости. В другой системе HSL задаётся тон, насыщенность и освещённость. Тон представляет собой конкретный оттенок цвета. Насыщенность цвета характеризует его относительную интенсивность или частоту. Яркость или освещённость показывают величину чёрного оттенка добавленного к цвету, что делает его более тёмным. Система HSB хорошо согласовывается с моделью восприятия цвета человеком, то есть он является эквивалентом длины волны света. Насыщенность - интенсивность волны, а яркость - общее количество света. Недостатком этой системы является то, что для работы на мониторах компьютера её необходимо преобразовать в систему RGB, а для четырехцветной печати в систему CMYK. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 число сканирующих строк, которые пересекаются этим многоугольником; список ребер многоугольника; коэффициенты
число сканирующих строк, которые пересекаются этим многоугольником; список ребер многоугольника; коэффициенты  уравнения плоскости многоугольника; визуальные атрибуты многоугольника.
уравнения плоскости многоугольника; визуальные атрибуты многоугольника. .
. =0
=0
 Поэтому любое выпуклое твердое тело можно выразить матрицей тела, состоящей из коэффициентов уравнений плоскостей, т.е.
Поэтому любое выпуклое твердое тело можно выразить матрицей тела, состоящей из коэффициентов уравнений плоскостей, т.е. Более того, если точка [S] лежит на плоскости, то. Если же [S] не лежит на плоскости, то знак этого скалярного произведения показывает, по какую сторону от плоскости расположена точка. В алгоритме Робертса предполагается, что точки, лежащие внутри тела, дают положительное скалярное произведение. Уравнение плоскости содержит четыре неизвестных коэффициента, его можно нормировать так, чтобы d=1. Следовательно, трех неколлинеарных точек (x1, y1,z1), (x2, y2, z2), (x3, y3, z3) достаточно для определения плоскости. Подставим координаты этих точек в нормированное уравнение (3.12) дает:
Более того, если точка [S] лежит на плоскости, то. Если же [S] не лежит на плоскости, то знак этого скалярного произведения показывает, по какую сторону от плоскости расположена точка. В алгоритме Робертса предполагается, что точки, лежащие внутри тела, дают положительное скалярное произведение. Уравнение плоскости содержит четыре неизвестных коэффициента, его можно нормировать так, чтобы d=1. Следовательно, трех неколлинеарных точек (x1, y1,z1), (x2, y2, z2), (x3, y3, z3) достаточно для определения плоскости. Подставим координаты этих точек в нормированное уравнение (3.12) дает:





 через вершины многоугольника (При закраске Гуро сначала определяется интенсивность вершин многоугольника, а затем с помощью билинейной интерполяции вычисляется интенсивность каждого пиксела на сканирующей строке.
через вершины многоугольника (При закраске Гуро сначала определяется интенсивность вершин многоугольника, а затем с помощью билинейной интерполяции вычисляется интенсивность каждого пиксела на сканирующей строке. I
I  ,
, - нормали к граням четырёхугольников, смежных с вершиной
- нормали к граням четырёхугольников, смежных с вершиной




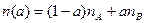

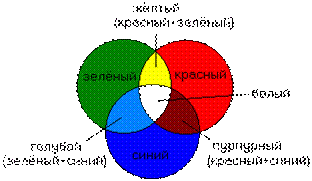 Аддитивный цвет получается при соединении света разных цветов. В этой схеме отсутствие всех цветов представляет собой чёрный цвет, а присутствие всех цветов - белый. Схема аддитивных цветов работает с излучаемым светом, например, монитор компьютера.
Аддитивный цвет получается при соединении света разных цветов. В этой схеме отсутствие всех цветов представляет собой чёрный цвет, а присутствие всех цветов - белый. Схема аддитивных цветов работает с излучаемым светом, например, монитор компьютера. В схеме субтрактивных цветов происходит обратный процесс. Здесь получается какой-либо цвет при вычитании других цветов из общего луча света. В этой схеме белый цвет появляется в результате отсутствия всех цветов, тогда как их присутствие даёт чёрный цвет. Схема субтрактивных цветов работает с отражённым светом.
В схеме субтрактивных цветов происходит обратный процесс. Здесь получается какой-либо цвет при вычитании других цветов из общего луча света. В этой схеме белый цвет появляется в результате отсутствия всех цветов, тогда как их присутствие даёт чёрный цвет. Схема субтрактивных цветов работает с отражённым светом.