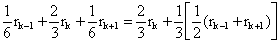Применение в компьютерной графике

Благодаря простоте задания и возможности удобно манипулировать формой, кривые Безье нашли широкое применение в компьютерной графике для моделирования гладких линий. Поскольку кривая полностью определяется своей выпуклой оболочкой из опорных точек, последние могут быть отображены и использоваться для наглядного управления формой линии. Кроме того аффинные преобразования кривой (перенос, масштабирование, вращение) также легко могут быть осуществлены путём применения трансформаций к опорным точкам. Наличие выпуклой оболочки значительно облегчает задачу о точках пересечения кривых Безье: если не пересекаются выпуклые оболочки, то не пересекаются и сами кривые.

Наибольшее значение имеют кубические кривые Безье. Кривые высших степеней при обработке требуют большего объёма вычислений и для практических целей используются реже. Для построения сложных по форме линий отдельные кривые Безье могут быть последовательно соединены друг с другом в сплайн Безье. Для того, чтобы обеспечить гладкость линии в месте соединения двух кривых, смежные опорные точки обеих кривых должны лежать на одной линии. В программах векторной графики наподобие Adobe Illustrator или Inkscape подобные фрагменты известны под названием «путей» (path).

Контрольные вопросы

1. Как определяется параметрическая кубическая кривая⁹

2. Укажите свойства параметрической кубической кривой

3. Напишите уравнение кривой в форме Фергюсона

4. Каким образом можно управлять формой кривой в форме Фергюсона?

5. Напишите уравнение кривой в форме Безье

6. Через какие опорные точки проходит кривая Безье?

7. Напишите базисну матрицу кубической кривой Безье

8. Как используются кривые Безье в компьютерной графике?

Представление кривых. Сплайны

Можно строить достаточно гладкие кривые и поверхности с использованием полиномов. Допустим, что мы хотим построить поверхность в виде графика функции z=z(x, y). Линия y=const на этой поверхности будет представлена линией z=z(x), она будет проходить через последовательность точек (x₀,z₀), (x_i,z_i), ..., (x_n,z_n),

x₀<x₁<...<x_n.

Наша цель - провести через эти точки составную кривую f(x), имеющую следующие свойства:

- на каждом подынтервале x_i-1<= x<= x_i, i=1,2,.., n, функция f(x) является кубическим полиномом.

- её первые и вторые производные непрерывны в узлах

Полученная гладкая кривая называется кубическим сплайном. Термин сплайн возник по аналогии: это название чертежного инструмента - тонкой металлической линейки, которая может изгибаться так, чтобы проходить через заданные точки. Физически такая кривая минимизирует энергию внутренних напряжений. Математически - имеет минимальную среднеквадратичную кривизну, т.е. она наиболее гладкая. Сплайны имеют много приложений в конструировании криволинейных форм. Однако они имеют и некоторые ограничения:

- локальное изменение влечет за собой вычисление заново всего сплайна;

- могут возникать проблемы при аппроксимации прямой, имеющей разрывы вторых производных (например, сопряжения прямой линии и дуги окружности);

- с точки зрения эстетики не всегда приемлемы, т.к. кривизна поверхности, сконструированной с помощью сплайнов изменяется иногда неравномерно, что приводит к искажениям (например, причудливые искажения предметов, отраженных от кузова автомобиля).

Первое ограничение можно устранить с помощью В-сплайна.

В-сплайн

Общая форма полученной в результате кривой:

На этом рисунке сплайн продолжен от его конечных точек x_i-4, x_i прямыми линиями, идущими вдоль оси X. Получается кубический сплайн на любом числе отрезков, который не равен 0 на четырех из них. Такая функция называется В-сплайном (или фундаментальным сплайном). Про него говорят, что он имеет минимальный носитель (носитель - это число отрезков, на которых сплайн отличен от 0). Кубический сплайн полностью определяется множеством узлов, на которых он определен, и только одной заданной величиной. В более общем виде В-сплайн M_mi(x) порядка m (или степени m-1) на данном множестве везде равен 0, кроме m последоваельных отрезков x_i-m< x < x_i. Принято фиксировать амплитуду В-сплайна некоторым стандартным образом.

Часто удобно для вычислений использовать нормализованный В-сплайн N_mi(x), связанный с M_mi(x) соотношением:

N_mi(x)=(x_i - x_i-m)M_mi(x).

Любой кубический сплайн на множестве узлов 0,1, 2, .., n может быть выражен через кубические В-сплайны в виде:

где с_i скалярные коэффициенты. Если имеется множество векторов r₀, r₁, …, r_n , то можно использовать их:

Т.к. имеется (n+1) векторных коэффициентов, то необходим набор из (n+1) В-сплайнов. Последняя формула, для , является уравнением кривой, образованной кубическими В-сплайнами.

Свойства

Некоторые простейшие свойства следуют из тождества:

При u=0 следует:

Из этого следует, что если r₀, r₁, .., r_n - вершины некоторой замкнутой ломанной, то кривая, построенная на основе В сплайна, начинается в r₀ и ее касательная в этой точке имеет направление (r₁ - r₀). Аналогичное утверждение верно и для другого конца. Главное преимущество этого сплайна заключается в том, что изменение одной из вершин влечет за собой изменение только четырех отрезков кривой. Далее, мы также можем построить кривую, аппроксимирующую ломанную с любым желаемым числом сторон. Отрезок сплайна всегда лежит в выпуклой оболочке:

Важным следствием этой выпуклой оболочки является вырождение ее в прямую линию, если 4 последовательные вершины ломанной коллинеарны, значит соответствующий сегмент кривой должен быть прямолинейным. Имеются ещё 2 полезных факта:

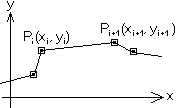
- кривая проходит вблизи средней точки каждой стороны, за исключением 1-ой и последней точками;

- при k=2, .., n-2 кривая проходит через точки:

Эти точки, как показано на рисунке, лежат на 1/3 расстояния от r_k на прямой, соединяющей r_k с серединой отрезка между r_k-1 и r_k+1.

Рассмотрим построение кубического сплайна. Пусть нам даны две соседние точки через которые проведём кубический полином, но у полинома - 4 коэффициента, следовательно нужно ещё два дополнительных условия или точки. Для этого прихватим ещё две соседние точки.

Чем более плавной мы хотим видеть линию, тем сложнее пройти точно через точки.

Если в формуле x = q³, то достаточно плавности 3. Гладкость диктуется физическими задачами.

Эта линия в каждой точке имеет систему:

	x(t) y(t)	если t = 0 =< Pi t = 1 =< Pi+1	t - параметр по которому перебегаем от точки к точке.
	x(t) = ((a3 + a2)t + a1)t + a0 y(t) = ((b3 + b2)t + b1)t + b0

a₃ = (-x_i-1+ 3x_i - 3x_i+1 + x_i+2)/6

a₂ = (x_i-1 - 2x_i+ x_i+1)/2

a₁ = (-x_i-1 + x_i+1)/2

a₀ = (x_i-1 + 4x_i+ x_i+1)/6

Точки b₃ - b₀ расписывают также, но вместо x подставляют у.

Между P_i и P_i+1 точки а и b не меняются.

Есди после последней точки указать первую точку, то система замкнёт контур.

Достоинства В - сплайна: между точками коэффициенты постоянны; локаьное изменение не влечет за собой вычисление заново всего сплайна.

Недостатки: могут возникатьпроблемы при аппроксимации прямой, имеющей разрывы вторых производных (например, сопряжения прямой линии и дуги окружности); с точки зрения эстетики не всегда приемлемы, т.к. кривизна поверхности, сконструированной с помощью сплайнов изменяется иногда неравномерно, что приводит к искажениям (например, причудливые искажения предметов, отраженных от кузова автомобиля).

Следствия

1. Кривые отходят от точек.

x_i: x(0) = a₀ = (x_i-1+ 4x_i + x_i+1)/6

x_i+1: x(1) = a₃ + a₂ + a₁ + a₀ = (x_i + 4x_i+1 + x_i+2)/6

точки усредняют своё влияние.

2. Изменение одной вершины ведёт к изменению только четырёх соседних отрезков.

3. Геометрическая интерпретация В - сплайна: так как сумма коэффициентов = 1, а коэффициенты положительны, то мы получаем средне взвешенную точку для четырёх соседей, то есть первоначальный отрезок будет находиться внутри выпуклой сплайновой оболочки.

Формула расчёта:

1/6х_i-1 + 2/3x_i + 1/6x_i+1 = 2/3x_i + 1/3[1/2(x_i-1 + x_i+1)]

4. Кратность вершины усиливает её притяжение.

В острые углы линия не успевает забегать. В этом случае увеличивают кратность вершины. Порядок сплайна влияет на конфигурацию - увеличение порядка ведёт к большему спрямлению.

Контрольные вопросы

1. Дайте определение кубического сплайна

2. Математический и физический смысл сплайна

3. Недостатки сплайна

4. Напишите уравнение кривой в форме В-сплайнов

5. Для чего применяется нормализованный В-сплайн

6. Свойства В-сплайна

7. Укажите условия применения разных форм представления кривой.

8. Укажите интерпретацию геометрических матриц Безье и В-сплайнов.

Не нашли, что искали? Воспользуйтесь поиском по сайту: