
|
|
Преобразования в пространстве.Поступая аналогично тому, как это было сделано в размерности два, заменим координатную тройку (x, у, z), задающую точку в пространстве, на четверку чисел (x, у, z, 1) или, более общо, на четверку
Каждая точка пространства (кроме начальной точки О) может быть задана четверкой одновременно не равных нулю чисел; эта четверка чисел определена однозначно с точностью до общего множителя. Предложенный переход к новому способу задания точек дает возможность воспользоваться матричной записью и в более сложных, трехмерных задачах. Любое аффинное преобразование в трехмерном пространстве может быть представлено в виде суперпозиции вращений, растяжений, отражений и переносов. Поэтому вполне уместно сначала подробно описать матрицы именно этих преобразований (ясно, что в данном случае порядок матриц должен быть равен четырем).
А. Матрицы вращения в пространстве. Матрица вращения вокруг оси абсцисс на угол φ:
Матрица вращения вокруг оси ординат на угол ψ:
Матрица вращения вокруг оси аппликат на угол χ:
Замечание. Полезно обратить внимание на место знака "-" в каждой из mpex приведенных матриц. Б. Матрица растяжения (сжатия): где α > 0 - коэффициент растяжения (сжатия) вдоль оси абсцисс; β > 0 - коэффициент растяжения (сжатия) вдоль оси ординат; γ > 0 - коэффициент растяжения (сжатия) вдоль оси аппликат.
В. Матрицы отражения. Матрица отражения относительно плоскости xу:
Матрица отражения относительно плоскости уz:
Матрица отражения относительно плоскости zx:
Г. Матрица переноса (здесь (λ, μ, v) - вектор переноса):
Замечание. Как и в двумерном случае, все выписанные матрицы невырождены.
Контрольные вопросы 1. Назовите элементарные геометрические преобразования двумерных объектов. 2. Сформулируйте определение переноса. 3. Дайте определение масштабирования. 4. Как вычисляются координаты точки при повороте? 5. Для чего вводятся однородные координаты? 6. Приведите определение однородных координат. 7. Напишите матрицу переноса в однородных координатах. 8. Напишите матрицу масштабирования в однородных координатах. 9. Напишите матрицу поворота в однородных координатах. 10. Как определяется композиция геометрических преобразований? 11. Напишите матрицу трехмерного переноса. 12. Напишите матрицу трехмерного масштабирования. 13. Напишите матрицу трехмерного поворота вокруг оси z. 14. Как интерпретируются обратные матрицы элементарных геометрических преобразований? 15. Как соотносятся геометрические преобразования объектов и изменение системы координат? 16. Сформулируйте правило перехода от системы координат i к системе координат j. Виды проектирования
Изображение объектов на картинной плоскости связано с еще одной геометрической операцией - проектированием при помощи пучка прямых. В компьютерной графике используется несколько различных видов проектирования (иногда называемого также проецированием). Наиболее употребимые на практике виды проектирования: параллельное и центральное. Проецирование в общем случае - отображение точек, заданных в системе координат размерностью N, в точки в системе с меньшей размерностью. При отображении трехмерных изображений на дисплей три измерения отображаются в два. Проецирование выполняется с помощью прямолинейных проекторов (проецирующих лучей), идущих из центра проекции через каждую точку объекта до пересечения с картинной поверхностью (поверхностью проекции). Далее рассматриваются только плоские проекции, при которых поверхность проекции - плоскость в трехмерном пространстве. По расположению центра проекции относительно плоскости проекции различаются центральная и параллельные проекции. Для получения проекции объекта на картинную плоскость необходимо провести через каждую его точку прямую из заданного проектирующего пучка (собственного или несобственного) и затем найти координаты точки пересечения этой прямой с плоскостью изображения. В случае центрального проектирования все прямые исходят из одной точки - центра собственного пучка. При параллельном проектировании центр (несобственного) пучка считается лежащим в бесконечности.
Каждый из этих двух основных классов разбивается на несколько подклассов в зависимости от взаимного расположения картинной плоскости и координатных осей. Некоторое представление о видах проектирования могут дать приводимые ниже схемы.
Замечание.Использование для описания преобразований проектирования однородных координат и матриц четвертого порядка позволяет упростить изложение и зримо облегчает решение задач геометрического моделирования.
Матрица проектирования вдоль оси X на плоскость YZ имеет вид:
В случае, если плоскость проектирования параллельна координатной плоскости необходимо умножить матрицу [Рх] на матрицу сдвига. В результате получаем
Аналогично записываются матрицы проектирования вдоль двух других координатных осей:
Замечание. Все три полученные матрицы проектирования вырожденны.
При аксонометрической проекции проектирующие прямые перпендикулярны картинной плоскости. В соответствии со взаимным расположением плоскости проектирования и координатных осей различают три вида проекций: - триметрию - нормальный вектор картинной плоскости образует с ортами координатных осей попарно различные углы; - диметрию - два угла между нормалью картинной плоскости и координатными осями равны; - изометрию - все три угла между нормалью картинной плоскости и координатными осями равны.
Каждый из трех видов указанных проекций получается комбинацией поворотов, за которой следует параллельное проектирование. Наиболее широко, особенно, в САПР используются ортогональные проекции (виды). Вид - ортогональная проекция обращенной к наблюдателю видимой части поверхности предмета, расположенного между наблюдателем и плоскостью чертежа. В техническом черчении за основные плоскости проекций принимают шесть граней куба.
1. Вид спереди, главный вид, фронтальная проекция, (на заднюю грань V), 2. Вид сверху, план, горизонтальная проекция, (на нижнюю грань H), 3. Вид слева, профильная проекция, (на правую грань W), 4. Вид справа (на левую грань), 5. Вид снизу (на верхнюю грань), 6. Вид сзади (на переднюю грань). Очевидно, что при ортогональной проекции не происходит изменения ни углов, ни масштабов. При изометрических проекциях укорачивания вдоль всех координатных осей одинаковы, поэтому можно производить измерения вдоль направлений осей с одним и тем же масштабом (отсюда и название изометрия). На рис. приведена (аксонометрическая прямоугольная) изометрическая проекция куба со стороной A. При этой проекции плоскость проецирования наклонена ко всем главным координатным осям под одинаковым углом. Стандартом регламентируется коэффициент сжатия, равный 0.82, а также расположение и взаимные углы главных координатных осей, равные 120 как это показано в левом верхнем углу рис. . Обычно сжатие не делается.
При диметрической проекции две из трех осей сокращены одинаково, т.е. из трех углов между нормалью к плоскости проекции и главными координатными осями два угла одинаковы. На рис. приведена (аксонометрическая прямоугольная) диметрическая проекция куба со стороной A. Там же показаны регламентируемые расположение осей и коэффициенты сжатия. Обычно вместо коэффициента сжатия 0.94 используется 1, а вместо 0.47 - 0.5.
В косоугольных проекциях плоскость проекции перпендикулярна главной координатной оси, а проекторы расположены под углом к ней. Таким образом, аксонометрические косоугольные проекции сочетают в себе свойства ортогональных и аксонометрических прямоугольных проекций. Наиболее употребимы два вида косоугольной проекции - фронтальная (косоугольная) диметрия (проекция Kabinett - кабине) и горизонтальная (косоугольная) изометрия (проекция Kavalier - кавалье) или военная перспектива. В случае фронтальной (косоугольной) диметрии при использовании правосторонней системы координат экрана плоскость проецирования перпендикулярна оси Z. Ось X направлена горизонтально вправо. Ось Z изображается по углом в 45º относительно горизонтального направления. Допускается угол наклона в 30º и 60º. При этом отрезки, перпендикулярные плоскости проекции, при проецирования сокращаются до 1/2 их истинной длины. На рис. приведена (аксонометрическая косоугольная) фронтальная диметрическая проекция куба со стороной A, там же показаны регламентируемые коэффициент сжатия, равный 0.5 и расположение осей.
В случае же (аксонометрической косоугольной) горизонтальной изометрии, как следует из названия, плоскость проецирования перпендикулярна оси Y а укорачивания по всем осям одинаковы и равны 1. Угол поворота изображения оси X относительно горизонтального направления составляет 30º. Допускается 45º и 60º при сохранении угла 90º между изображениями осей X и Z. Иллюстрация этого приведена на рис. .
Выведем выражения для матриц преобразования, используя теперь левостороннюю систему координат более естественную для машинной графики. Контрольные вопросы 1. Для чего используются проекции? 2. Какие виды проекций вы знаете? 3. Как определяется параллельная проекция? 4. Определите ортографическую проекцию. 5. Определите аксонометрическую проекцию. 6. Дайте определение видовых проекций. 7. Определите косоугольную проекцию. 8. Назовите наиболее распространенные виды косоугольной проекции.. 9. Напишите формулу косоугольного проецирования. 10. Начертите косоугольную проекцию длинного параллелепипеда, рассматриваемого со стороны длинной грани чуть сверху и сбоку. Центральная проекция
Наиболее реалистично трехмерные объекты выглядят в центральной проекции из-за перспективных искажений сцены. Центральные проекции параллельных прямых, не параллельных плоскости проекции будут сходиться в точке схода. В зависимости от числа точек схода, т.е. от числа координатных осей, которые пересекает плоскость проекции, различаются одно, двух и трехточечные центральные проекции. Иллюстрация одно-, двух- и трехточечной центральных проекций куба приведена на рис. .
Наиболее широко используется двухточечная центральная проекция. Выведем матрицу, определяющую центральное проецирование для простого случая одноточечной проекции (рис. ), когда плоскость проекции перпендикулярна оси Z и расположена на расстоянии d от начала координат. (Здесь используется удобная для машинной графики левосторонняя система координат).
Начало отсчета находится в точке просмотра. Ясно, что изображения объектов, находящиеся между началом координат и плоскостью проекции увеличиваются, а изображения объектов, расположенных дальше от начала координат, чем плоскость проекции уменьшаются. Из рис. видно, что для координат (X1,Y1) точки P1, полученной проецированием точки P0(X,Y,Z) в плоскость Z = d (плоскость экрана) выполняются следующие соотношения:
Такое преобразование может быть представлено матрицей 4×4
Для перехода к декартовым координатам делим все на z/d и получаем:
Если же точка просмотра расположена в плоскости проекции, тогда центр проекции расположен в точке (0, 0, -d). Рассматривая подобные треугольники, аналогично вышеописанному, можем получить:
Матрица преобразования в этом случае имеет вид:
Матрица M0 может быть представлена в виде:
т.е. преобразование проецирования выполняется для этого случая путем переноса начала координат в центр проецирования, собственно проецирования и обратного сдвига начала координат. Стереоизображения Существенное повышение наглядности изображения достигается использованием псевдостереоизображений. В этом случае каждым глазом надо рассматривать отдельный перспективный вид. Оба таких вида отображаются на экран дисплея. Для их разделения могут использоваться: - цветовое разделение, когда, например, изображение для левого глаза строится красным цветом, а для правого - синим и для просмотра используются цветные очки; недостаток этого способа состоит в том, что по сути дела можно формировать только простые каркасные изображения, но зато реализация проста и полностью используется пространственное разрешение дисплея; - пространственное-временное разделение, когда, например, изображение для левого глаза строится в четных строках, а для правого - в нечетных и для просмотра используются электронные или электромеханические очки, перекрывающие или левый или правый глаз на время прорисовки нечетных, четных строк, соответственно; этот подход может быть реализован на дисплеях с чересстрочной разверткой, позволяет выводить достаточно динамические цветные полутоновые изображения, но с уменьшением вдвое разрешения по вертикали; - временное разделение, когда для левого глаза используется одна страница видеопамяти, а для правого - вторая и происходит их переключение с достаточно большой частотой кадровой развертки; для перекрытия глаз также должны использоваться электронные или электромеханические очки; пространственное разрешение по строкам здесь не теряется. Кроме этого, статические цветные псевдостереоизображения могут быть получены последовательным фотографированием изображений для левого и правого глаз с последующим просмотром через стереоскоп. Используя результаты, полученные в предыдущем пункте, легко сконструировать матрицы преобразований для получения стереопроекций для левого и правого глаз. Контрольные вопросы 1. Дайте определение центральной проекции. 2. Что называется точкой схода в центральной проекции? 3. Сколько может быть главных точек схода? 4. Опишите свойства центральной проекции. 5. Определите косоугольную проекцию. 6. Напишите формулу центрального проецирования. 7. Начертите центральную проекцию длинного параллелепипеда, рассматриваемого со стороны длинной грани чуть сверху и сбоку. 8. Какие способы применяются для создания стереоизображений? 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

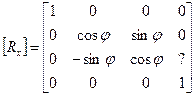












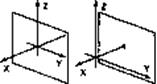 При ортографической проекции картинная плоскость совпадает с одной из координатных плоскостей или параллельна ей.
При ортографической проекции картинная плоскость совпадает с одной из координатных плоскостей или параллельна ей.











