А- стена без уступов, б- стена с уступами

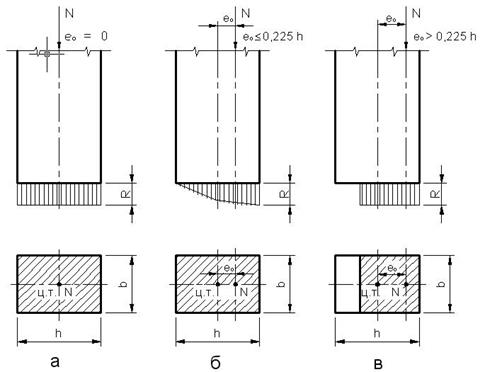
В стенах и столбах рассматриваемого этажа возникают продольные усилия N_i от веса стен и перекрытий вышележащих этажей, а от веса перекрытия рассматриваемого этажа – усилие Р_i . Сила N_i считается приложенной в центре тяжести сечения стены (столба) вышележащего этажа. Сила Р_i принимается приложенной с фактическим эксцентриситетом е относительно оси стены. Сила Р_i вызывает сжатие и момент М_р = Р_i х е , причем, если положение силы Р_i не фиксировано, то считают, что она приложена на расстоянии 1\3 длины заделки балки или настила от грани стены. Эпюри моментов по высоте стены каждого этажа имеет треугольную форму с максимальной ординатой в плоскости опирания перекрытия.

В зависимости от точек приложения расчетных сил N_i и Р_i различают элементы, работающие на центральное сжатие (рис.6 г ), когда равнодействующая N приложена в центре тяжести сечения, и элементы, работающие на внецентренное сжатие, когда сила N приложена на расстояние е_о от центра тяжести сечения (рис.6 б и в). Величина общего эксцентриситета относительно оси стены составляет

М_р

℮_о = -------

N_i + Р_i

Рис.6. Эпюры напряжений в кладке при прямоугольном сечении:

о- Центральное сжатие; б- внецентренное сжатие при ℮_о <0,225h;

в-внецентренное сжатие при ℮> 0,225h.

Расчет стен, простенков и столбов состоит в том, чтобы придать им необходимые размеры сечений и подобрать марки камня и раствора, соответствующие возникающим в сечениях напряжениям.

Центрально сжатые элементы

На центральное сжатие работают внутренние стены и столбы зданий, обычно нагруженные симметрично относительно центра тяжести сечения. Расчет центрально сжатых элементов каменных конструкций по первому предельному состоянию – по прочности и устойчивости (несущей способности) производится по следующим формулам:

при неармированной кладке

N ≤ φ х R х A;

при кладке, армированной продольными сетками

N ≤ φ х R_s.k х А;

при кладке, армированной продольными сетками

N ≤ φ х (0,85R х А + R_s х А_s);

где N- расчетная продольная сила от полной нагрузки, определяемая по формуле

N_ℓ

N= ---------

m_g

N_ℓ – расчетная продольная сила от длительно действующей части нагрузки;

N_кр – расчетная продольная сила от кратковременно действующей части нагрузки;

m_g – коэффициент,учитывающий влияние длительного действия нагрузки ( влияние ползучести) на несущую способность элементов толщиной менее 30см или с радиусом инерции сечения менее 8,7 см и принимаемый по табл.15.

Таблица 15

Коэффициенты m_дл

φ - коэффициент продольного изгиба, принимаемый по табл. ;

R - расчетное сопротивление сжатию неармированной кладки (см.табл.2…5);

А - площадь поперечного сечения элемента в см²

R_s.k. - расчетное сопротивление сжатию кладки армированной горизонтальными сетками, определяемое по формуле ;

R_s - расчетное сопротивление продольной арматуры (см.табл.16 );

А_s - площадь сечения продольной арматуры.

Таблица 16

Расчетные сопротивления арматуры R_s в кгс/см² в армированной кладке

Из формул видно, что расчетная нагрузка N, приходящаяся на элемент, должна быть меньше или равна несущей способности элемента. Как правило, центрально сжатые элементы каменных конструкций должны иметь такие размеры поперечных сечений, которые могли бы воспринять расчетную продольную силу N без помощи арматуры.

Если же размеры поперечных сечений элементов, принятые из конструктивных или архитектурных соображений. ограничены – имеют размеры меньшие, чем это требует расчет,- кладка таких элементов должна быть усилена арматурой. При центральном сжатии кладку следует армировать поперечными сетками, что более эффективно по сравнению с продольным армированием, так как уменьшает расход стали более чем наполовину.

Примеры расчета центрально сжатых элементов

Расчет кирпичных столбов

Исходные данные Требуется найти несущую способность

для примера 1. кирпичного столба первого этажа прис-

пособленного под магазин, в четырех-

этажном жилом доме.

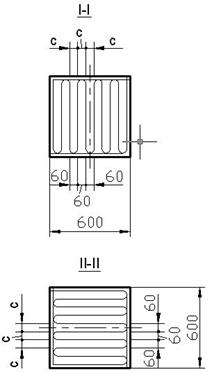
Столб сложен из глиняного кирпича пластического прессования марки 150 на растворе марки 50. Сечение столба 64 х 64см. Высота столба H=5,1м.

Нагрузка приложена центрально и состоит из постоянной G=486 кН и временной Р=168 кН.

Решение

Так как толщина элемента больше 30см, то влияние длительного действия нагрузки не учитывается – m_g= 1.

Полная расчетная нагрузка на столб

N= G + Р = 486 + 168 = 654 кН

Гибкость столба

λ_h = ℓ_о/h = 510/ 64 = 8

Упругая характеристика кладки из кирпича марки 150 на растворе марки 50 по табл.11 составляет

= 1000

Коэффициент продольного изгиба кладки столба по табл.12

φ= 0,92

Расчетное сопротивление кладки по табл. равно

R = 1,8 МПа = 1800 кПа

Площадь сечения столба

А= 64 х 64 = 4096см² > 3000см²

Коэффициент условий работы = 1,0

Несущая способность столба составляет

N_ст= φ х R х А= 0,92 х 1800 х 0,4096 = 678,3 кН >654кН

Несущая способность столба обеспечена.

На практике размеры сечения элементов и нагрузки обычно известны. Искомой величиной является напряжение в кладке σ и необходимые марки камня и раствора. Поэтому расчет столба в рассмотренном примере может быть выполнен в другом порядке.

Нам известна нагрузка N= 654 кН, площадь сечения столба

А = 4096см² = 0,4096м² и коэффициент продольного изгиба φ =0,92.

Определяем напряжение в кладке кирпичного столба

N 654

σ = -------- = ----------------- = 1736 кПа = 1,74 МПа

φ х А 0,92 х 0,4096

По табл. 2 принимаем кирпич марки 150 и раствор марки 50 или кирпич марки 100 на растворе марки 100. Им соответствует кладка с расчетным сопротивлением R= 1,8 МПа > σ= 1,74 МПа.

Исходные данные Подобрать марку керамических камней

для примера 2. и раствора для столба каркаса складского здания.

Сечение столба из конструктивных требований назначено 51х38см. Высота столба составляет 4,8м. Стойка нагружена центрально расчетной силой N= 238 кН.

Решение

Так как площадь сечения столба А= 51 х 38 = 1938см² < 3000см²,

то расчетное сопротивление кладки необходимо умножить на коэффициент условий работы = 0,8

Гибкость столба

λ_h = ℓ_о/h = 480/ 38 = 12,65

Упругая характеристика кладки по табл.

= 1000

Коэффициент продольного изгиба по табл.

φ= 0,82

Напряжение в кладке столба с учетом коэффициента условий работы

= 0,8

N 238

σ = -------- = --------------------------- = 1872 кПа = 1,872МПа

х φ х А 0,8 х 0,82 х 0,1938

По табл.2 принимаем керамические камни марки 125 на растворе марки 75 с расчетным сопротивлением R= 1,9 МПа.

Несущая способность столба в этом случае составит

N_ст= φ х х R х А= 0,82 х 0,8 х 1900 х 0,1938 = 241,55 кН >N=238кН

Первое предельное состояние ( прочность) столба обеспечена.

Расчет армированной кладки

При армировании кладки горизонтальными сетками расчет следует вести в такой последовательности.

По заданным размерам элемента определяют его гибкость λ и коэффициент продольного изгиба φ для неармированной кладки. Затем по величинам N, А и φ определяют напряжения в кладке

σ = N/ φ х А

По табл.2 находят расчетное сопротивление неармированной кладки R. Если величина R меньше величины σ, то необходимо кладку усилить арматурой.

Процент армирования кладки μ при горизонтальных сетках определяют по формуле

σ - R

μ = --------- х 100

2R_s

Шаг С между стержнями прямоугольной сетки определяют по формуле

200 х а_s

С = --------------- ;

μ х S

где а_s – площадь сечения одного стержня сетки в см²;

S – расстояние между сетками по высоте элементов в см.

Исходные данные Определить несущую способность столба

примера 3. трехэтажного промышленного здания с сеткой

колонн 6х12м.

Для кладки столба применить сплошные бетонные камни марки 150 и раствор марки 75. Расчетная нагрузка на столб N= 1250кН приложена центрально. Сечение столба 60х60см. Высота столба Н=4,5м.

Решение

Так как толщина элемента больше 30см, то влияние длительного действия нагрузки не учитывается – m_g = 1

Гибкость столба

λ_h = ℓ / h = 450/ 60 = 7,5

Упругая характеристика кладки из сплошных бетонных блоков на растворе марки 75 по табл. 11 составляет

= 1500

Коэффициент продольного изгиба столба по табл.12 равен

φ= 0,955

Расчетное сопротивление кладки по табл. составляет

R= 2,8 МПа = 2800 кПа

Площадь сечения столба

А= 60 х 60 = 360 см²= 0,36м²

Коэффициент условий работы = 1,0

Напряжение σ, возникающее в кладке столба под влиянием расчетной нагрузки N

N 1250

σ = ---------- = --------------------------- = 3636 кПа >R= 2800кПа

φ х х А 0,955 х 1,0 х 0,36

Расчетное сопротивление кладки столба меньше, чем возникающие в кладке напряжения. Поэтому столб необходимо армировать. Так как гибкость столба λ_h = 7,5 <15, то армирование производится горизонтальными сетками.

Определим процент армирования μ, при котором R= 2800 кПа увеличится до R_s.k. = 3700 кПа. Сетки проектируем из обыкновенной проволоки В-I с расчетным сопротивлением R_s = 180 МПа = 180000 кПа. Требуемый процент армирования

( σ- R)¹⁰⁰ (3700-2800)х 100

μ = ------------- = ------------------------ = 0,252%

2R 2х 180000

Вносим поправку в величину упругой характеристики кладки, так как упругая характеристика была принята для неармированной кладки

R 2800

α_S = α х --------- = 1500 -------- = 1150

R_s.k 3700

Коэффициент продольного изгиба при α_s =1150 равен φ = 0,93

Напряжение в кладке столба, армированного горизонтальными сетками при φ = 0,93

σ =--------------------- = 3734 кПа >R_s.k =3700кПа

0,93 х 0,36 х 1,0

Уточним процент армирования

3734-2800

μ = ----------------- х 100 = 0,26%

2 х 180000

Назначаем сетку из стержней диаметром 5мм с а_s = 0,196 см², а расстояние между сетками s = 30см.

Определяем шаг стержней в горизонтальных сетках

200 х а_s 200 х 0,196

с= ------------ = ------------------- = 5,02 см

μ х s 0,26 х 30

Армирование столба прямоугольными горизонтальными сетками показана на рис.7

Несущая способность столба, армированного сетками. составит

N_ст = φ х R_s.k х х А = 0,93 х 3750 х 1,0 х 0.36 = 1255,5 кН ≈ N=1250кН

Несущая способность столба, армированного горизонтальными сетками, обеспечена.

Армирование кладки продольными стержнями производится в случае большой гибкости элементов ( при λ_h >15). Так же, как и при армировании поперечными сетками, величины R, А и φ обычно заранее известны и расчет состоит в определении величины процента продольного армирования μ

σ – 0,85 R

μ = ----------------- х 100,

R_s

где σ – напряжение в кладке без учета работы арматуры;

R- расчетное сопротивление кладки сжатию;

R_s – расчетное сопротивление арматуры

Исходные данные Рассчитать столб сечением 64 х 51см сложен-

примера 4. ный из кирпича марки 100 на растворе марки 75 Высота столба Н= 8,4м.

Расчетная нагрузка на столб N= 570 кН приложена центрально.

Решение

Так как минимальная толщина столба больше 30см, то влияние длительного действия нагрузки не учитывается – m_g=1,0

Гибкость столба

ℓ 840

λ_h = ----- =------- = 16,5 > 15

h 51

Упругая характеристика кладки столба по табл. составляет

= 1000

Коэффициент продольного изгиба столба по табл. равно

φ= 0, 73

Расчетное сопротивление кладки по табл. составляет

R= 1,7 МПа = 1700 кПа

Площадь сечения столба

А= 64 х 51 = 3264 см²= 0,3234 м²

Определяем напряжения в кладке без учета работы арматуры

N 570

σ = ---------- = --------------------------- = 2400 кПа >R= 1700кПа

φ х А 0,73 х 0,3234

В связи с тем, что напряжения в кладке σ больше расчетного сопротивления R и гибкость элемента λ_h> 15, усиление столба производим продольным армированием.

Необходимый процент армирования при стали класса А-II с расчетным сопротивлением R_s – 240 МПа = 240000 кПа

σ – 0,85 R 2400 –0,85 х 1700

μ = ----------------- х 100 = ---------------------- х 100=0,4%

R_s 240000

Площадь поперечного сечения арматуры

А х μ 3264 х 0,4

А_s = --------- = ------------------ = 13,06 см³

100 100

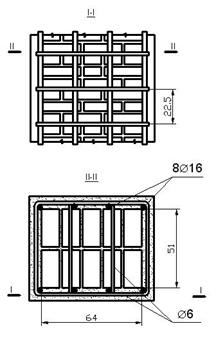
Принимаем наружное армирование столба 8 Ø16АII с

А_s=16,08см²>13,06см². Хомуты устанавливаем через три ряда кладки S=22,5см<15d_s = 15 х 1,6 = 24 см. Диаметр хомутов назначаем 6мм. Армирование столба приведено на рис.8

Рис.8 К примеру 5

Внецентренно сжатые элементы

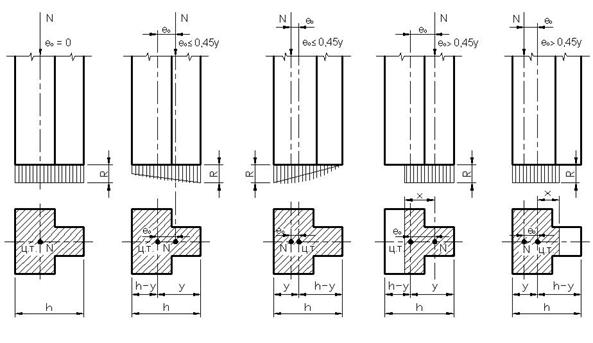
На внецентренное сжатие обычно работают наружные стены,

простенки и другие элементы, нагруженные с эксцентриситетом ℮_о относительно центра тяжести сечения. Несущая способность элементов каменных конструкций при внецентренном сжатии зависит не только от прочности кладки, но также и от величины относительного эксцентриситета ℮_о/h или ℮_о/у. Вот почему при рассмотрении внецентренного сжатия различают два случая:

-случай малых эксцентриситетов, когда ℮_о ≤ 0,45h/2 (℮_о ≤ 0,45у) и все сечение сжато;

-случай больших эксцентриситетов, когда ℮_о ≥ 0,45h/2 (℮_о ≤ 0,45у) и у грани, менее напряженной, возникают растягивающие усилия.

Случай малых эксцентриситетов. Расчет внецентренно сжатых элементов каменных конструкций при малых эксцетриситетах, не выходящих из ядра сечения (℮_о < 0,45у), производится по формулам:

- при неармированной кладке

N ≤ φ х R х А х Ψ,

- при армировании кладки горизонтальными сетками

N≤ φ х R_sk А х Ψ,

где N, φ, R,А – имеют те же значения, что и в формулах центрального сжатия;

Ψ – коэффициент, учитывающий влияние эксцентриситета, определяется по формулам табл. ;

R_sk –прочность кладки. армированной горизонтальными сетками.

Расчет элементов из неармированной кладки при внецетренном сжатии с малым эксцентриситетом производится в таком порядке;

-по моменту М и силе N, действующим в сечении, определяют эксцентриситет ℮_о ;

-по заданным размерам элемента и упругой характеристике кладки опредяляют гибкость элемента λ_h (λ_ч) и коэффициент продольного изгиба φ

-по заданным величинам N, А и найденному φ определяют напряжения в кладке:

при прямоугольном сечении

2 ℮_о

N (1+ -------

h

σ = ------------------------ ;

φ х А

при тавровом сечении

℮ _о

N (1+ -------

h-у

σ = ------------------------ ;

φ х А

-табл.2…5 находят расчетное сопротивление кладки R, равное или

ближайшее больше величины σ, и соответствующие им марки камня и раствора

Таблица

Формулы для определения коэффициента φ , учитывающего влияние эксцентриситета при внецентренном сжатии

Если из имеющихся марок камня и раствора не может быть получена

кладка с расчетным сопротивлением R≥ σ, ее армируют поперечными сетками или продольными стержнями. На практике как и при центральном сжатии, удобнее по заданным величинам N, A, φ,℮_оопределять напряжения в кладке σ и необходимый процент армирования μ по формулам:

при тавровом сечении

℮_о

N (1+ ------- )

h-у

σ = ------------------------ ≤ R_sk

φ х А

и

(σ – R) х 50

μ = ---------------------- ;

2℮_о

R_s (1- --- )

у

при прямоугольном сечении

2℮_о

N (1+ ------- )

h

σ = ------------------------ ≤ R_sk

φ х А

и

(σ – R) х 50

μ = ---------------------- ;

4℮_о

R_s (1- --- )

h

где R_s- расчетное сопротивление арматуры.

Случай больших эксцентриситетов (℮_о >0,45у) .При больших

эксцентриситетах краевое напряжение кладки сжатию больше, чем при центральном сжатии, и близко к расчетному сопротивлению кладки смятию.

Расчет внецентренно сжатых элементов с большими эксцентриситетами производится по формуле

N= φ₁ х R х А х Ψ

Коэффициент Ψ определяется по формулам, приведенным в табл…

Подставив значение Ψ в формулу для неармированной кладки получим выражения для расчета внецентренно сжатых элементов с большими эксцентриситетами:

при тавровом сечении

N= φ₁ х R х А х √ А/А_с ;

при прямоугольном сечении

2℮ _о

N= φ₁ х R х А х √ (1- ------- )² ;

h

где А- площадь всего сечения элемента;

А_с- часть площади сечения, уравновешивающая внецентренно приложенную силу ( при прямоугольной эпюре напряжений);

φ₁ –приведенный коэффициент продольного изгиба при ℮_о >0,45у

Приведенный коэффициент продольного изгиба равен

φ + φ_с

φ₁ ----------- ;

где φ – коэффициент продольного изгиба для всего сечения А;

φ_с – коэффициент продольного изгиба для сжатой части сечения А_с при гибкости:

для таврового сечения:

H

λ_hс = -------------- ;

2(у -2е_о )

для прямоугольного сечения

H

λ_hс = -------------- ;

h -2е_о

(Н- высота элемента при однозначной эпюре момента по всей длине)

Площадь А_с и высоту h_с сжатой части сечения определяют по формулам:

для таврового сечения

А_с = 2 (у - ℮_о )в;h_с = 2 (h - ℮_о );

для прямоугольного сечения

2℮ _о 2℮ _о

А_с = А х (1- ---- ) ; h_с = h х (1- ---- );

h h

где в – ширина сжатой полки в зависимости от направления эксцентриситета (рис.9);

h – высота сечения;

у- расстояние от центра тяжести сечения до края сечения в сторону эксцентриситета.

Рис.9 Эпюры напряжений в кладке при тавровом сечении:

а- центральное сжатие; б- внецентренное сжатие при ℮_о < 0,45у с эксцентриситетом в сторону ребра; ℮- то же, в сторону полки; г- внецентренное сжатие при ℮_о > 0,45у с эксцентриситетом в сторону ребра; д- то же в сторону полки.

Используя выражения несущей способности по заданным расчетным усилиям N и М и размерам поперечного сечения определяются фактические напряжения в кладке σ по формулам:

при тавровом сечении

N

σ = --------------------- ;

φ₁ х А_с х √ А_с/А

при прямоугольном сечении

N

σ = ---------------------------------- ;

2℮ _о

φ₁ х А_с х √ (1- ---- )²;

h

Затем по табл… принимают соответствующую марку камня и раствора и вычисляют несущую способность элемента по расчетному сопротивлению кладки.

Элементы, работающие на внецентренное сжатие, дополнительно рассчитывают на центральное сжатие в плоскости, перпендикулярной к плоскости момента.

Примеры расчета внецентренно сжатых элементов.

Исходные данные Рассчитать простенок третьего этажа

примера 5. пятиэтажного здания в связи с надстройкой

шестого этажа. Размеры простенка в плане и нагрузки на простенок приведены на рис.10. Высота простенка составляет Н= 3,2 м.

Простенок нагружен расчетной постоянной нагрузкой G= 500 кН и нагрузкой от междуэтажного перекрытия Р= 143 кН, приложенной с эксцентриситетом 15см.

Решение.

Толщина стены превышает 30см и поэтому влияние длительного действия нагрузки можно не учитывать - m_g =1.

Полная нагрузка на простенок

N= G+ Р= 500 + 148 = 643 кН.

Нагрузка от перекрытия создает момент относительно оси простенки

М= Р х ℮ = 143х 15 = 2140 кН.см.

Эксцентриситет приложения полной нагрузки N относительно оси простенка

M 2140 h 39

℮ _о = ---- = ------ = 3,33см<0,45 --- = 0,45 --=

N 643 2 2

= 8,8 см.

Имеет место внецентренное сжатие с

малым эксцентриситетом.

Гибкость простенка

H 320

λ_hс = ------- = ----- = 8,42

h –2℮_о38

Упругая характеристика кладки из керамических камней на растворе марки 25 и выше по табл.11

= 1000.

Рис. 10 . К примеру 5.

Коэффициент продольного изгиба по табл.

φ =0,9

Площадь простенка, вводимая в расчет

А= 130 х 38 = 4940 см² = 0,494 м²

Напряжения в кладке простенка

2е_о 2х 3,33

N (1+ ---- ) 643 ( + --------- )

h 38

σ = --------------------- = ------------------ = 1700кПа=1,7МПа

φ х А 0,9 х 0,494

По табл.2 принимаем керамические камни марки 100 на растворе марки 75 с расчетным сопротивлением R= 1,7 МПа или камни марки 150 на растворе марки 50 с расчетным сопротивлением R= 1,8 МПа.

Несущая способность простенка

φ х R х А 0,9 х 1,7 х 10³х 0.494

N₍₁₀₀₎= ------------ = ------------------------------ = 643,4 кН≈ N= 643кН.

2е_о 2 х 3,33

1 + ------- 1+ -----------

h 38

0,9 х 1,8 х 10³х 0,494

N₍₁₅₀₎= -------------------------- = 680,9 кН > N= 643кН.

2 х 3,33

1+ -----------

Прочность простенка в обеих случаях обеспечена.

Исходные данные Рассчитать простенок первого этажа

примера 6. пятиэтажного здания в связи с

надстройкой шестого этажа. Размеры простенка и нагрузки на простенок приведены на рис.11. Высота простенка

составляет Н= 3,6м.

Простенок нагружен расчетной продольной силой G= 730 кН и нагрузкой от перекрытия 1-го этажа Р= 170 кГ, приложенной с эксцентриситетом е = 15см.

Решение.

Полная нагрузка на простенок 1-го этажа n= 730 + 170 = 900 кН.

Нагрузка от перекрытия 1-го этажа создает момент относительно оси простенка.

М= 170 х 15 = 2550 кН.см

Эксцентриситет приложения полной нагрузки N относительно оси простенка

M 2550 h 38

е_о = ---- = ------ = 2,85см<0,45 --- = 0,45 --=

N 900 2 2

= 8,8 см.

Имеет место случай малых

эксцентриситетов.

Гибкость простенка

H 360

λ_hс = ------- = ----- = 9,5

h 38

Упругая характеристика кладки из керамических камней на растворе марки 25 и выше по табл.

a = 1000.

Рис.11 . К примеру 6

Коэффициент продольного изгиба по табл.

φ =0,885

Площадь простенка, вводимая в расчет

А= 130 х 38 = 4940 см² = 0,494 м²

Напряжения в кладке простенка

2е_о 2х 2,85

N (1+ ---- ) 900 ( + --------- )

h 38

σ = --------------------- = ------------------ = 2370кПа=2,37МПа

φ х А 0,885 х 0,494

Простенок сложен из керамических камней марки 150 на растворе марки 50 с расчетным сопротивлением R= 1,8 МПа.

Так как σ = 2,37 МПа >R= 1,8 МПа, то кладку простенка необходимо армировать. При гибкости простенка λ_hс = 8,42 <15 принимаем сетчатое армирование простенка из обыкновенной проволоки ВI с R_s = 180 МПа.

Определяем процент армирования μ, при котором расчетное сопротивление армированной кладки R_s.c. = 2,4 МПа ≈ σ

(σ – R) х 50 (2,4 – 1,8) х 50

μ = ---------------------- = --------------------- = 0,24%

4 е_о 4 х 2,85

R_s (1- --- ) 180 (1----------)

h 38

Так как кладка армирована, необходимо внести поправку в величину упругой характеристики кладки и повторить расчет.

Упругая характеристика армированной кладки

R 1,8

= --------- = 1000 ------ = 750

R_s.k. 2,4

Коэффициент продольного изгиба при гибкости λ_hс = 8,42 и = 750

по табл. равен φ = 0,86

Напряжения в кладке простенка при φ = 0,86

2х 2,85

900 ( + --------- )

σ = --------------------- = 2436кПа=2,436МПа

0,86 х 0,494

Процент армирования кладки при σ= 2,436 МПа

(2,436-1,8) х 50

μ = ---------------------- = 0,253%

4 х 2,85

180 (1----------)

Расчетное сопротивление армированной кладки при внецентренном сжатии из кирпича марки 150 на растворе марки 50 при μ = 0,253%

2 R_s 4 е_о 2 х 180 4 х 2,85

R_s.k. = R + -------- μ х 1- ----- = 1,8 + ------ х 0,253 (1- --------) = 2,44МПа

100 h 100 38

Несущая способность простенка из кладки. армированной сетками

1 1

N= φ х R_s.k. х А ------- = 0,86 х 2,44 х (1000) х 0,494 х ------- = 901,4кН>900 кН

2 е_о 2х2,85

1+ ---- 1+------

h 38

Шаг между стержнями сетки при диаметре стержней 5мм с а_s = 0,196см² и при шаге сеток в кладке s= 22,5 см.

200 х а_s 200 х 0,196

с = ---------- = ---------------- = -6,88 см

μ х s 0,253 х 22,5

Назначаем шаг стержней в сетке равным 6,0 см. Армирование простенка показано на рис.11

Исходные данные Подобрать марки камня и раствора для

примера 7 кирпичного простенка с пилястром

(таврового сечения) на 3-ем этаже

промышленного здания.

Высота простенка составляет 5.1 м. Нагрузки на простенок и его размеры в плане приведены на рис.12 . Простенок загружен продольной силой от вышележащих этажей N₁ = 1150 кН и нагрузкой от междуэтажного перекрытия Р= 150 кН, приложенной к пилястру.

Решение

Так как толщина простенка больше 30см, то влияние длительного действия нагрузки не учитывается = m_g=1.

Определяем геометрические

характеристики простенка:

- площадь сечения.

А = А_ст + А_пил. = 155 х 64 + 64 х 52 =

=9920 + 3320 = 13240 см²

-статический момент сечения относительно грани пилястра

h_ст h_ст

S= А_ст ( ----- + h _пил.) + А_пил.----- =

2 2

64 52

= 9920 ( ---- + 52) + 3320---- = 918000см³

2 2

-положение центра тяжести сечения

относительно грани пилястра

Рис. 12. К примеру 7.

S 918000

у_о=----- = -------- = 69 см;

А 13240

-расстояние от центра тяжести сечения до грани стены

у= d – у_о = 116 – 69 = 47 см.

Эксцентриситет приложения нагрузки относительно центра тяжести

сечения

-N₁ х е₁ + Р х е₁ - 1150+ 15 + 150 х 43

е_о = ------------------- = ---------------------------- = - 8 см,

N₁ + Р 1150 + 150

h_ст 64

где е₁ = h_пил + ------- - у_о = 52 + ---- - 69 = 15см;

2 2

h_пил 52

е₂ = у_о + ------- = 69 - ---- = 43см;

2 2

Эксцентриситет приложения нагрузки е_о = 8см < 0,45у = 0,45х47=21см. Следовательно, имеет место случай малых эксцентриситетов.

Момент инерции сечения простенка относительно центра тяжести

155х 64³ 64 64х 52³ 52

I = ---------- + 155 х 64 ( 47- -----)² + -------- + 64 х 52 (69- ---)² =12521408см⁴

12 2 12 2

Радиус инерции сечения простенка

I 12521408

ч= √ --- = √ ------------- = 31 см.

А 13240

Упругая характеристика кладки на растворе марки 25 и выше по табл.

= 1000

Приведенная гибкость простенка высотой ℓ_о = Н= 5,1м

ℓ_о 510

λ_ч = ------- = ----- = 16,5

ч 31

Коэффициент продольного изгиба простенка по табл.

φ =0,985

Напряжения в кладке простенка

℮_о 8

N (1+ ---- ) ( 1150+150) (1+ -------- )

h-у 116-47

σ = --------------------- = ------------------------------- = 1160кПа=1,16МПа

φ х А 0,885 х 0,494

По табл. 2 принимаем кирпич марки 100 на растворе марки 25. Им соответствует кладка с расчетным сопротивлением R= 1,3 МПа > σ = 1,16 МПа.

Несущая способность простенка при принятой кладке

1 1

N=φ х R_. х А ------- = 0,985 х 1,3 х(1000) х 1,324 х ------------ = 1519кН>1300 кН

е_о 8

(1+ ---- ) ( 1+--------- )

h-у 116-47

Несущая способность простенка обеспечена.

Исходные данные Рассчитать простенок первого этажа

примера 8. промышленного здания с размерами,

приведенными в примере 7.

Нагрузки на простенок приведены на рис.13 . Величины нагрузок N₁=2200кН; Р= 250кН и полная N = 2150кН.

Высота простенка Н= 6,1м.

Решение

Так как размеры сечения не изменились, то и геометрические характеристики сечения остались неизменными:

-площадь сечения А= 13240см^2;

-момент инерции I= 12521408см⁴;

-радиус инерции ч= 31см;

-положение центра тяжести сечения

у_о= 69см;

-расстояние границ стены у-47см.

эксцентриситет равнодействующей

всех сил N= 2450 кН относительно центра тяжести сечения

Рис.13. К примеру 8

-N₁ х е₁ + Р х е₂ - 2200х 15 + 250 х 43

е_о = ------------------- = ---------------------------- = 9,1 см.<

N 2450

< 0,45у = 0,45х47 = 21см.

Имеет место случай малых эксцентриситетов.

Упругая характеристика кладки = 1000

Приведенная гибкость простенка λ_ч = 16,5

Коэффициент продольного изгиба φ = 0,985

Напряжения в кладке простенка

℮_о 9,1

N (1+ ---- ) 2450 (1+ -------- )

h-у 116-47

σ = --------------------- = ------------------------------- = 2130кПа=2,13МПа

φ х А 0,985

По табл.2 принимаем кирпич марки 100 на растворе марки 50. Этой кладке соответствует расчетное сопротивление R= 1,5МПа. Так как R< σ , то столб армируем горизонтальными прямоугольными сетками.

Необходимый процент армирования простенка при прямоугольных сетках из обыкновенной проволоки В-I с R_s = 180 МПа.

(σ – R) х 50 (2,4 – 1,8) х 50

μ = ---------------------- = --------------------- = 0,286%

2 е_о 2х 9,1

R_s (1- --- ) 180 (1----------)

у 47

Так как кладка армирована, то вносим поправку в величину упругой характеристики кладки и повторяем расчет.

Упругая характеристика армированной кладки при R_s.k = 2,15Ма

R 1,5

= --------- = 1000 ------ = 700

R_s.k. 2,15

Коэффициент продольного изгиба армированной кладки при λ_ч = 16,5 и = 700 по табл.

φ = 0,977

Расчетное сопротивление армированной кладки при μ= 0,3%

2R_s ℮_о 2х180 2х9,1

R_s.k= R + ---------- μ (1- -----) = 1,5+ --------- х 0,3 (1- ------)=2,16МПа

100 у 100 47

Несущая способность простенка из армированной кладки при внецентренном сжатии

1 1

N=φ х R_s.k._. х А ----- = 0,977 х 2,16х(1000) х 1,324 х -------- =2468,5кН>2450 кН

℮_о9,1

(1+ ---- ) (1+------- )

h-у 116-47

Прочность армированного простенка достаточна для восприятия действующей нагрузки.

Исходные данные Подобрать необходимые марки камня и

примера 9. раствора для простенка прямоугольного

сечения и проверить его несущую спо-

собность.

Высота простенка составляет Н= 4,2м. Размеры сечения простенка в х h = 103 х 51см. Простенок нагружен продольной силой N= 230кН и силой Р=190кН, приложенной с эксцентриситетом ℮ = 18,5см. Нагрузки на простенок приведены на рис.14.

Решение.

Площадь простенка составляет А = 103х51 = 5253см² > 3000см²

Следовательно, влияние длительного действия нагрузки можно не учитывать – m_g =1.

Изгибающий момент от действия силы Р

М= Р х ℮= 190 х 18,5 = 3515кНсм

Эксцентриситет приложения полной

нагрузки

М 3515

℮_о = ------ = ------ = 15,3 см

N 230

Имеет место случай больших

эксцентриситетов, так как

h 51

℮_о = 15,3см > 0,45 – = 0,45 х --- = 11,5см.

2 2

Принимаем упругую характеристику кладки, отвечающу марке

раствора 25 и выше (см. табл. )

a = 1000

Гибкость сжатой части простенка и коэффициент продольного изгиба

для нее

λ_п = ----- = 8, 25; φ = 0,91

Гибкость сжатой части простенка и коэффициент продольного изгиба

для нее

Не нашли, что искали? Воспользуйтесь поиском по сайту: