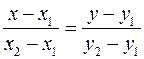|
|
Прямоугольные координаты на плоскости.
x = x'cosφ - y'sinφ + α, y = x'sinφ + y'cosφ + β
В частности, если
x = х' + α, у = у' + β - формулу преобразования координат при параллельном переносе системы координат Если же точки 0 и 0' совпадают, то x = x'cosφ - y'sinφ, y = x'sinφ + y'cosφ.
- формулы преобразования координат при повороте системы координат вокруг начала на угол φ
ПРЯМАЯ НА ПЛОСКОСТИ.
Прямая на плоскости
следует, что
- угловой коэффициент относительно выбранной системы координат. В частности, для прямоугольной системы координат (0, k = tgα, где α – угол между осью ОХ и любым направляющим вектором прямой l. Угол α называется углом наклона прямой l к оси ОХ.
Если прямая l параллельна оси ОY, то l пересекает ось OХ в некоторой точке Р(а,0). Тогда все точки прямой и только они удовлетворяют соотношению x = a - уравнение прямой, проходящей через точку параллельно оси ОУ. Заметим, что в качестве направляющего вектора такой прямой можно взять вектор Пусть прямая l проходит через точку A (а,b) и имеет угловой коэффициент k. Возьмем произвольную точку М (х,у) на прямой l. Тогда Следовательно,
Отсюда y – b = k (x-а) -уравнение прямой с угловым коэффициентом k. Общее уравнение прямой. Уравнение прямой в отрезках.
Пусть задана некоторая афинная система координат OXY. Теорема. Любая прямая l системе координат ОX задается линейным уравнением вида
Аx + By + С = О, (1)
где А, В, С Уравнение вида (1) - общее уравнение прямой. Пусть в уравнении (1) все коэффициенты А, В и С отличны от нуля. Тогда
-Ах-By=-С, и Обозначим -С/А=а, -С/B=b. Получим
- уравнение в отрезках. Действительно, числа |а| и |b| указывают на величины отрезков, отсекаемых прямой l на осях ОХ и OY соответственно. Пусть прямая l задана общим уравнением (1) в прямоугольной системе координат и пусть точки M1(x1,у1) и М2(х2,у2) принадлежит l. Тогда Аx1 + Ву1 + С = Ах2 + Ву2 + С, то есть A(x1-x2) + В(у1-у2) = 0. Последнее равенство означает, что вектор
Рассмотрим вектор
Следовательно, вектор
Параметрическое и каноническое уравнения прямой. Уравнение прямой, проходящей через две заданные точки.
и так как
Если обозначить - радиус-векторы соответственно точек M и M0, то
- уравнение прямой в векторной форме. Так как x = x0 + mt, y = y0 + nt
- параметрическое уравнение прямой. Отсюда следует, что
- каноническое уравнение прямой.
Наконец, если на прямой l заданы две точки M1(х1,у1) и M2(x2,у2), то вектор
- уравнение прямой проходящей через две заданные точки.
Взаимное расположение двух прямых.
Пусть прямые l1 и l2 заданы своими общими уравнениями l1: А1х + В1у + С1 = 0, (1) l2: А2х + В2у + С2 = 0.
Теорема. Пусть прямые l1 и l2 заданы уравнениями (1). Тогда и только тогда: 1) прямые пересекаются, когда не существует такого числа λ, что A1=λA2, В1=λB2; 2) прямые совпадают, когда найдется такое число λ, что А1=λA2, B1=λB2, С1=λС2; 3) прямые различны и параллельны, когда найдется такое числе λ, что А1=λA2, В1=λВ2, С1
Пучок прямых
Пучком прямых называется совокупность всех прямых на плоскости, проходящих через некоторую точку, называемую центром пучка. Для задания уравнения пучка достаточно знать какие-либо две прямые l1 и l2 , проходящие через центр пучка. Пусть в аффинной системе координат прямые l1 и l2 заданы уравнениями l1: A1x + B1y + C1 = 0, l2: A2x + B2y + C2 = 0.
Уравнение: A1x + B1y + С + λ (A2х + В2y + C) = 0 - уравнение пучка прямых, определяемого уравнениями l1 и l2
В дальнейшем, под системой координат будем понимать прямоугольную систему координат.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 Пусть дана старая и новая прямоугольные системы координат, соответственно (0,
Пусть дана старая и новая прямоугольные системы координат, соответственно (0, 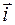 ,
, 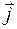 ) и (О',
) и (О', 

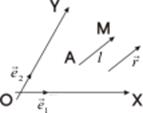 Пусть в плоскости α задана афинная система координат (0,
Пусть в плоскости α задана афинная система координат (0, 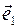 ,
,  ) и прямая l, принадлежащая этой плоскости α. Составим уравнение прямой l. Заметим, что положение прямой l однозначно определено, если известен вектор, коллинеарный этой прямой и называемый направляющим вектором прямой, и точка, через которую прямая проходит. Очевидно, что в качестве направляющего вектора прямой можно взять любой вектор, коллинеарный данной прямой. Пусть
) и прямая l, принадлежащая этой плоскости α. Составим уравнение прямой l. Заметим, что положение прямой l однозначно определено, если известен вектор, коллинеарный этой прямой и называемый направляющим вектором прямой, и точка, через которую прямая проходит. Очевидно, что в качестве направляющего вектора прямой можно взять любой вектор, коллинеарный данной прямой. Пусть 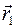 = (m1,n1) и
= (m1,n1) и 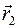 =(m2,n2) - какие-либо направляющие векторы прямой l. Тогда из необходимого и достаточного условия коллинеарности двух векторов
=(m2,n2) - какие-либо направляющие векторы прямой l. Тогда из необходимого и достаточного условия коллинеарности двух векторов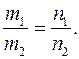 Если прямая l не параллельна оси OY, то
Если прямая l не параллельна оси OY, то  следовательно,
следовательно,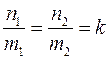
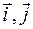 )
)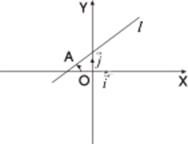
 (0,р), где р - произвольное отличное от нуля число. В этом случае, как видим угловой коэффициент прямой не существует.
(0,р), где р - произвольное отличное от нуля число. В этом случае, как видим угловой коэффициент прямой не существует.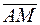 =(х-а, у-b) - направляющий вектор прямой l.
=(х-а, у-b) - направляющий вектор прямой l.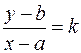
 R и А2 + В2
R и А2 + В2 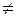 0. Обратно, любое уравнение вида (1) задает прямую.
0. Обратно, любое уравнение вида (1) задает прямую. .
.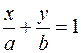
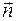 =(А,В) ортогонален вектору
=(А,В) ортогонален вектору 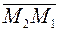 =(x1-x2,у1-у2). т.е.
=(x1-x2,у1-у2). т.е. 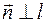 Вектор
Вектор 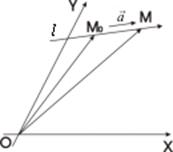 Пусть в афинной системе координат (0, X, Y) задана прямая l, ее направляющий вектор
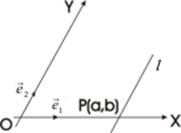
Пусть в афинной системе координат (0, X, Y) задана прямая l, ее направляющий вектор 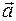 = (m,n) и точка M0 (x0,y0) принадлежащая l. Тогда для произвольной точки M (x,у) этой прямой имеем
= (m,n) и точка M0 (x0,y0) принадлежащая l. Тогда для произвольной точки M (x,у) этой прямой имеем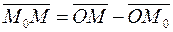
 то
то 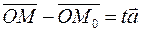 .
. и
и 
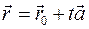
 =(х0,у0), то
=(х0,у0), то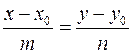
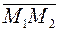 =(х2-х1,y2-у1) является направляющим вектором прямой l. Тогда
=(х2-х1,y2-у1) является направляющим вектором прямой l. Тогда