
|
|
Линейная зависимость векторов.
Пусть дана система векторов
и α1, α2,...αn - действительные числа. Тогда векторы вида
называются линeйнoй комбинaциeй вeктоpов cиcтeмы (1). Определение. Система векторов (1) называется линейно зависимой, если существует такая линейная комбинация этих векторов, равная нулевому вектору, т.е.
и хотя бы одно из чисел Определение. Система (1) называется линейно независимой, если равенство (2) возможно тогда и только тогда, когда все числа αi=0. Определение. Если какой-либо вектор
то говорят, что вектор Теорема. Для того чтобы векторы системы (1) были линейно зависимы (n>1), необходимо и достаточно, чтобы по крайней мере один из них линейно выражался через остальные. Следствие. Если векторы системы (1) линейно независимы, то ни один из них нельзя линейно выразить через остальные. В частности, ни один из них не может быть нулевым.
Теорема. Для того чтобы два вектора были линейно зависимы, необходимо и достаточно, чтобы они были коллинеарны. Следствие. Два вектора линейно независимы тогда и только тогда, когда они неколлинеарны.
Теорема. Любой вектор
причем это разложение единственно. Теорема. Для того чтобы три вектора были линейно зависимы, необходимо и достаточно, чтобы они были компланарны. Следствие. Три вектора линейно независимо тогда и только тогда, когда они некомпланарны.
Теорема. Любой вектор
причем это разложение единственно. Tеорема. Любые четыре вектора линейно зависимы.
Определение.Говорят, что два лежащих в плоскости α линейно независимых вектора Итак: 1) любая пара лежащих в данной плоскости неколлинеарнах векторов образует базис на этой плоскости; 2) любая тройка некомпланарных векторов образует базис в пространстве.
Координаты на прямой. Прямая l, на которой задана точка 0, называемая началомкоординат, задан единичный вектор Пусть М - произвольная точка прямой. Тогда вектор
линеарен вектору Так как Обратно, для каждого действительного числа х найдется единственная точка М оси l, координата которой равна х. Таким образом, положение любой точки координатной оси однозначно определяется заданием координаты этой точки.
Координаты на плоскости.
Пусть на плоскости α заданы две координатные оси ОХ и OY с неколлинеарными ортами Точка 0 называется началом кооpдинат, векторы
Числа х и у называются афинными координатами точки М в системе (0, (записывается: М(х,у)). Вектор Афинная система координат (0, Теорема. Пусть
Тогда Следствие 1. Пусть даны точки А (х1,y1) и В (х2,у2). Тогда
Следствие 2. Два вектора
Афинная система координат (0, 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 (1)
(1)
 (2)
(2) .
.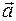 можно представить в виде линейной комбинации векторов системы (1), т.е.
можно представить в виде линейной комбинации векторов системы (1), т.е.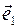 и
и  этой плоскости, т.е. представить в виде:
этой плоскости, т.е. представить в виде:
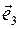 , т.е. представить в виде:
, т.е. представить в виде:
 (любые три линейно независимых вектора
(любые три линейно независимых вектора  ) образуют на этой плоскости (в пространстве) базис, если любой вектор, лежащий в этой плоскости α (любой вектор пространства), может быть представлен в виде линейной комбинации векторов
) образуют на этой плоскости (в пространстве) базис, если любой вектор, лежащий в этой плоскости α (любой вектор пространства), может быть представлен в виде линейной комбинации векторов  , называемый ортом, называется координатнойосью.
, называемый ортом, называется координатнойосью. кол-
кол- . Вектор
. Вектор 



 .
.
 .
.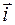 и
и 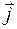 .
.