
|
|
Линейные операции над векторами.А.Д. Ходалевич Р.В. Бородич В.Н. Рыжик «Аналитическая геометрия » Тексты лекций Гомель, 2004 УДК 514 (078) ББК 22.151 Я73 Х 69
Рецензенты: Семенчук В.Н. – профессор, доктор физико-математических наук кафедра высшей математики учреждения образования «Гомельский государственный университет имени Франциска Скорины».
Рекомендован к изданию научно-методическим советом учреждения образования «Гомельский государственный университет имени Франциска Скорины» 24 марта 2004 года, протокол № 7
Ходалевич А.Д. Х 69 Аналитическая геометрия: Тексты лекций. /А.Д.Ходалевич, Р.В.Бородич, В.Н. Рыжик. − Гомель: УО «ГГУ им. Ф.Скорины»; 2004 − 65с.
Дается краткое изложение курса лекций по аналитической геометрии для студентов, обучающихся по специальности «Прикладная математика»
УДК 514 (078) ББК 22.151 Я73 Х 69
© А.Д. Ходалевич, Р.В. Бородич, В.Н. Рыжик, 2004 © Учреждение образования «Гомельский государственный университет имени Франциска Скорины», 2004
СОДЕРЖАНИЕ
1. Векторы и координаты………………………………….…4 2. Прямая на плоскости………………………………………20 3. Плоскость…………………………………………………...25 4. Прямая в пространстве. Взаимное расположение прямой и плоскости в пространстве…………………………29 5. Кривые второго порядка…………………………………...33 6. Поверхности второго порядка……………………………..56
Литература………………………………………………….….64
Аналитическая геометрия - это раздел математики, в котором геометрические объекты изучаются с помощью алгебраических методов, в основе которых лежит понятие координат. ВЕКТОРЫ И КООРДИНАТЫ Понятие вектора Пусть А – произвольное непустое множество. Декартовым кваратом А называется множество A2 = Бинарным отношением на А называется любое подмножество Отношением эквивалентности на А называется такое бинарное отношение 1) 2) если ( 3) если (
Теорема.Любое отношение эквивалентности на множестве А определяет разбиение этого множества на попарно непересекающиеся классы (классы эквивалентности). Обратно, любое разбиение множества А на попарно непересекающиеся классы определяет отношение эквивалентности на А.
Направленный отрезок – отрезок, у которого указано, какая точка является началом, а какая концом. Обозначается Пусть заданы направленные отрезки Если направленные отрезки Абсолютной величиной или модулем (длиной) направленного отрезка Два направленных отрезка
Теорема. Отношение равенства направленных отрезков является отношением эквивалентности.
Тогда вектором называется абстрактный объект, совпадающий с некоторым классом эквивалентности. Таким образом, каждый из равных друг другу направленных отрезков считается представлением (изображением) данного вектора, а неравные направленные отрезки считаются представлением разных векторов. Поэтому в дальнейшем вектор изображается точно так, как и соответствующий ему направленный отрезок.
Векторы Три и более векторов называются компланарными, если образующие их направленные отрезки параллельны некоторой плоскости. Нулевым вектором называется вектор, начало которого совпадает с его концом (обозначается
Линейные операции над векторами.
Определение. Суммой
Если имеется n векторов
Определение. Разностью векторов Легко показать, что для любого вектора что Определение. Произведением вектора 1) векторы 2) |
По определению, произведение произвольного вектора Введенные операции сложения векторов и умножение вектора на число называются линейными. Они обладают следующими свойствами: 1) сложение векторов коммутативно:
2) сложение векторов ассоциативно: ( 3) 4) 5) умножение вектора на число ассоциативно: α (β 6) 1 7) умножение вектора на число дистрибутивно по отношению к сложению чисел: (α+β) 8) умножение вектора на число дистрибутивно по отношению к сложению векторов: α( Множество всех векторов пространства (плоскости), удовлетворяющих свойствам 1) – 8), называется линейным, или векторным пространством, и обозначается
Теорема (необходимое и достатаочное условие коллинеарности двух векторов). Для того чтобы векторы
Проекции.
Назовем осью прямую, на которой указано направление, которое будем называть положительным.
Пусть l - некоторая ось, α - плоскость, непараллельная оси l. Через произвольную точку А пространства проведем плоскость α'||α и обозначим точку пересечения плоскости α' c осью l через А1. Тогда точка А1 называется проекцией точки А на ось l относительно плоскости α. В частности, если α
Пусть теперь задан вектор Тогда вектор а) | б) - | Обычно из контекста ясно о проекции относительно какой плоскости идет речь. Поэтому величину проекции вектора
Если прямая l Определение. Углом между двумя векторами, или между осями, или между вектором и осью называется наименьший угол α, на который надо повернуть один из векторов или одну из осей до совпадения по направлению с другим вектором или осью. Из определения следует, что 0
Теорема. Проекция вектора на ось обладает следуицики свойствами: 1) 2) 3)

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
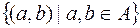
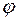 множества A2.
множества A2.
 (рефлексивность);
(рефлексивность); ,b)
,b)  то (b,
то (b,  (симметричность);
(симметричность); то (
то (  .
. , не лежащие на двух различных параллельных прямых, и плоскость
, не лежащие на двух различных параллельных прямых, и плоскость  , проходящая через точки В и D. Тогда плоскость
, проходящая через точки В и D. Тогда плоскость  ). В противном случае, они называются противоположно направленными (обозначается
). В противном случае, они называются противоположно направленными (обозначается  ).
). , который одинаково направлен с каждым из направленных отрезков
, который одинаково направлен с каждым из направленных отрезков 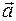 называется длина этого направленного отрезка и обозначается |
называется длина этого направленного отрезка и обозначается |  и
и  называются равными, если
называются равными, если  и
и  , при этом пишут
, при этом пишут  ). Направление нулевого вектора не определено.
). Направление нулевого вектора не определено. векторов
векторов 

 , то их сумма определяется как вектор
, то их сумма определяется как вектор  .
.

 =
=  .
. . Вектор, противоположный вектору
. Вектор, противоположный вектору 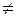 0) называется вектор
0) называется вектор  (
(  ).
). l, то проекция называется прямоугольной, или ортогональной.
l, то проекция называется прямоугольной, или ортогональной.

 называется проекциейвектора
называется проекциейвектора  Пусть α - некоторая плоскость и l – прямая, такая, что l не параллельна α. Через произвольную точку А пространства проведем прямую l1 || l и обозначим точку пересечения прямой l1 с плоскостью α через А1. Точка А1 называется проекциейточки А наплоскость α относительнопрямой l.
Пусть α - некоторая плоскость и l – прямая, такая, что l не параллельна α. Через произвольную точку А пространства проведем прямую l1 || l и обозначим точку пересечения прямой l1 с плоскостью α через А1. Точка А1 называется проекциейточки А наплоскость α относительнопрямой l. α
α  ), (
), (  ), (
), (  ).
).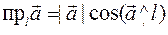 ;
;
 .
.