
|
|
Приложения линейной алгебры в произврдственно-экономических задачах международной торговлиПри анализе закупок товаров различных видов используются понятия собственного числа и собственного вектора матрицы. Предположим, что n стран расходуют х1,х2…хn бюджетов своих стран. Рассмотрим линейную модель обмена (модель международной торговли). Пусть аij – доля бюджета xj, котрую j страна расходует на закупку товаров у страны xi. Введем матрицу коэффициентов aij. Тогда если весь бюджет расходуется только на закупки внутри страны и вне ее (торговый бюджет), то справедливо равенство: сумма всех ij=1. Матрица А с последним свойством называется структурной матрицей торговли. Для i страны общая выручка от внутренней и внешней торговли выражается формулой: Pi = ai1x1+ai2x2+ainxn Условие сбалансированной (бездефицитной) торговли формулируется естественным образом: для каждой страны ее бюджет должен быть не больше выручки от торговли. Pi > или = Xi Можно доказать, что в последнем условии может быть только «=» Введем вектор бюджетов Х, каждая координата (компонента) которого характеризует бюджет соответствующей страны. Тогда можно записать систему линейных уравнений соответствующих условиям бездефицитной торговли Pi = Xi A11x1+a12x2+a1nxn=x1 A21x1+a22x2+a2nxn=x2 и т.д. Для определения вектора Х последнее уравнение можно переписать в виде (А-Е)Х=0 =>для бездефицитной торговли должно выполняться условие альфа=1 Пусть структурная матрица, т.е. матрица с неотрицательными элементами, а ее собственный вектор с положительными элементами имеет вид А= 0,2 0,3 0,2 0,2 0,4 0,3 0,1 0,2 0,3 0,3 0,5 0,2 0,1 0,1 0,2 0,4 Матрица дана для торговли 4-ех стран. Найти бюджет этих стран, которые удовлетворяют условию бездефицитной торговли (сбалансированной) при условии, что задана сумма бюджетов этих стран Х1+х2+х3+х4 = 6270 Составим матричное уравнение -0,8 0,3 0,2 0,2 х1 0 0,4 -0,7 0,1 0,2 * х2 = 0 Х3 0 Х4 0 Приведем матрицу к ступенчатому виду и составим систему уравнений Х1+х2+2х3-6х4=0 -11х2-7х3+26х4=0 -11х3+20х4=0 Найдем все значения х!!! Элементы аналитической геометрии на плоскости. Уравнение прямой в зависимости от параметра. Длина отрезка и деление отрезка в заданном соотношении.
Если точка М(x; y) лежит на прямой, проходящей через две данные точки
Если точка М является серединой отрезка
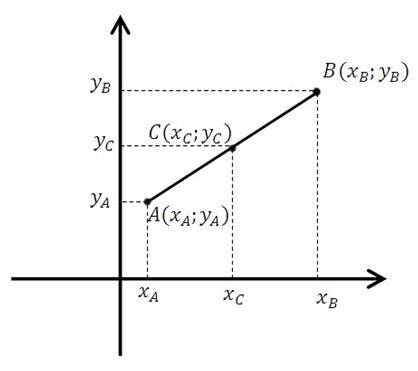
Длина отрезка на координатной плоскости. Формула для определения длины отрезка, если известны координаты его концов:
Координаты середины отрезка.
Пусть точка С является серединой отрезка АВ:
Формула для нахождения координат середины отрезка:
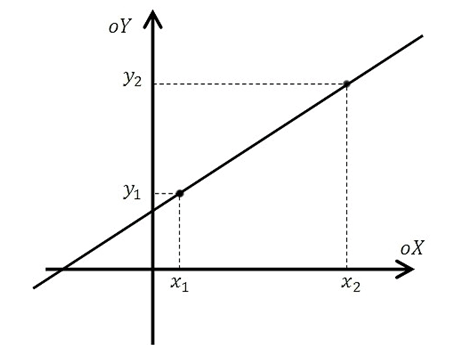
Уравнение прямой походящей через две данные точки.
Формула уравнения прямой походящей через две данные точки имеет вид:
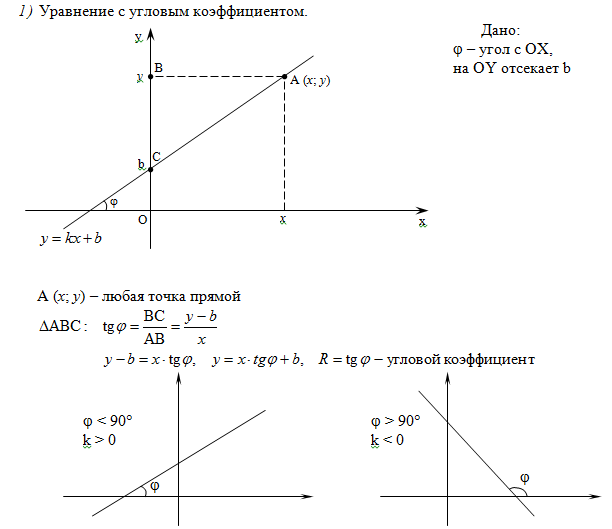
Подставив значения координат в формулу, она приводится к виду: y = kx + b, где k — это угловой коэффициент прямой Условия параллельности и перпендикулярности прямых и угол между ними. Расстояние от точки до прямой. Пусть на плоскости заданы две прямые:
Две прямые параллельны тогда и только тогда, когда их угловые коэффициенты равны, т.е. ,или . (7.1) Пример 1.Составить уравнение прямой, проходящей через точку Решение. Составим уравнение прямых, проходящих через точку
Выберем из этого пучка прямую, параллельную прямой
Ответ: Две прямые перпендикулярны тогда и только тогда, когда их угловые коэффициенты обратны по абсолютной величине и противоположны по знаку, т.е.
или
Пример 2.Составить уравнение прямой Решение. Составим уравнение прямых, проходящих через точку Найдем угловой коэффициент прямой то Отсюда Подставляя значение Ответ: Следует обратить внимание на то, что в числителе дроби из углового коэффициента второй прямой вычитается угловой коэффициент первой прямой. Если уравнения прямой заданы в общем виде A1x + B1y + C1 = 0, A2x + B2y + C2 = 0, (6) угол между ними определяется по формуле

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|



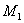 (
(  ,
,  ) и
) и  (
( 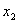 ,
, 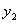 ), и дано отношение
), и дано отношение 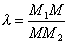 , в котором точка М делит отрезок
, в котором точка М делит отрезок  , то координаты точки М определяются по формулам
, то координаты точки М определяются по формулам ,
,  .
. ,
,  .
.
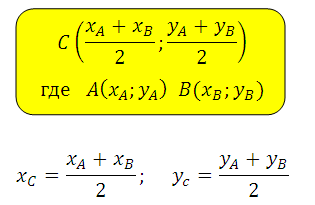
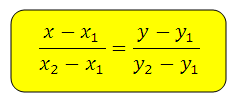
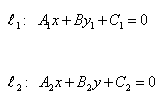
 параллельно прямой
параллельно прямой  .
. . (7.2)
. (7.2) . Для этого воспользуемся условием параллельности прямых. Так как ,то
. Для этого воспользуемся условием параллельности прямых. Так как ,то  .По формуле (3.7) имеем,
.По формуле (3.7) имеем,  . В формулу (7.2) подставим значение
. В формулу (7.2) подставим значение  :
:
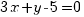 .
.
 (7.3)
(7.3) , проходящей через точку
, проходящей через точку  перпендикулярно прямой
перпендикулярно прямой 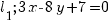 .
. . (7.4)
. (7.4)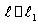
 .По формуле (3.7) вычислим
.По формуле (3.7) вычислим 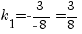 .
. .
. .
.


 (7)
(7)
