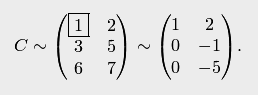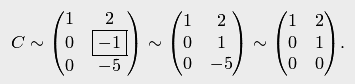|
|
Приведение матрицы к ступенчатому виду. Элементарные преобразования строк и столбцов.Матрица, виды матриц, действия над матрицами. Виды матриц: 1. Прямоугольные: m и n - произвольные положительные целые числа 2. Квадратные: m=n 3. Матрица строка: m=1. Например, (1 3 5 7 ) - во многих практических задачах такая матрица называется вектором 4. Матрица столбец: n=1. Например
5. Диагональная матрица: m=n и aij=0, если i≠j. Например
6. Единичная матрица: m=n и
7. Нулевая матрица: aij=0, i=1,2,...,m j=1,2,...,n
8. Треугольная матрица: все элементы ниже главной диагонали равны 0. Пример.
9. Симметрическая матрица:m=n и aij=aji(т.е. на симметричных относительно главной диагонали местах стоят равные элементы), а следовательноA'=A Например,
10. Кососимметрическая матрица: m=n и aij=-aji (т.е. на симметричных относительно главной диагонали местах стоят противоположные элементы). Следовательно, на главной диагонали стоят нули (т.к. при i=jимеем aii=-aii) Пример.
Действия над матрицами: 1. Сложение матриц - поэлементная операция
2. Вычитаниематриц - поэлементная операция
3. Произведение матрицы на число - поэлементная операция
4. Умножение A*B матриц по правилу строка на столбец (число столбцов матрицы А должно быть равно числу строк матрицы B) Amk*Bkn=Cmn причем каждый элемент сijматрицы Cmn равен сумме произведений элементов i-ой строки матрицы А на соответствующие элемеенты j-го столбца матрицы B , т.е.
Покажем операцию умножения матриц на примере
5. Транспонирование матрицы А. Транспонированную матрицу обозначают AT или A'
Строки и столбцы поменялись местами Свойства операций над матрицами: A+B=B+A (A+B)+C=A+(B+C) λ(A+B)=λA+λB A(B+C)=AB+AC (A+B)C=AC+BC λ(AB)=(λA)B=A(λB) A(BC)=(AB)C (A')'=A (λA)'=λ(A)' (A+B)'=A'+B' (AB)'=B'A'
2. Определители второго и третьего порядка (основные понятия, св-ва, вычисления)
Свойство 1. Определитель не изменяется при транспонировании, т.е.
Доказательство.
= Замечание. Следующие свойства определителей будут формулироваться только для строк. При этом из свойства 1 следует, что теми же свойствами будут обладать и столбцы.
Свойство 2. При умножении элементов строки определителя на некоторое число весь определитель умножается на это число, т.е.
Доказательство.
Свойство 3. Определитель, имеющий нулевую строку, равен 0. Доказательство этого свойства следует из свойства 2 при k = 0.
Свойство 4. Определитель, имеющий две равные строки, равен 0.
Доказательство. Свойство 5. Определитель, две строки которого пропорциональны, равен 0. Доказательство следует из свойств 2 и 4.
Свойство 6. При перестановке двух строк определителя он умножается на –1.
Доказательство.
Свойство 7.
Доказательство этого свойства можно провести самостоятельно, сравнив значения левой и правой частей равенства, найденные с помощью определения 1.5.
Свойство 8. Величина определителя не изменится, если к элементам одной строки прибавить соответствующие элементы другой строки, умноженные на одно и то же число.
Минор. Алгебраическое дополнение. Теорема Лапласа.
5. Приведение матрицы к ступенчатому виду. Элементарные преобразования строк и столбцов.
Метод приведения к треугольному виду заключается в таком преобразовании данного определителя, когда все элементы его, лежащие по одну сторону одной из его диагоналей, становятся равными нулю. Пример 8.Вычислить определитель Решение. Вычтем первую строку определителя из остальных его строк. Тогда получим Этот определитель равен произведению элементов главной диагонали. Таким образом, имеем Замечание. Всё рассмотренное выше можно обобщить для определителей n-го порядка. Приведение матрицы к ступенчатому виду. Элементарные преобразования строк и столбцов. Элементарными преобразованиями матрицы называются следующие ее преобразования: I. Перестановка двух столбцов (строк) матрицы. II. Умножение всех элементов одного столбца (строки) матрицы на одно и то же число, отличное от нуля. III. Прибавление к элементам одного столбца (строки) соответствующих элементов другого столбца (строки), умноженных на одно и то же число. Матрица Элементарные преобразования применяются для упрощения матриц, что будет в дальнейшем использоваться для решения разных задач. Чтобы привести матрицу к ступенчатому виду (рис. 1.4), нужно выполнить следующие действия. 1. В первом столбце выбрать элемент, отличный от нуля (ведущий элемент). Строку с ведущим элементом (ведущая строка), если она не первая, переставить на место первой строки (преобразование I типа). Если в первом столбце нет ведущего (все элементы равны нулю), то исключаем этот столбец, и продолжаем поиск ведущего элемента в оставшейся части матрицы. Преобразования заканчиваются, если исключены все столбцы или в оставшейся части матрицы все элементы нулевые. 2. Разделить все элементы ведущей строки на ведущий элемент (преобразование II типа). Если ведущая строка последняя, то на этом преобразования следует закончить. 3. К каждой строке, расположенной ниже ведущей, прибавить ведущую строку, умноженную соответственно на такое число, чтобы элементы, стоящие под ведущим оказались равными нулю (преобразование III типа). 4. Исключив из рассмотрения строку и столбец, на пересечении которых стоит ведущий элемент, перейти к пункту 1, в котором все описанные действия применяются к оставшейся части матрицы. Пример 1.29. Привести к ступенчатому виду матрицы
Решение. В первом столбце матрицы
Первый столбец и первую строку исключаем из рассмотрения. В оставшейся части матрицы имеется один элемент (-2), который выбираем в качестве ведущего. Разделив последнюю строку на ведущий элемент, получаем матрицу ступенчатого вида
В первом столбце матрицы
Пункт 3 алгоритма делать не надо, так как под ведущим элементом стоит нуль. Исключаем из рассмотрения первую строку и первый столбец. В оставшейся части ведущий элемент — число 2. Разделив ведущую строку (вторую) на 2, получаем ступенчатый вид:
Преобразования закончены, так как ведущая строка последняя. В первом столбце матрицы
Обратим внимание на то, что полученная матрица еще не является матрицей ступенчатого вида, так как вторую ступеньку образуют две строки (2-я и 3-я) матрицы. Исключив 1-ю строку и 1-й столбец, ищем в оставшейся части ведущий элемент. Это элемент (-1). Делим вторую строку на (-1), а затем к третьей строке прибавляем ведущую (вторую), умноженную на 5:
Исключим из рассмотрения вторую строку и второй столбец. Поскольку исключены все столбцы, дальнейшие преобразования невозможны. Полученный вид — ступенчатый. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

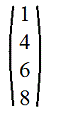
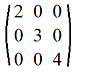
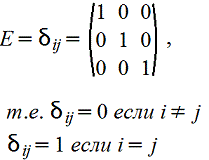
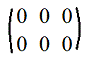
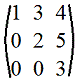
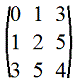
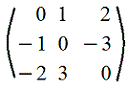
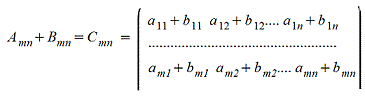
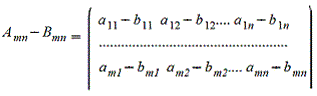
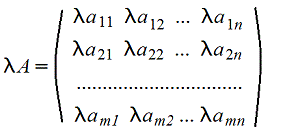
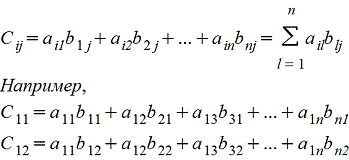
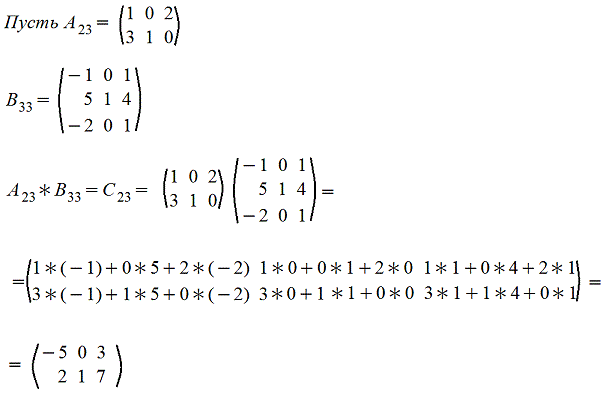
 ,например
,например 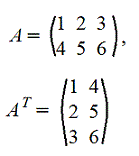







 .
.




















 приведением к треугольному виду.
приведением к треугольному виду.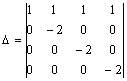 .
.
 , полученная из исходной матрицы
, полученная из исходной матрицы  конечным числом элементарных преобразований, называется эквивалентной. Это обозначается
конечным числом элементарных преобразований, называется эквивалентной. Это обозначается  .
.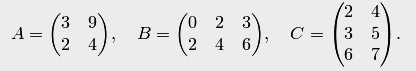
 . Делим все элементы первой строки на
. Делим все элементы первой строки на  (или, что то же 1 1. самое, умножаем на
(или, что то же 1 1. самое, умножаем на  ):
):
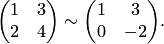
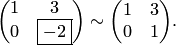
 . Меняем местами строки, ставя ведущую строку на место первой, и делим элементы ведущей строки на ведущий элемент 2:
. Меняем местами строки, ставя ведущую строку на место первой, и делим элементы ведущей строки на ведущий элемент 2: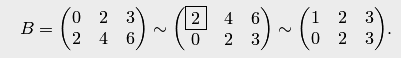
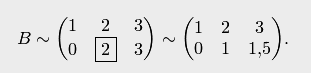
 выбираем ведущий элемент
выбираем ведущий элемент  . Первая строка — ведущая. Делим ее элементы на
. Первая строка — ведущая. Делим ее элементы на  . Получаем
. Получаем