|
Однородная система линейных уравнений. Фундаментальная система решений. Системы линейных уравнений в экономических задачах.
Однородной системойmлинейных уравнений сnнеизвестными называется система вида
| | | ì ï ï í ï ï î
| | a11x1 + a12x2 + … + a1nxn = 0
| | a21x1 + a22x2 + … + a2nxn = 0
| | … … … … … … … … … … …
| | am1x1 + am2x2 + … + amnxn = 0
| | | | | | (1)
| Эта система может быть записана в виде матричного уравнения
| A · X = O
| 1. Решить систему уравнений
 методом Гаусса. Решение. Выполним элементарные преобразования над строками матрицы коэффициентов, приведя ее к ступенчатому виду:
методом Гаусса. Решение. Выполним элементарные преобразования над строками матрицы коэффициентов, приведя ее к ступенчатому виду:
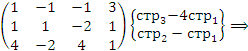  Ранг матрицы равен 3, тогда как число неизвестных равно 4. Поэтому одну из неизвестных, например,
Ранг матрицы равен 3, тогда как число неизвестных равно 4. Поэтому одну из неизвестных, например,  следует рассматривать как свободный параметр. Далее нужно присвоить этому параметру произвольное значение следует рассматривать как свободный параметр. Далее нужно присвоить этому параметру произвольное значение 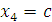 и выразить базисные неизвестные и выразить базисные неизвестные 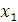 , , 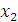 и и 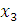 через c. Преобразованная матрица соответствует следующей системе уравнений: через c. Преобразованная матрица соответствует следующей системе уравнений:
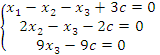 Из последнего уравнения следует, что
Из последнего уравнения следует, что 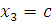 . Выразим остальные базисные переменные: . Выразим остальные базисные переменные:
 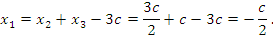 Таким образом, общее решение системы найдено:
Таким образом, общее решение системы найдено:
 Чтобы найти частное решение, нужно придать параметру c какое-нибудь числовое значение. Полагая c = 4, получаем
Чтобы найти частное решение, нужно придать параметру c какое-нибудь числовое значение. Полагая c = 4, получаем
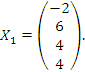 Проверка: Подставим неизвестные
Проверка: Подставим неизвестные
 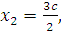 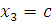 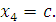 в уравнения системы:
в уравнения системы:
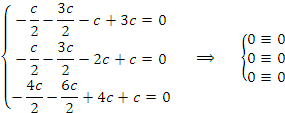 Уравнения обратились в тождества.
Уравнения обратились в тождества.
|
***
2. Пусть 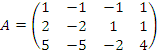 .
Найти общее решение однородной системы линейных уравнений AX = 0. Решение. Преобразуем коэффициентную матрицу к ступенчатому виду: .
Найти общее решение однородной системы линейных уравнений AX = 0. Решение. Преобразуем коэффициентную матрицу к ступенчатому виду:
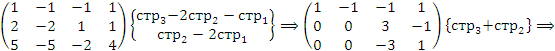  Поскольку
Поскольку  , а число неизвестных равно 4, то две неизвестные должны рассматриваться как базисные, а оставшиеся переменные как свободные параметры. Полагая , а число неизвестных равно 4, то две неизвестные должны рассматриваться как базисные, а оставшиеся переменные как свободные параметры. Полагая 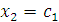 и и 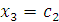 , получаем уклрлченную систему уравнений , получаем уклрлченную систему уравнений
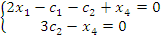 решение которой имеет вид
решение которой имеет вид
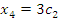 , ,  .
Запишем общее решение .
Запишем общее решение
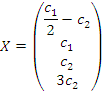 и представим его в виде линейной комбинации частных решений:
и представим его в виде линейной комбинации частных решений:
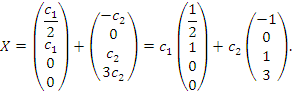 Если общее решение однородной системы представлено в виде линейной комбинации типа
Если общее решение однородной системы представлено в виде линейной комбинации типа
 то говорят, что частные решения
то говорят, что частные решения 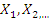 образуют фундаментальную систему решений.
В рассматриваемом случае фундаментальную систему решений образуют частные решения образуют фундаментальную систему решений.
В рассматриваемом случае фундаментальную систему решений образуют частные решения 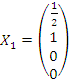 и и  . .
|
***
3. Предположим, что общее решение однородной системы уравнений имеет вид
 Очевидно, что
Очевидно, что
 и поэтому частные решения
и поэтому частные решения
 образуют фундаментальную систему решений.
образуют фундаментальную систему решений.
| Система линейных уравнений называется однородной, если все свободные члены уравнений равны нулю:
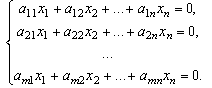
Однородная система всегда совместна, поскольку она всегда имеет тривиальное (нулевое) решение. Однако наибольший интерес представляют нетривиальные решения.
Теорема 1. Однородная система линейных уравнений имеет нетривиальное решение тогда и только тогда, когда ранг матрицы системы меньше числа неизвестных: r(A)=r<n.
Справедливо следующее утверждение: линейная комбинация решений однородной системы линейных уравнений также является ее решением.
Максимальная линейно независимая система решений называется фундаментальной системой решений однородной системы уравнений. Фундаментальная система решений содержит (n-r) векторов. Любое решение системы может быть представлено в виде линейной комбинации векторов фундаментальной системы решений.
Для нахождения фундаментальной системы решений нужно:
1) r базисных переменных выразить через свободные переменные;
2) выбрать линейно независимую систему (n-r) векторов (n-r)-мерного пространства (например, это могут быть единичные векторы);
3) поочередно заменить свободные переменные координатами векторов выбранной системы и вычислить значения базисных переменных.
Полученные решения  , , 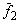 , …, , …, 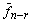 образуют фундаментальную систему решений. Тогда общее решение однородной системы уравнений имеет вид образуют фундаментальную систему решений. Тогда общее решение однородной системы уравнений имеет вид
 , ,
где 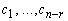 - произвольные числа. - произвольные числа.
ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ И ИХ ПРИМЕНЕНИЕ ПРИ РЕШЕНИИ ЭКОНОМИЧЕСКИХ ЗАДАЧ
В современной экономике используется множество математических методов, разработанных ещё в 20 веке. Применение линейной алгебры значительно упростило решение многих экономических задач. В данной работе рассматриваются основные способы решения задач с помощью элементов линейной алгебры.
Понятие матрицы и основанный на нем раздел математики – матричная алгебра – имеют большое значение для экономистов, основная часть математических моделей экономических объектов и процессов записывается в простой и компактной матричной форме. С помощью матриц удобно описывать различные экономические закономерности. Например, дана следующая таблица средних розничных цен на автомобили в зависимости от срока их службы (условных единиц).
| Продолжительность службы (годы)
| Годы
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| Предложенную таблицу можно записать в виде матрицы следующим образом:

где содержательное значение каждого показателя определяется его местом в матрице. К примеру, число 1825 во второй строке третьего столбца представляет собой цену прослужившего 2 года автомобиля в 2007 году. Аналогичным образом находим, что числа, записанные в строку, характеризуют цены автомобилей, прослуживших один и тот же срок в различные годы, а числа в столбце – цены автомобилей различного срока службы в данном году.
Таким образом, место, занимаемое числом в матрице, характеризует продолжительность использования автомобиля и год, к которому относится цена.
Применение матриц при решении экономических задач рассмотрим на следующем примере. Предприятие выпускает продукцию трех видов P1, P2, P3 и использует сырье двух типов: S1, S2. Нормы расхода сырья характеризуются матрицей:
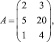
где каждый элемент aij (i = 1, 2, 3; j = 1,2) показывает, сколько единиц сырья j-го типа расходуется на производство единицы продукции i-го вида. План выпуска продукции задан матрицей-строкой C = (100 80 130).Стоимость единицы каждого типа сырья (денежных единиц) – матрицей-столбцом 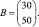 . Необходимо найти общую стоимость сырья. . Необходимо найти общую стоимость сырья.
Решение: Затраты первого сырья составляют S1 = 2∙100 + 5∙80 + 1∙130 = 730единиц, а второго S2 = 3∙100 + 2∙80 + 4∙130 = 980 единиц. Значит затраты сырья S могут быть записаны в виде матрицы строки (730 980) и произведения:
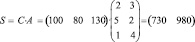
Общая стоимость сырья
Q = 730∙30 + 980∙50 = 70900 (денежных единиц)
может быть записана в следующем виде:
Q = S∙B = (CA)B = (70900).
Вывод: общая стоимость сырья составляет 70900.
Также экономические задачи можно решать с помощью систем линейных уравнений.
Рассмотрим и решим с помощью системы линейных уравнений следующую задачу:
Из определенного листового материала необходимо выкроить 360 заготовок типа А, 300 заготовок типа Б и 675 заготовок типа В. При этом можно применять три способа раскроя. Количество заготовок, получаемых из каждого листа при каждом способе раскроя, указано в таблице:
| Тип заготовки
| Способ раскроя
| |
|
|
| | А
|
|
|
| | Б
|
|
|
| | В
|
|
|
| Записать в математической форме условия выполнения задания.
Решение: Обозначим через x, y, z количество листов материала, раскраиваемых соответственно первым, вторым и третьим способами. Тогда при первом способе раскроя x листов будет получено 3 заготовок типа А, при втором – 2y, при третьем – z. Для полного выполнения задания по заготовкам типа А должно выполняться равенство:
 . .
Таким же способом получаем уравнения:
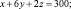 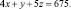
Имеем систему:
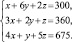
Данным уравнениям должны удовлетворять неизвестные x, y, z для того, чтобы выполнить задание по заготовкам Б и В. Полученная система линейных уравнений и выражает в математической форме условия выполнения всего задания по заготовкам А, Б и В.
Решим систему методом Гаусса.
1. Запишем систему в виде матрицы.
2. Составим расширенную матрицу системы.
3. Приведём полученную матрицу к треугольному виду.
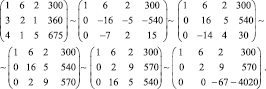
Исходная система равносильна следующей:
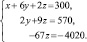
Решая полученную систему, имеем: x = 90, y = 15, z = 60.
Вывод: вектор C (90, 15, 60) есть решение системы.
Также, говоря, о роли линейной алгебры в экономике нельзя не упомянуть о модели многоотраслевой экономики Леонтьева, которая была разработана в виде математической модели в 1936 году. Эта модель основана на алгебре матриц и использует аппарат матричного анализа.
Рассмотрим задачу:
В таблице приведены коэффициенты прямых затрат и конечная продукция отраслей на плановый период, усл. ден. ед.
| Отрасль
| Потребление
| Конечный продукт
| | Промышленность
| Сельское хозяйство
| | Производство
| Промышленность
| 0,3
| 0,2
|
| | Сельское хозяйство
| 0,15
| 0,1
|
| Найти: плановые объёмы валовой продукции отраслей, межотраслевые поставки, чистую продукцию отраслей.
Решение:
1. Выпишем матрицу коэффициентов прямых затрат A, вектор конечной продукции Y:
 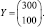
Заметим, что матрица A продуктивна, так как её элементы положительны и сумма элементов в каждом столбце меньше единицы.
2. Найдем матрицу
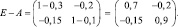
Тогда матрица полных затрат:
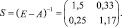
3. По формуле X = (E – A)–1⋅Y = SY найдем вектор валового продукта X:
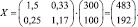
4. Межотраслевые поставки xij найдём по формуле xij = aij∙xj
X11 = a11∙x1 = 0,3·483 = 144,9;
X12 = 0,2·192 = 38,4;
X21 = 0,15·483 = 72,45;
X22 = 0,1·192 = 19,2.
5. Чистая продукция промышленности равна: 483 – 144,9 – 72,45 = 265,65
Чистая продукция сельского хозяйства: 192 – 38,4 – 19,2 = 134,4.
Итак, рассмотрев в данной статье некоторые задачи и их решения, можно сказать, что это лишь небольшая часть математических методов, используемых в экономике. Экономика и математика, очень тесно связаны и постепенно математические методы и модели начинают занимать очень важное место в экономике.
| 14.Векторы, основные понятия, действия над векторами в геометрической и координатной форме.
Основные определения.
Определение 1.Величина, полностью характеризуемая своим числовым значением в выбранной системе единиц, называется скалярной или скаляром.
(Масса тела, объем, время и т.д.)
Определение 2. Величина, характеризуемая числовым значением и направлением, называется векторной или вектором.
(Перемещение, сила, скорость и т.д.)
Обозначения: 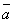 , , 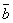 или или  , , 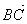 . .
Геометрический вектор – это направленный отрезок.
Для вектора  – точка А – начало, точка В – конец вектора. – точка А – начало, точка В – конец вектора.
Определение 3. Модульвектора – это длина отрезка AB.
Определение 4.Вектор, модуль которого равен нулю, называется нулевым, обозначается  . .
Определение 5.Векторы, расположенные на параллельных прямых или на одной прямой называются коллинеарными. Если два коллинеарных вектора имеют одинаковое направление, то они называются сонаправленными.
Определение 6.Два вектора считаются равными, если они сонаправлены и равны по модулю.
Действия над векторами.
Сложение векторов.
Опр. 6. Суммой двух векторов 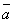 и и 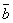 является диагональ параллелограмма, построенного на этих векторах, исходящая из общей точки их приложения (правило параллелограмма). является диагональ параллелограмма, построенного на этих векторах, исходящая из общей точки их приложения (правило параллелограмма).
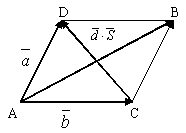
Рис.1.
Опр. 7.Суммойтрех векторов 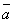 , , 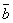 , , 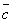 называется диагональ параллелепипеда, построенного на этих векторах (правило параллелепипеда). называется диагональ параллелепипеда, построенного на этих векторах (правило параллелепипеда).
Опр. 8.Если А, В, С – произвольные точки, то  + + 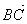 = = 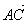 (правило треугольника). (правило треугольника).
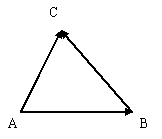
рис.2
Свойства сложения.
1о. 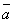 + + 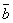 = = 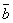 + + 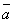 (переместительный закон). (переместительный закон).
2о. 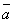 + ( + ( 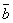 + + 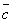 ) = ( ) = ( 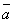 + + 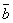 ) + ) + 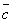 = ( = ( 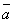 + + 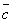 ) + ) + 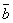 (сочетательный закон). (сочетательный закон).
3о. 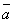 + (– + (– 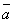 ) + ) +  . .
Вычитание векторов.
Опр. 9.Подразностью векторов 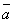 и и 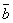 понимают вектор понимают вектор 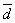 = = 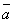 – – 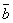 такой, что такой, что 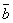 + + 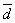 = = 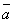 . .
В параллелограмме – это другая диагональ СД (см.рис.1).
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|


 методом Гаусса. Решение. Выполним элементарные преобразования над строками матрицы коэффициентов, приведя ее к ступенчатому виду:
методом Гаусса. Решение. Выполним элементарные преобразования над строками матрицы коэффициентов, приведя ее к ступенчатому виду:
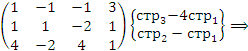
 Ранг матрицы равен 3, тогда как число неизвестных равно 4. Поэтому одну из неизвестных, например,
Ранг матрицы равен 3, тогда как число неизвестных равно 4. Поэтому одну из неизвестных, например,  следует рассматривать как свободный параметр. Далее нужно присвоить этому параметру произвольное значение
следует рассматривать как свободный параметр. Далее нужно присвоить этому параметру произвольное значение 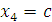 и выразить базисные неизвестные
и выразить базисные неизвестные 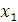 ,
, 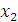 и
и 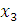 через c. Преобразованная матрица соответствует следующей системе уравнений:
через c. Преобразованная матрица соответствует следующей системе уравнений:
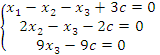 Из последнего уравнения следует, что
Из последнего уравнения следует, что 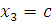 . Выразим остальные базисные переменные:
. Выразим остальные базисные переменные:

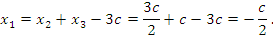 Таким образом, общее решение системы найдено:
Таким образом, общее решение системы найдено:
 Чтобы найти частное решение, нужно придать параметру c какое-нибудь числовое значение. Полагая c = 4, получаем
Чтобы найти частное решение, нужно придать параметру c какое-нибудь числовое значение. Полагая c = 4, получаем
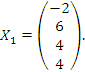 Проверка: Подставим неизвестные
Проверка: Подставим неизвестные

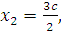
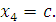 в уравнения системы:
в уравнения системы:
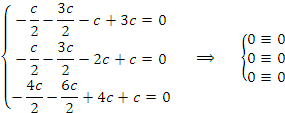 Уравнения обратились в тождества.
Уравнения обратились в тождества.
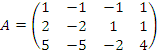 .
Найти общее решение однородной системы линейных уравнений AX = 0. Решение. Преобразуем коэффициентную матрицу к ступенчатому виду:
.
Найти общее решение однородной системы линейных уравнений AX = 0. Решение. Преобразуем коэффициентную матрицу к ступенчатому виду:
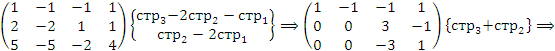
 Поскольку
Поскольку  , а число неизвестных равно 4, то две неизвестные должны рассматриваться как базисные, а оставшиеся переменные как свободные параметры. Полагая
, а число неизвестных равно 4, то две неизвестные должны рассматриваться как базисные, а оставшиеся переменные как свободные параметры. Полагая 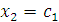 и
и 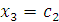 , получаем уклрлченную систему уравнений
, получаем уклрлченную систему уравнений
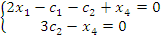 решение которой имеет вид
решение которой имеет вид
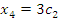 ,
,  .
Запишем общее решение
.
Запишем общее решение
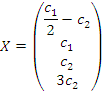 и представим его в виде линейной комбинации частных решений:
и представим его в виде линейной комбинации частных решений:
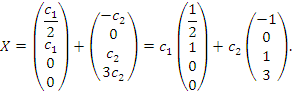 Если общее решение однородной системы представлено в виде линейной комбинации типа
Если общее решение однородной системы представлено в виде линейной комбинации типа
 то говорят, что частные решения
то говорят, что частные решения 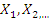 образуют фундаментальную систему решений.
В рассматриваемом случае фундаментальную систему решений образуют частные решения
образуют фундаментальную систему решений.
В рассматриваемом случае фундаментальную систему решений образуют частные решения 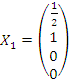 и
и  .
.
 Очевидно, что
Очевидно, что
 и поэтому частные решения
и поэтому частные решения
 образуют фундаментальную систему решений.
образуют фундаментальную систему решений.
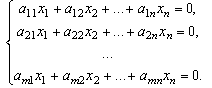
 ,
, 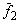 , …,
, …, 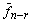 образуют фундаментальную систему решений. Тогда общее решение однородной системы уравнений имеет вид
образуют фундаментальную систему решений. Тогда общее решение однородной системы уравнений имеет вид ,
,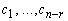 - произвольные числа.
- произвольные числа.
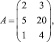
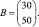 . Необходимо найти общую стоимость сырья.
. Необходимо найти общую стоимость сырья.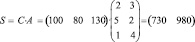
 .
.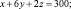
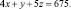
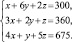
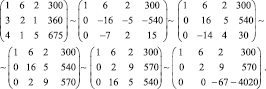
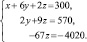

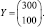
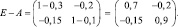
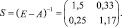
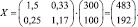
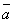 ,
, 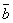 или
или  ,
, 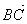 .
. – точка А – начало, точка В – конец вектора.
– точка А – начало, точка В – конец вектора. .
.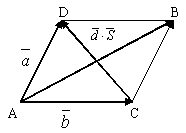
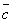 называется диагональ параллелепипеда, построенного на этих векторах (правило параллелепипеда).
называется диагональ параллелепипеда, построенного на этих векторах (правило параллелепипеда).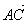 (правило треугольника).
(правило треугольника).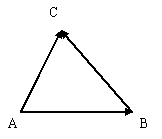
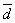 =
=