
|
|
Метод двойного предпочтенияВ случае больших размерностей, эффективен способ определения первоначального опорного плана с помощью метода двойного предпочтения. В каждом столбце отмечают знаком клетку с наименьшей стоимостью. Затем тоже проделывают в каждой строке. В результате некоторые клетки имеют двойную отметку. В них находится минимальная стоимость как по столбцу, так и по строке. В эти клетки помещают максимально возможные объемы перевозок, каждый раз исключая и рассмотрения соответствующие столбцы или строки. Затем распределяют перевозки по клеткам с единичной отметкой. Остальные перевозки распределяют по наименьшей стоимости. Пример
2. Заполняем клетки с простым предпочтением, начиная с наименьшей стоимости.
3. Заполняем оставшиеся пустыми клетки. Это опорный план составленный методом двойного предпочтения 4.4. Методы проверки опорного плана на оптимальность 4.4.1. Потенциалы. Критерий оптимальности плана Итак, наша транспортная задача имеет вид:
Распишем нашу задачу в векторной форме. Для этого введем векторы
Тогда ограничения задачи (3) могут быть записаны в виде
Как уже говорилось выше, одно из этих ограничений является лишним, и оно может быть вычеркнуто. Рассмотрим теперь двойственную задачу. Так как ограничений всего m + n, то и соответствующие переменные двойственной задачи обозначим так:
Величины Так как одно из ограничений является лишним, то на самом деле одного из потенциалов нет. Для сохранения симметрии всех формул и обозначений
Пусть теперь
Это и позволяет проверить оптимальность любого опорного плана. Сам алгоритм выглядит следующим образом:
Если это условие выполняется для всех наборов индексов i , j , для которых
Прежде, чем приводить пример, расскажем о том, как реализуется пункт 2 этого алгоритма, когда находятся потенциалы 1. Одна из величин 2. Затем рассматриваются уравнения вида
3. Для этих индексов
для тех
4. Далее повторяются пункты 2 (движение по строкам) и 3 (движение по столбцам), пока не определятся все потенциалы. Проиллюстрируем этот процесс примером, а заодно покажем форму записи результатов при ручном счете. Пример Пусть имеется три склада с запасами Таблица стоимостей перевозок
Построим исходный опорный план методом северо-западного угла. Он имеет вид
План имеет 6=3+4-1 компонент, поэтому он является невырожденным. Заметим, что для него транспортные расходы равны Заготовим матрицу размером Далее действуем следующим образом:
Таким образом, определились потенциалы всех пунктов - и складов и пунктов потребления. Теперь можно закончить заполнение этой таблицы, вписав в пустые клетки суммы
В ней жирным шрифтом помечены те Сравнивая с матрицей величин, Дельта-метод Рассмотрим алгоритм дельта-метода в общем виде:
а) для каждой нулевой строки минимальное значение б) минимальное приращение В случае а) производится непосредственное перераспределение потребности из избыточной строки в недостаточную в клетку отмеченного столбца, которой соответствует минимальное В случае б) составляются цепочки. Для построения цепочки в нулевой строке в отмеченном столбце находим клетку, для которой разность меньше минимального значение Составляем для каждой цепочки алгебраическую сумму приращения, считая их отрицательными, если они стоят в клетке, отмеченной знаком “-”, и положительными, если клетка отмечена знаком “+”. Если сумма больше минимального 5. Исключаем из рассмотрения отмеченные столбцы. Если занятая клетка избыточной строка стала незанятой или избыточной , то начинаем п.4. В противном случае продолжаем процесс до тех пор, пока все строки не превратятся в нулевые 4.5. Алгоритм улучшения плана Сформулируем теперь алгоритм перехода к новому опорному плану, дающему меньшее значение функции потерь. Прежде, чем формулировать его в общем виде, покажем его основные моменты на том примере, который мы начали рассматривать. Вспомним, что ограничения двойственной задачи соответствовали тому, что
У нас условие
Введение в базис вектора
Но теперь у нас нарушился баланс запасов и потребностей - получилось, что
Необходимо восстановить баланс запасов и потребностей. Для этого поступают следующим образом: по ненулевым компонентам плана перевозок(включая и компоненту q ) строят циклвида столбец - строка- столбец- строка- ...- строка (см. рисунок), который начинается и кончается на компоненте q. Теперь для восстановления баланса запасов и потребностей можно поступить очень просто: при движении по столбцу от имеющихся компонентов плана надо отнимать q, а при движении по строке - наоборот,прибавлять q. В результате получится следующий план перевозок, уже сохраняющий баланс запасов и потребностей:
С балансом всё в порядке, но теперь у нас стало В результате получится новый опорный план следующего вида
Вычисляя транспортные расходы для этого плана, мы получим Опишем этот процесс в общем виде. Итак, пусть для некоторой пары индексов
Исходя из клетки - такой цикл всегда может быть построен; - такой цикл единственный. Итак, пусть этот цикл имеет вид
Установим новый планперевозок вида
Все остальные компоненты плана перевозок, не входящие в цикл, остаются неизменными. Наконец, выберем q таким образом, чтобы одна из новых компонент плана обратилась в нуль, а все остальные остались положительными. Для этого q следует взять в виде
В результате получится новый опорный план. Покажем, что этот новый опорный план дает меньшее значение транспортных расходов, чем старый план. Так как компоненты плана, не входящие в цикл, не изменяются, то их можно не учитывать. Для ненулевых компонент исходного плана
Для нового плана перевозок мы имеем
Ну, а дальнейшее очевидно: надо повторять все итерации до тех пор, пока не будет получен оптимальный план. В силу конечности числа вершин допустимой области, это может быть сделано за конечное число шагов.J Закончим наш учебный пример. Одну итерацию мы уже проделали. Вторая итерация Определение потенциалов и проверка оптимальности плана. Обычно это совмещается в одной таблице и выглядит в виде таблицы, приведенной на следующей странице. Сначала в таблицу выписываются
Затем определяются потенциалы. Обычно это легко сделать в уме, двигаясь по строкам и столбцам. Затем оставшиеся клетки заполняются суммами соответствующих
Наконец, производится сравнение получившейся таблицы с таблицей
Этап 2 Из тех пар индексов, где В нашем случае эти преобразования имеют следующий вид:
В нашем случае
то есть на 15.3 единицы. Следующая итерация дается без пояснений. Третья итерация
В данном случае для всех клеток таблицы выполняется условие Для этого плана перевозок значение транспортных расходов
По сравнению с исходным планом, полученным методом северо-западного угла, транспортные расходы уменьшились на 17.3 единицы, то есть на 21%. Теперь мы в состоянии доказать одну интересную теорему ТеоремаЕсли все запасы Доказательство Действительно, вспомните, как строился исходный опорный план методом северо-западного угла. При этом применялась только одна арифметическая операция - операция вычитания. А при вычитании целых чисел всегда получаются только целые числа. Поэтому исходный опорный план целочисленный. При переходе к новому опорному плану применялись три операции: нахождение минимума из нескольких чисел (при определении q ), вычитание и сложение. В применении к целым числам эти операции всегда дают целые числа. Поэтому на любой итерации получающийся план является целочисленным, в том числе и оптимальный план. Теорема доказана. Снятие вырожденности Эпсилон-прием К сожалению, при решении транспортных задач, особенно тогда, когда Для борьбы с этим неприятным явлением существует очень простой прием, который, в качестве профилактики, рекомендуется применять всегда, когда запасы продукта на складах и потребности пунктов потребления - целые числа.
с некоторым e >0. Можно взять e конкретным, но достаточно малым числом, а можно просто оставить в алгебраическом виде как букву. Затем транспортная задача решается обычным путем, а в ответе просто полагается e =0, (или полученный результат округляется, если e было взято конкретным малым числом). Проиллюстрируем этот прием на конкретном примере. Пример Пусть матрица стоимостей перевозок имеет вид:
Заметьте, что в данном случае Чтобы снять намечающееся вырождение, будем решать задачу с теми же
Дальнейшее дается с минимальными пояснениями. Построение исходного опорного плана. Используя метод северо-западного угла, получим следующий исходный опорный план
Для этого плана значение функции потерь равно
Первая итерация Этап 1
План не является оптимальным. Отмечены те элементы, для которых
Этап 2 Строим цикл, находим q и переходим к новому опорному плану.
В данном случае Вторая итерация Этап 1 Находим потенциалы и проверяем оптимальность плана.
Полученный план снова не является оптимальным. Условие Цикл нарисован заранее. Этап 2
В данном случае Третья итерация Этап 1 Нахождение потенциалов и проверка на оптимальность. Соответствующая таблица приведена ниже. В данном случае для всех клеток таблицы выполнено условие Чтобы получить решение исходной задачи, надо положить e =0. Тогда мы получим:
Найденный оптимальный план имеет всего 4 компоненты, то есть он является вырожденным. Для него значение транспортных потерь равно
то есть значение транспортных издержек уменьшилось по сравнению с планом, построенным по методу северо-западного угла , на 4 единицы. или на 9.5% Подстановка Еще один прием для снятия вырожденности – 0-подстановка. Рассмотрим задачу План, составленный методом северо-западного угла имеет вид:
План является вырожденным. Рассмотрим таблицу, в которой указаны цены на перевозки, за исключением базисных компонент.
Удалим из рассмотрения клетки, при постановке в которые некоторых единиц возникает цикл.
На места, заполненные стоимостями, можно поставить некоторый объем единиц (в нашем случае 0 единиц). Выберем минимальную стоимость Теперь план приобретет вид.
Чтобы не путать нулевую базисную компоненту с обычными 0, обычный 0, полученный при вычислениях будем изображать План примет вид

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

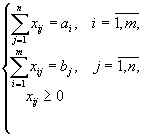



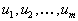 (переменные, соответствующие первым m ограничениям) и
(переменные, соответствующие первым m ограничениям) и  (переменные, соответствующие последним n ограничениям). Тогда, учитывая вид векторов
(переменные, соответствующие последним n ограничениям). Тогда, учитывая вид векторов  и вид вектора
и вид вектора 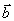 , запишем двойственную задачу в следующем виде:
, запишем двойственную задачу в следующем виде: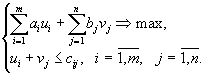
 называются потенциалами складов, а величины
называются потенциалами складов, а величины  - потенциалами пунктов потребления.
- потенциалами пунктов потребления. .
.
 - оптимальный опорный план транспортной задачи. Тогда, согласно теореме двойственности, должно выполняться условие
- оптимальный опорный план транспортной задачи. Тогда, согласно теореме двойственности, должно выполняться условие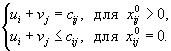
 для тех наборов индексов i , j , для которых
для тех наборов индексов i , j , для которых  , и находятся потенциалы
, и находятся потенциалы  ) проверяется условие
) проверяется условие 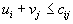 .
.
 ,
,
 задается произвольно, например, полагается
задается произвольно, например, полагается  для тех j , для которых
для тех j , для которых . Так как
. Так как 

 , которые больше нуля. Так как
, которые больше нуля. Так как  известны, тот находятся величины
известны, тот находятся величины 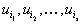 для некоторого множества индексов
для некоторого множества индексов  .
.
 и четыре пункта потребления с потребностями
и четыре пункта потребления с потребностями 
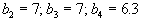 . Коэффициенты
. Коэффициенты  , определяющие стоимость перевозок, заданы матрицей:
, определяющие стоимость перевозок, заданы матрицей: .
.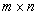 (в нашем случае размером 3´ 4), в которую впишем те коэффициенты
(в нашем случае размером 3´ 4), в которую впишем те коэффициенты 





 , следовательно
, следовательно 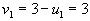 ;
;
 , следовательно
, следовательно  .
.
 , следовательно
, следовательно  .
.
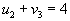 , следовательно
, следовательно  .
.
 , следовательно
, следовательно  .
.
 , следовательно
, следовательно  .
.
 , то есть суммы соответствующих потенциалов. В результате получим:
, то есть суммы соответствующих потенциалов. В результате получим: нарушено в двух местах - для
нарушено в двух местах - для 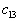 и
и  . Следовательно, построенный нами план перевозок не является оптимальным.
. Следовательно, построенный нами план перевозок не является оптимальным. , полученных соответственно в результате выбора каждого столбца наименьшей стоимости и вычитания ее из всех стоимостей столбца, а также таблицу
, полученных соответственно в результате выбора каждого столбца наименьшей стоимости и вычитания ее из всех стоимостей столбца, а также таблицу  , получающихся в результате выбора в каждой строке
, получающихся в результате выбора в каждой строке  , а выполнение условия
, а выполнение условия  говорило о том, что соответствующий вектор надо вводить в базис. Поэтому и выполнение
говорило о том, что соответствующий вектор надо вводить в базис. Поэтому и выполнение
 ,
,
 .
.
 ,
,
 .
.
 компонент плана, а должно быть
компонент плана, а должно быть  . Поэтому надо выбрать q так, чтобы одна из бывших компонент обратилась в нуль, но все остальные компоненты остались положительными. Легко догадаться, что для этого q надо взять равным минимальному из тех чисел, из которых q вычитается. В нашем случае q вычитается из чисел 2; 3.9; 2.8 . Минимальное из них есть 2 и поэтому надо взять q =2.
. Поэтому надо выбрать q так, чтобы одна из бывших компонент обратилась в нуль, но все остальные компоненты остались положительными. Легко догадаться, что для этого q надо взять равным минимальному из тех чисел, из которых q вычитается. В нашем случае q вычитается из чисел 2; 3.9; 2.8 . Минимальное из них есть 2 и поэтому надо взять q =2. , откуда видно, что по сравнению с исходным планом транспортные расходы уменьшилисьна 2 единицы.
, откуда видно, что по сравнению с исходным планом транспортные расходы уменьшилисьна 2 единицы. выполнено условие
выполнено условие  . Тогда вектор
. Тогда вектор  надо вводить в базис. Если таких векторов окажется несколько, то обычно вводят в базис тот вектор, для которого
надо вводить в базис. Если таких векторов окажется несколько, то обычно вводят в базис тот вектор, для которого


 ,
, .
.





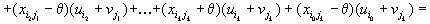


 , так что новый опорный план нарисован в таблице справа. Значение транспортных расходов уменьшилось на величину
, так что новый опорный план нарисован в таблице справа. Значение транспортных расходов уменьшилось на величину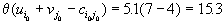 ,
, .
.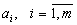 и все потребности
и все потребности  целые числа, то оптимальный план перевозок тоже целочисленный.
целые числа, то оптимальный план перевозок тоже целочисленный.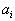 и
и 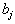 - целые числа, часто приходится сталкиваться с вырожденными опорными планами, то есть с планами, число положительных компонент которых меньше
- целые числа, часто приходится сталкиваться с вырожденными опорными планами, то есть с планами, число положительных компонент которых меньше  . Это бывает тогда, когда, как уже указывалось выше, какое-то подмножество складов удовлетворяет потребности какого-то подмножества пунктов потребления.
. Это бывает тогда, когда, как уже указывалось выше, какое-то подмножество складов удовлетворяет потребности какого-то подмножества пунктов потребления. ,
,


 .
.
 .
.
 , или
, или 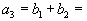
 , то есть имеются подгруппы складов, полностью удовлетворяющие потребности некоторых пунктов потребления.
, то есть имеются подгруппы складов, полностью удовлетворяющие потребности некоторых пунктов потребления.

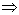
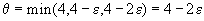 . Обратите внимание на то, что если бы было e =0, то построенный план имел бы всего 4 положительных компоненты, то есть он был бы вырожденным.
. Обратите внимание на то, что если бы было e =0, то построенный план имел бы всего 4 положительных компоненты, то есть он был бы вырожденным. . Опять-таки, если бы было e =0, то план был бы вырожденным.
. Опять-таки, если бы было e =0, то план был бы вырожденным.
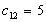 и поставим нулевую перевозку
и поставим нулевую перевозку  .
. .
.