
|
|
Постановка двойственных задачСимметричные двойственные задачи Рассмотрим задачу линейного программирования в стандартной форме
или, в матричной форме,
Рассмотрим теперь следующую задачу
или, в матричной форме,
Пара задач (1) и (3) (или, в матричной форме, пара задач (2) и (4) ) называются двойственнымидруг другу задачами в симметричной форме.
Несимметричная двойственная задача Исходная задачаимеет вид:
или, в матричной форме,
Двойственная задача в несимметричной форме имеет вид
или, в матричной форме,
Обратите внимание на то, что в несимметричной двойственной задаче не накладывается условие неотрицательности переменных. Если исходная задача линейного программирования записана в произвольной форме, то для записи двойственной задачи следует сначала записать исходную задачу в канонической или стандартной форме, а затем выписать двойственную задачу. При желании, получившуюся двойственную задачу также можно привести к какой-либо нестандартной форме. Экономическая интерпретация двойственной задачи в симметричной форме Исходная задача: Обычно эта задача связывается с задачей максимизации дохода при производстве некоторой продукции при наличии ограничений на ресурсы. Коэффициенты Целевая функция двойственной задачи: а ограничения: · (3) — запасы i-го ресурса; · (4) — стоимость единицы i-го ресурса; · (5) — общая стоимость всех ресурсов; · (6) — запасы i-го ресурса на производство единицы продукции j-го типа; · (7) — цена единицы i-го ресурса;
Таким образом, задачи симметричной двойственной пары могут быть сформулированы так. 1. Исходная задача. Сколько единиц
Переменные Свойства двойственных задач Полная теория двойственных задач очень сложна. Мы докажем часть соответствующих теорем в упрощенном варианте. Теорема 1. Для пары двойственных задач верно соотношение
Доказательство. Мы дадим доказательство в двух вариантах - для симметричной и для несимметричной пар двойственных задач. Симметричная пара Итак, пусть имеется симметричная пара двойственных задач, записанная в матричной форме:
Транспонируя систему ограничений второй задачи
получим, что
С другой стороны, из ограничений первой задачи, имеем
Поэтому
Но комбинация
А теперь можно написать следующую цепочку неравенств
2. Несимметричная пара Доказательство в этом случае почти дословно повторяет предыдущее. Итак, пусть имеется несимметричная пара двойственных задач в матричной записи
Транспонируя систему ограничений второй задачи
получим, что
С другой стороны, из ограничений первой задачи, имеем
Поэтому
Как и в предыдущем случае верно соотношение
Так как переменные
Теорема доказана. Следствие 1. Если в одной задаче из пары двойственных задач целевая функция неограничена, то во второй задаче допустимая область пуста. Доказательство.
что для любого допустимого плана
Следствие 2.Если для планов
то они являются оптимальными планами соответствующих задач. Доказательство. Действительно, пусть

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
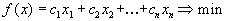

 ,
,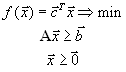
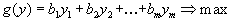

 ,
,
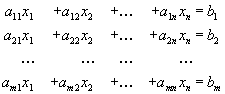
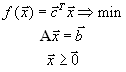
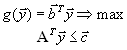

 имеют смысл дохода от единицы продукции j-го ресурса,
имеют смысл дохода от единицы продукции j-го ресурса,  — количество единиц продукции j-го вида. Коэффициенты
— количество единиц продукции j-го вида. Коэффициенты  имеют смысл затрат i-го ресурса на производство продукции j-го типа. Что же представляет двойственная задача по своему смыслу?
имеют смысл затрат i-го ресурса на производство продукции j-го типа. Что же представляет двойственная задача по своему смыслу?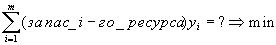 ,
,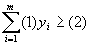 , где (1) — затраты i-го ресурса на производство единицы продукции j-го типа, а (2) — доход от продажи единицы продукта i-го типа. Поэтому в целевой функции на месте (?)получаем смысл стоимости всех ресурсов, т. е. Задача приобретает смысл:
, где (1) — затраты i-го ресурса на производство единицы продукции j-го типа, а (2) — доход от продажи единицы продукта i-го типа. Поэтому в целевой функции на месте (?)получаем смысл стоимости всех ресурсов, т. е. Задача приобретает смысл: 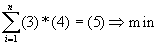 , при ограничениях:
, при ограничениях: 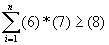 , где
, где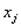 продукции каждого вида
продукции каждого вида  надо выпустить при доходе
надо выпустить при доходе  от продукции единицы j-го типа при имеющихся запасах каждого из ресурсов
от продукции единицы j-го типа при имеющихся запасах каждого из ресурсов 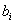 , чтобы получить максимальный доход?
, чтобы получить максимальный доход? от производства единицы каждого вида продукции минимизировать стоимость затрат?
от производства единицы каждого вида продукции минимизировать стоимость затрат?  называется по-разному. Часто их называют учетными, неявными или фиктивными ценами.
называется по-разному. Часто их называют учетными, неявными или фиктивными ценами.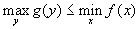 .
.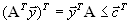
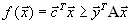 .
.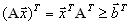 .
.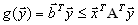 .
.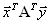 - это число, которое от транспонирования не меняется:
- это число, которое от транспонирования не меняется: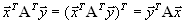 .
.
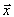 и
и 
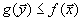 .
.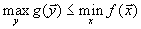 .
.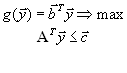
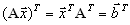 .
. .
.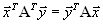 , так что для
, так что для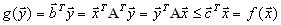
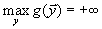 .
.
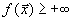 , что бессмысленно. Это означает, что допустимых планов не существует вообще.
, что бессмысленно. Это означает, что допустимых планов не существует вообще.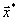 и
и 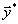 исходной и двойственной задач выполняется соотношение
исходной и двойственной задач выполняется соотношение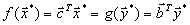 ,
,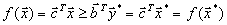 ,
,