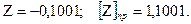|
|
Метод ускоренного сложения двоичных чиселС запоминанием переносов Для минимизации времени сложения при выполнении операций, требующих ряда последовательных суммирований большого количества чисел, в ряде случаев используют параллельные сумматоры с запоминанием переноса. В подобных сумматорах сложение выполняется как разрядная операция с запоминанием поразрядного значения суммы Siп Процесс ускоренного сложения с запоминанием переносов группы чисел состоит из ряда циклов по числу Для иллюстрации описанного метода рассмотрим пример сложения четырех чисел В последнем цикле вычисления суммы включается цепь переноса, по которой осуществляются межразрядные связи в сумматоре и формируется окончательный результат. Таблица 2.1
Из рассмотренного примера ясно, что использование принципа поразрядного сложения с запоминанием переносов при суммировании большого массива цифр, как это имеет место при выполнении экономических расчетов, операции умножения и деления, позволяет значительно сократить общее время суммирования за счет исключения времени на распространение переноса. Умножение двоичных чисел с фиксированной запятой Умножение двоичных чисел чаще всего осуществляется в прямом коде. Знак произведения определяется путем сложения по модулю два знаков сомножителей, что полностью соответствует известным правилам алгебры.
Определение знака Правило знаков произведения при умножении 0 0 1 1
Умножение сомножителей в прямом коде осуществляется по обычным правилам двоичной арифметики, изложенным выше. При этом умножение можно начинать как со старшего, так и с младшего разряда множителя. В первом случае каждое последующее частичное произведение сдвигается относительно предыдущего на один разряд вправо и суммируется с ним, а во втором случае очередное частичное произведение сдвигается влево на один разряд и также суммируется с предшествовавшей суммой частичных произведений. Частичные произведения, равные нулю, т.е. получающиеся умножением множимого на нулевое значение соответствующего разряда множителя, можно опускать, но сдвиг на один разряд равного нулю частичного произведения необходимо учитывать. Из сказанного следует, что умножение сомножителей фактически сводится к сдвигам (вправо или влево) множимого и сложению сдвинутых частичных произведений с предшествующей суммой частичных произведений. Известно, что количество разрядов произведения должно равняться сумме разрядов сомножителей. Поэтому при работе с фиксированной (постоянной) длиной разрядной сетки результат перемножения сомножителей должен ограничиваться по числу разрядов и округляться по известным в арифметике правилам.
Пример. Множимое Множитель Требуется найти Первый шаг.Определение знака произведения.
Второй шаг.Определение цифровой части (модуля) произведения
1011 1011
  1101 1101 1101 1101
1101 1101 1101 1101
Третий шаг.Ограничение результата четырьмя разрядами и округление 1001. Результат операции умножения

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 . Возникающие при этом в процессе последовательных сложений единичные сигналы переноса
. Возникающие при этом в процессе последовательных сложений единичные сигналы переноса  не распространяются по сумматору, а запоминаются в отдельном регистре переносов РП.
не распространяются по сумматору, а запоминаются в отдельном регистре переносов РП. слагаемых. В каждом цикле, за исключением последнего
слагаемых. В каждом цикле, за исключением последнего  -го, производится поразрядное сложение и формирование переносов трех чисел: очередного слагаемого, поразрядной суммы от предшествовавших сложений и значение переноса, сформированного в предшествующем цикле сложения. Образующиеся при этом новое поразрядное значение суммы и значение переноса запоминаются и в следующем цикле сложения суммируются с очередным слагаемым аналогичным образом. Для завершения выполнения сложения и получения окончательного результата (полной суммы) необходимо в последнем цикле выполнить операцию полного сложения с учетом распространения переноса, например, по цепи сквозного переноса.
-го, производится поразрядное сложение и формирование переносов трех чисел: очередного слагаемого, поразрядной суммы от предшествовавших сложений и значение переноса, сформированного в предшествующем цикле сложения. Образующиеся при этом новое поразрядное значение суммы и значение переноса запоминаются и в следующем цикле сложения суммируются с очередным слагаемым аналогичным образом. Для завершения выполнения сложения и получения окончательного результата (полной суммы) необходимо в последнем цикле выполнить операцию полного сложения с учетом распространения переноса, например, по цепи сквозного переноса.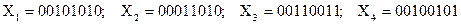 с запоминанием переноса
с запоминанием переноса  (табл. 2.1).
(табл. 2.1).

 S0,П
S0,П

 окончательный результат
сложения
окончательный результат
сложения

 .
.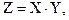 т.е. найти
т.е. найти  .
. .
.
 10001111 10001111
10001111 10001111