
|
|
Этап 4. Указание диапазона.В появившемся диалоговом окне Мастер диаграмм (шаг 2 из 4): Источник данных диаграммы необходимо выбрать вкладку Диапазон данных и в поле Диапазон мышью указать интервал данных В2:N22. Далее необходимо указать в строках или столбцах расположены ряды данных. Это определит ориентацию осей х и у. В примере переключатель Ряды в с помощью указателя мыши установим в положение столбцах. Этап 5. Ввод подписей по оси X. Выбираем вкладку Ряд и в поле Подписи оси X указываем диапазон подписей. Для этого следует активизировать данное поле, щелкнув в нем указателем мыши, и ввести в него диапазон подписей оси х — А2:А22. Вводим значения подписей оси у. Для этого в рабочем поле Ряд выбираем первую запись Ряд1 и в рабочее поле Имя, активизировав его указателем мыши, вводим значение первой переменной у В1. Затем в поле Ряд выбираем вторую запись — Ряд2 и в рабочее поле Имя вводим второе значение переменной у С1. Повторяем таким образом до последней записи — Ряд13. После появления требуемых записей необходимо нажать кнопку Далее.
Рис. 7. Диаграмма верхней части двуполостного гиперболоида Этап 6. Введение заголовков. В третьем окне требуется ввести заголовок диаграммы и названия осей. Для этого необходимо выбрать вкладку Заголовки, щелкнув на ней указателем мыши. Щелкнув в рабочем поле Название диаграммы указателем мыши, ввести с клавиатуры в поле название: Двуполостный гиперболоид. Затем аналогичным образом ввести в рабочие поля Ось X (категорий) и Ось Y (рядов данных), Ось Z(значений) соответствующие названия: ось OX, ось OY, ось OZ. Если внешний вид диаграммы нас устраивает, то необходимо нажать кнопку Далее. В противном случае нажать кнопку Назад и внести необходимые изменения на нужном этапе. Этап 7. Завершение. В четвертом окне Мастер диаграмм (шаг 4 из 4) требуется выбрать место расположения диаграммы на отдельном листе Диаграмма1 или имеющемся Лист1. По умолчанию переключатель будет стоять «имеющемся Лист1». В нашем случае оставляем по умолчанию. Нажимаем кнопку Готово. На текущем листе должна появиться следующая диаграмма (рис. 7). Этап 8. Переименование листа. Навести курсор на закладку Лист1, правой клавишей мыши (ПКМ) вызвать контекстное меню, выбрать пункт Переименовать, удалить старое название листа и с клавиатуры набрать новое Дв_гиперболоид, нажать Enter.
Задание 6. Построить верхнюю часть однополосного гиперболоида Задание 7. Построить верхнюю часть двухполостного гиперболоида
Эллипсоид Эллипсоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением:
Это уравнение называется каноническим уравнением эллипсоида. Эллипсоид представляет собой замкнутую овальную поверхность, обладающую тремя взаимно перпендикулярными плоскостями симметрии. Для построения эллипсоида в Ехсеl каноническое уравнение (8) необходимо разрешить относительно переменной z (представить в виде z=f(x,y)). Задание 8. Построить верхнюю часть эллипсоида
Параболоид Существует два вида параболоидов: эллиптические и гиперболические. Эллиптическим параболоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением:
Эллиптический параболоид имеет вид бесконечной выпуклой чаши. Он обладает двумя взаимно перпендикулярными плоскостями симметрии. Точка, с которой совмещено начало координат, называется вершиной эллиптического параболоида; числа р и q называются его параметрами. Гиперболическим параболоидом называется поверхность, определяемая уравнением
Гиперболический параболоид имеет форму седла. Он обладает двумя взаимно перпендикулярными плоскостями симметрии. Точка, с которой совмещено начало координат, называется вершиной гиперболического параболоида: числа р и q называются его параметрами. Задание 9. Построить эллиптический параболоид Задание 10. Построить гиперболический параболоид
Конус второго порядка
Конусом второго порядка называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением
Конус образован прямыми линиями (образующими), проходящими через начало координат (вершина конуса). Сечение конуса плоскостью, не проходящей через начало координат, дает эллипс. В Ехсе1 построение конуса второго порядка аналогично построению других поверхностей, рассмотренных ранее. Задание 11. Построить нижнюю часть конуса
Лабораторная работа №3 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

 , лежащую в диапазонах: хÎ[-10; 10] с шагом h=0.5, yÎ[-5; 5] с шагом h=0.25.
, лежащую в диапазонах: хÎ[-10; 10] с шагом h=0.5, yÎ[-5; 5] с шагом h=0.25. , лежащую в диапазонах: хÎ[-10; 10] с шагом h=0.5, yÎ[-5; 5] с шагом h=0.25.
, лежащую в диапазонах: хÎ[-10; 10] с шагом h=0.5, yÎ[-5; 5] с шагом h=0.25. . (8)
. (8) , лежащую в диапазонах: хÎ[-4; 4], yÎ[-3; 3] с шагом h=0.5 для обеих переменных.
, лежащую в диапазонах: хÎ[-4; 4], yÎ[-3; 3] с шагом h=0.5 для обеих переменных. . (9)
. (9)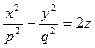 . (10)
. (10) . Диапазон изменения переменных: хÎ[-15; 15] с шагом h=0.5, yÎ[-5; 5] с шагом h=1.
. Диапазон изменения переменных: хÎ[-15; 15] с шагом h=0.5, yÎ[-5; 5] с шагом h=1. . Диапазон изменения переменных: хÎ[-10; 10] с шагом h=0.5, yÎ[-5; 5] с шагом h=1.
. Диапазон изменения переменных: хÎ[-10; 10] с шагом h=0.5, yÎ[-5; 5] с шагом h=1. . (11)
. (11) . Диапазон изменения переменных: хÎ[-10; 10] с шагом h=0.5, yÎ[-7; 7] с шагом h=1.
. Диапазон изменения переменных: хÎ[-10; 10] с шагом h=0.5, yÎ[-7; 7] с шагом h=1.