
|
|
Этап 4. Указание диапазона.В появившемся диалоговом окне Мастер диаграмм (шаг 2 из 4): источник данных диаграммы необходимо выбрать вкладку Диапазон данных и в поле Диапазон указать интервал данных. Для этого с помощью клавиши Delete необходимо очистить рабочее поле Диапазон и, убедившись, что в нем остался только мигающий курсор, навести указатель мыши на левую верхнюю ячейку данных (В2), нажать левую кнопку мыши и не отпуская ее, протянуть указатель мыши к правой нижней ячейке, содержащей выносимые на диаграмму данные (С34), затем отпустить левую кнопку мыши. Выделится диапазон B2:C34. Далее необходимо указать в Строках или Столбцах расположены ряды данных. Переключатель Ряды в с помощью указателя мыши следует установить в положение столбцах (черная точка должна стоять около слова Столбцах).
Этап 5. Ввод подписей по оси X. В диалоговом окне Мастер диаграмм (шаг 2 из 4): источник данных диаграммы необходимо выбрать вкладку Ряд (щелкнув на ней указателем мыши) и в поле Подписи оси X указать диапазон подписей (в примере — Аргумент). Для этого следует активизировать поле Подписи оси X, щелкнув в нем указателем мыши, и, наведя указатель мыши на левую верхнюю ячейку подписей (А2), нажать левую кнопку мыши и, не отпуская ее, протянуть указатель мыши к нижней ячейке, содержащей выносимые на ось X подписи (А34), затем отпустить левую кнопку мыши. В окне ввода появится диапазон А2:А34. Нажать кнопку Далее.
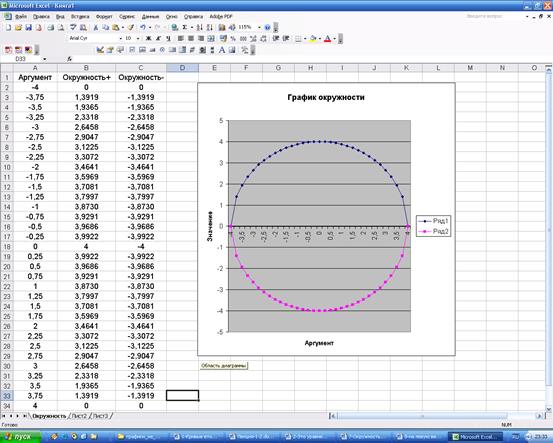
Рис. 1. Диаграмма окружности
Этап 6. Введение заголовков. В третьем окне Мастер диаграмм (шаг 3 из 4): параметры диаграммы требуется ввести заголовок диаграммы и названия осей. Для этого необходимо выбрать вкладку Заголовки, щелкнув на ней указателем мыши. Щелкнув в рабочем поле Название диаграммы указателем мыши, ввести с клавиатуры в поле название: График окружности. Затем аналогичным образом ввести в рабочие поля Ось X (категорий) и Ось Y (значений) соответствующие названия: Аргумент и Значения. Если внешний вид диаграммы в окне Предварительного просмотра нас устраивает, то необходимо нажать кнопку Далее. В противном случае нажать кнопку Назад и внести необходимые изменения на нужном этапе. Этап 7. Завершение. В четвертом окне Мастер диаграмм (шаг 4 из 4) требуется выбрать место расположения диаграммы на отдельном листе Диаграмма1 или имеющемся Лист1. По умолчанию переключатель будет стоять «имеющемся Лист1». В нашем случае оставляем по умолчанию. Нажимаем кнопку Готово. На текущем листе должна появиться следующая диаграмма (рис. 1). Этап 8. Переименование листа. Навести курсор на закладку Лист1, правой клавишей мыши (ПКМ) вызвать контекстное меню, выбрать пункт Переименовать, удалить старое название листа и с клавиатуры набрать новое Окружность, нажать Enter.
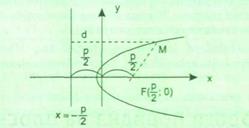
Парабола Параболой называется множество всех точек, расстояния от которых до данной точки, называемой фокусом, и до данной прямой, называемой директрисой, равны (рис.2). Уравнение параболы получается из уравнения кривой второго порядка (1). Если коэффициент В = О, а также один из коэффициентов А или С равен нулю, для определенности пусть А = О, С ¹ 0, то есть: Су2 + Dx + Ey + F = 0. (3) Это уравнение параболы с осью симметрии, перпендикулярно оси ординат. При А≠0, С=0 получим: Ax2+Dx + Ey + F = 0. (4) В данном случае это — уравнение параболы с осью симметрии, перпендикулярной оси абсцисс. Уравнения (3) и (4) представляют собой общие уравнения параболы. Каноническими уравнениями параболы являются: у2 = 2рх, где р — параметр параболы, расстояние от фокуса до директрисы, для кривой с горизонтально расположенной осью; х2 = 2ру — для параболы с вертикально расположенной осью. Схематичное изображение параболы представлено на рис.2.
Рис. 2. Схематическое изображение параболы Для построения параболы в MS Excel уравнение параболы должно быть приведено к виду y=f(x) (разрешено относительно переменной y). Построение диаграммы параболы осуществляется по тем же шагам, что и построение окружности. Задание 1. Построить параболу x2=12y в диапазоне x Î [-4; 4] с шагом h = 0.5 Задание 2. Построить параболу y2=8x в диапазоне x Î [-4; 4] с шагом h = 0.5
Гипербола
Кривая второго порядка (1) называется гиперболой, если коэффициенты A и С имеют противоположные знаки, то есть АС < 0. Характеристическое свойство гиперболы выражается в том, что она является множеством точек, разность расстояний от которых до двух данных точек Каноническое уравнение гиперболы имеет вид:
Здесь с — расстояние от начала координат до фокусов, а — расстояние от начала координат до вершин гиперболы.
Рис. 3. Схематическое изображение гиперболы В простейшем случае уравнение гиперболы имеет вид Задание 3. Построить гиперболу Задание 4. Построить гиперболу
Эллипс Кривая второго порядка (1) называется эллипсом, если коэффициенты A и С имеют одинаковые знаки, то есть АС > 0. Если коэффициент В также равен нулю, то это эллипс с осями, параллельными координатным осям. Если, кроме того, коэффициенты D = Е = 0, то центр эллипса находится в начале координат. Обычно в качестве определения эллипса используют его характеристическое свойство: эллипсом называется множество точек плоскости, сумма расстояний от которых до двух данных, называемых фокусами, есть величина постоянная, большая расстояния между фокусами. Каноническое уравнение эллипса может быть получено из его определения. Обозначим постоянную сумму расстояний от фокусов до точек эллипса 2а, а расстояние между фокусами — 2с. Систему координат введем следующим образом: ось х проходит через фокусы, ось у — через середину отрезка F1F2 (рис. 4).
Рис. 4. Расположение фокусов и точки на эллипсе (a>c)
Каноническое уравнение эллипса Эксцентриситетом эллипса называется величина Так как а>с, то
Рис. 5. Схематичное изображение эллипса Построение эллипса в MS Excel аналогично построению окружности. Задание 5. Построить эллипс Лабораторная работа №2 Цель работы: закрепить полученные знания при выполнении лабораторной работы №1. Научится использовать абсолютные ссылки, строить Поверхности второго порядка в пространстве. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
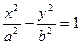
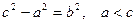
 — эксцентриситет,
— эксцентриситет, — асимптоты гиперболы.
— асимптоты гиперболы.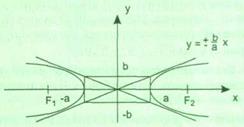
 .
. для x Î [-10; 10]. Шаг рассчитать самостоятельно, количество точек разбиения отрезка n=20. (
для x Î [-10; 10]. Шаг рассчитать самостоятельно, количество точек разбиения отрезка n=20. (  , xi = a + i*h или xi+1=xi+h)
, xi = a + i*h или xi+1=xi+h) для x Î [0,1; 5,05] при n=20.
для x Î [0,1; 5,05] при n=20.
 .
. .
. , то есть для эллипса, если коэффициент В=0. эксцентриситет e<1. Схематичное изображение эллипса представлено на рис.5.
, то есть для эллипса, если коэффициент В=0. эксцентриситет e<1. Схематичное изображение эллипса представлено на рис.5.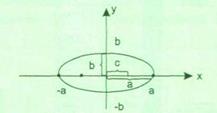
 диапазон и шаг выбрать самостоятельно.
диапазон и шаг выбрать самостоятельно.