
|
|
Угловое ускорение тела, вращающегося вокруг неподвижной осиУгловое ускорение тела характеризует скорость изменения угловой скорости во времени.
Угловое ускорение является скользящим вектором, направленным по оси вращения тела.
Если Если Если Если
Скорость и ускорениет точек, вращающегося вокрук неподвижной оси Скорости точек тела, вращающегося вокруг неподвижной оси
Тогда Линейная скорость точки тела, вращающегося вокруг неподвижной оси, по величине равна произведению радиуса вращения на величину угловой скорости. Теорема Эйлера. Вектор линейной скорости точки тела, вращающегося вокруг неподвижной оси, равен векторному произведению угловой скорости на радиус-вектор точки:
Где Тогда Ускорения точек тела, вращающегося вокруг неподвижной оси Согласно теореме о разложении ускорения имеем:
Тогда
Нормальное ускорение точки тела при вращении его вокруг неподвижной оси равно произведению радиуса вращения на квадрат угловой скорости. Касательное ускорение равно произведению радиуса вращения на угловое ускорение.
Скорость и ускорение точек тела при плоско-паралеьном движении Плоско-параллельным или плоским движением твердого тела называется такое движение, при котором все точки тела движутся в плоскостях, параллельных некоторой неподвижной плоскости.
Теорема. Перемещение плоской фигуры в ее плоскости можно осуществить путем поступательного перемещения вместе с полюсом и вращения вокруг полюса. При этом угол поворота не зависит от выбора полюса. Доказательство
Кинематические уравнения плоско-параллельного движения
Скорость точек тела при плоско-параллельном движении Теорема. При плоско-параллельном движении твердого тела скорость любой ее точки равна векторной сумме скорости полюса и скорости точки во вращательном движении вокруг полюса. Доказательство
Теорема о проекциях скоростей двух точек тела Теорема. Проекции скоростей двух точек твердого тела на ось, проходящую через эти точки, равны друг другу. Доказательство
Ускорения точек при плоско-параллельном движении Теорема. Ускорение любой точки тела при плоско-параллельном движении равно векторной сумме ускорения полюса, вращательного (тангенциального) и центростремительного (нормального) ускорений. Доказательство
Или где тогда
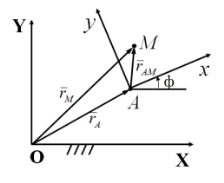
Сложное движение точки. Абсолютная и относительная производные вектора. Сложное движение точки Движение точки M относительно абсолютной системы координат OXYZ называется абсолютным. Движение точки M относительно подвижной системы координат Axyz называется относительным. Движение, совершаемое подвижной системы координат Axyz по отношению к абсолютной системе координат OXYZ, является для точки M переносным движением. Уравнения абсолютного движения точки M:
Уравнения относительного движения точки M:
Абсолютная и относительная производные вектора
Обозначим:
Согласно формуле Эйлера:
Тогда
Следовательно
Теорема о сложении скоростей и ускорении Теорема о сложении скоростей Теорема. Абсолютная скорость точки равна векторной суммевввввввввввв переносной и относительной скоростей.
Где Тогда Следовательно Теорема о сложении ускорений Теорема. Абсолютное ускорение точки равно векторной сумме переносного, относительного и кориолисова ускорений. Доказательство
где
Тогда
Где Следовательно
Окончательно получим
Кориолисово ускорение равно нулю в следующих случаях: 1) при 2) когда 3) когда

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|






 то вращение тела называется ускоренным.
то вращение тела называется ускоренным. то вращение тела называется замедленным.
то вращение тела называется замедленным. то вращение тела называется равномерным.
то вращение тела называется равномерным. то вращение тела называется равнопеременным.
то вращение тела называется равнопеременным. Скорость любой точки тела, вращающегося вокруг неподвижной оси, называется линейной или окружной скоростью.
Скорость любой точки тела, вращающегося вокруг неподвижной оси, называется линейной или окружной скоростью. Пусть за элементарное время dt точка M совершает элементарное перемещение ds=Rdφ
Пусть за элементарное время dt точка M совершает элементарное перемещение ds=Rdφ или
или 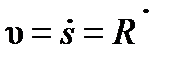
 Доказательство
Доказательство

 Тогда из определения о векторном произведении двух векторов
Тогда из определения о векторном произведении двух векторов  и
и  получаем
получаем 





 где
где 











 или
или  ,
, 




 матрица вращения подвижной системы координат Аxh
матрица вращения подвижной системы координат Аxh
 где
где
 жуйе
жуйе


 где
где  тогда
тогда 
















 - абсолютная производная вектора
- абсолютная производная вектора 
 - относительная производная вектора
- относительная производная вектора 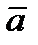






 где
где


 или
или 
 где
где 





 -абс. ускорение точки
-абс. ускорение точки - ускорение точки А
- ускорение точки А - угловое ускорение подв. системы координат Axyz
- угловое ускорение подв. системы координат Axyz где
где  - относительная скорость
- относительная скорость 
 где
где - относительное ускорение
- относительное ускорение

 - переносное ускорение
- переносное ускорение где
где - поворотное (кориолисово) ускорение
- поворотное (кориолисово) ускорение где
где 



 , это будет при поступательном перемещении подвижной системы координат;
, это будет при поступательном перемещении подвижной системы координат; параллельна
параллельна  ;
; .
.