
|
|
Упрощенная и полная формулы Клосса АД
Для расчета МХ по формуле (2.29) нужны сопротивления обмоток АД. Однако указанные сопротивления редко приводятся в каталожных данных АД и никогда не выносятся на шильдик (этикетку), прикрепленный к корпусу двигателя. Такое положение с расчетами МХ АД объясняется тем, что МХ может быть просто рассчитана по значениям в особых точках МХ, а именно: - по номинальным значениям вращающего момента Мном и частоты ωном (фактически задаются номинальная мощность Рном и номинальная частота пном, но которые просто пересчитываются в Мном и ωном по формулам - и по перегрузочной способности λ. Такие формулы расчета МХ называются формулами Клосса. Существуют упрощенная и полная формулы Клосса. Вывод упрощенной формулы Клосса. Для вывода используется выражение МХ в виде (2.29), но в котором принято R1=0. Такое упрощение формулы (2.29) обосновывается следующим: - величины сопротивлений R1 и - диапазон рабочих скольжений АД, работающего без перегрузки, не превышает значения sном=0,02...0,06 (2.30) и поэтому 1/s=17..50>>1; - в сумме Выражение (2.29) МХ АД примет вид
Момент М принимает максимальное (критическое) значение Мк при таком скольжении s, когда знаменатель выражения (2.31) будет минимальным. Условием минимума названного знаменателя является равенство нулю производной от него по скольжению s:
Подставляем sк из (2.32) в формулу (2.31) и рассчитываем Мк:
Представляем выражение (2.31) в виде, допускающем применение к нему подстановки (2.33) и выполняем преобразования:
Последнее выражение ряда (2.34) является упрощенной формулой Клосса. Критическое скольжение sк не является каталожной величиной, но оно может быть найдено из формулы (2.34), если в правую часть ее подставить номинальное скольжение sном, а в левую – номинальный момент Мном:
Упрощенная формула Клосса достаточно точна на участке от критической ωк частоты вращения АД до синхронной частоты ω0 (рис.2.17). Однако на разгонном участке МХ от нулевой частоты ω до критической ωк формула даёт значительную погрешность. Полная формула Клосса. При выводе полной формулы Клосса используется выражение МХ (2.29) без каких-либо упрощений. Полная формула Клосса имеет вид
Вопросы и задания 1. Приведите выражения упрощенной и полной формулы Клосса. 2. Как рассчитать критические скольжение и момент через параметры обмоток АД? 3. Как рассчитать критический момент через каталожные данные АД?
2.10 Устойчивости работы АД "в малом" и "в большом"
Под устойчивостью работы электродвигателя понимают способность двигателя восстанавливать установившуюся частоту вращения при кратковременных возмущениях (изменениях нагрузки, напряжения питающей сети и пр.). При анализе устойчивости используется уравнение механики
где J – момент инерции нагрузки; МС – момент сопротивления нагрузки; М и ω – вращающий момент и частота вращения АД. Из уравнения механики следует: - если M>MC, то - если M<MC, то - если M=MC, то Работу нагруженного АД удобно анализировать графическим методом с использованием механических характеристик АД и нагрузки (рис.2.18). Тогда установившемся режимам соответствуют точки пересечения графиков. Различают устойчивость работы "в малом" и "в большом". Устойчивость работы АД "в малом". Устойчивость работы "в малом" устанавливается для режимов с малыми отклонениями от установившегося режима (рис.2.18,а). Механические характеристики АД и нагрузки пересекаются в точках 1 и 2 и только в них, в соответствии с (2.37), могут быть установившиеся режимы. Однако, существование точек пересечения еще не достаточно для их устойчивости. Необходимо еще учитывать наклоны МХ в точках их пересечения. Исследуем на устойчивость точку 1. Пусть случайно частота вращения АД увеличилась, стала больше ω1 и ей на графиках МХ соответствуют точки 3' и 3". Вращающий момент М АД, определяемый точкой 3', будет меньше момента сопротивления МС нагрузки, определяемого точкой 3", и, поэтому, частота вращения АД будет снижаться до тех пор, пока будет достигнута точка 1. Теперь пусть случайно частота вращения АД уменьшилась, стала меньше ω1 и ей на графиках МХ соответствуют точки 4' и 4". Вращающий момент М АД, определяемый точкой 4', будет больше момента сопротивления МС нагрузки, определяемого точкой 4", и, поэтому, частота вращения АД будет увеличиваться до тех пор, пока будет достигнута точка 1. Таким образом точка 1 является устойчивой точкой установившегося режима работы АД. Исследуем теперь на устойчивость точку 2. Пусть случайно частота вращения АД увеличилась, стала больше ω2 и ей на графиках МХ соответствуют точки 5' и 5". Вращающий момент М АД, определяемый точкой 5', будет больше момента сопротивления МС нагрузки, определяемого точкой 5", и, поэтому, частота вращения АД будет повышаться до тех пор, пока будет достигнута точка 1. Теперь пусть случайно частота вращения АД уменьшилась, стала меньше ω2 и ей на графиках МХ соответствуют точки 6' и 6". Вращающий момент М АД, определяемый точкой 6', будет меньше момента сопротивления МС нагрузки, определяемого точкой 4", и, поэтому, частота вращения АД будет уменьшаться до тех пор, пока двигатель остановится. Таким образом точка 2 является неустойчивой точкой установившегося режима работы АД.
Условие устойчивости в точке 1 может быть записано в аналитической форме в виде неравенства, полученного из линеаризованного уравнения (2.37) для малых отклонений частоты Δω:
Линеаризованное уравнение механики оказалось операторным уравнением первого порядка. По критерию устойчивости Гурвица система первого порядка будет устойчива, если положительны оба коэффициента операторного уравнения, т.е.
В точке 1 неравенство (2.39) выполняется, а в точке 2 – нет. Устойчивым рабочим участком МХ АД является участок с частотой вращения, превышающей критическую частоту ωк, а на частотах ниже критической ωк работа АД неустойчива. Неустойчивый участок называется разгонным участком АД. Условием разгона двигателя является превышение моментом АД момента сопротивления нагрузки на протяжении всего разгонного участка. Устойчивость работы АД "в большом". Устойчивость работы "в большом" устанавливается для режимов с большими отклонениями от установившегося режима (рис.2.18,б). К большим изменениям относятся: - глубокое понижение напряжения питания АД, переводящие естественную МХ M=f1(ω) в такую искусственную M=f2(ω), которая с МХ нагрузки MС=f(ω) не пересекается, что приведет к остановке АД; - большое увеличение момента сопротивления нагрузки, так что график МХ нагрузки, показанный пунктиром, не будет пересекать МХ АД и двигатель остановится. Вопросы и задания 1. Как с помощью уравнения механики вращательного движения можно судить об устойчивости работы нагруженного АД? 2. Как доказать устойчивость работы "в малом" на рабочем участке МХ АД? 3. Как доказать неустойчивость работы "в малом" на разгонном участке МХ АД? 4. Что такое устойчивость работы АД "в большом"?

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 );
);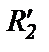 практически одинаковые;
практически одинаковые;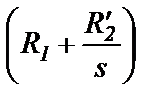 первое слагаемое R1 намного меньше второго
первое слагаемое R1 намного меньше второго  , поэтому сопротивлением R1 можно пренебречь.
, поэтому сопротивлением R1 можно пренебречь. (2.31)
(2.31) (2.32)
(2.32) (2.33)
(2.33) (2.34)
(2.34)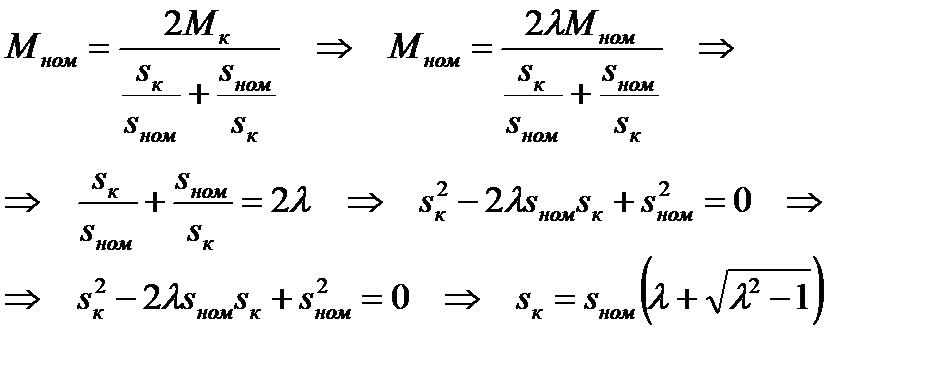 (2.35)
(2.35)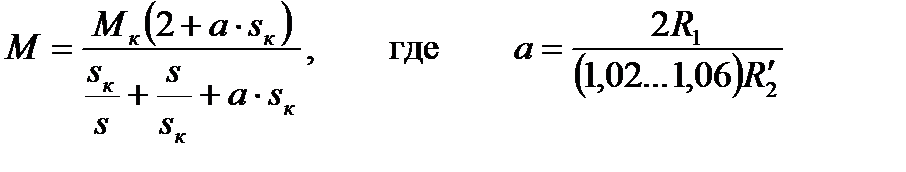 (2.36)
(2.36)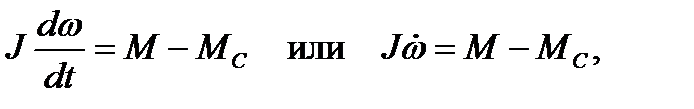 (2.37)
(2.37)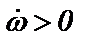 и частота вращения двигателя увеличивается;
и частота вращения двигателя увеличивается; и частота вращения двигателя уменьшается;
и частота вращения двигателя уменьшается; и двигатель работает в установившемся режиме.
и двигатель работает в установившемся режиме.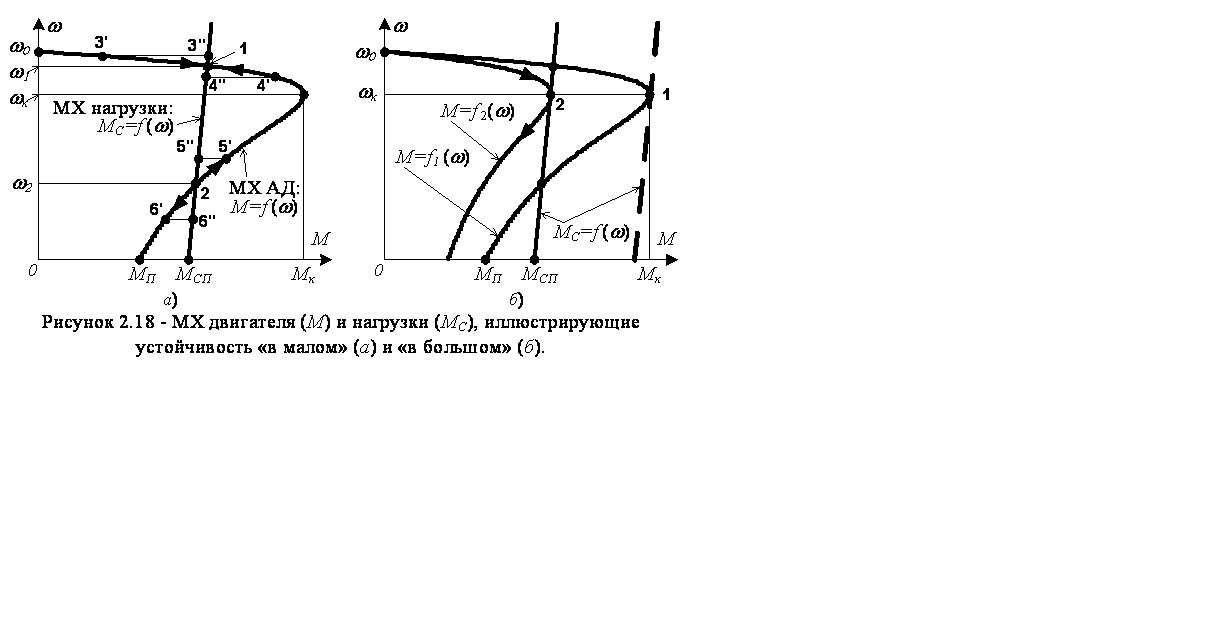
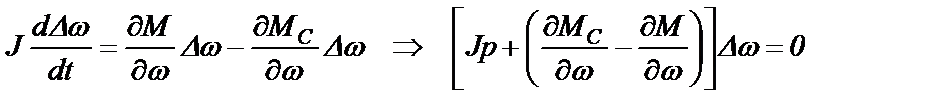 (2.38)
(2.38) (2.39)
(2.39)