
|
|
Устройство и принцип действия однофазного трансформатора. Коэффициент трансформации напряженийСУДОВЫЕ ЭЛЕКТРИЧЕСКИЕ МАШИНЫ
Конспект лекций
Том 1
для студентов специальности 5.07010407 “Эксплуатация электрооборудования и автоматики судов” дневной формы обучения
Керчь, 2014 СОДЕРЖАНИЕ
Введение . . . . . . . . . . . . 3 1 Трансформаторы. . . . . . . . . . . 4 1.1 Устройство и принцип действия однофазного трансформатора Коэффициент трансформации напряжений . . . . . . . 4 1.2 Работа однофазного трансформатора под нагрузкой. Трансформация токов . . 5 1.3 Индуктивное сопротивление рассеяния. Приведенный однофазный трансформатор. Пересчет параметров вторичной обмотки . . . . . . . 6 1.4 Опыты холостого хода и короткого замыкания однофазного трансформатора . . 8 1.5 Уравнения однофазного трансформатора. Векторная диаграмма нагруженного трансформатора . . . . . . . . . . . 10 1.6 Внешняя характеристика однофазного трансформатора. Расчет потерь напряжения . 11 1.7 Энергетическая диаграмма и КПД однофазного трансформатора . . . . 13 1.8 Устройство трехфазного трансформатора и группы соединения его обмоток . . 14 1.9 Уравнения трехфазного трансформатора. Векторные диаграммы нагруженного трансформатора . . . . . . . . . 16 1.10 Параллельная работа трехфазных трансформаторов . . . . . 18 1.11 Автотрансформатор, устройство, принцип действия, основные характеристики . 24 1.12 Сварочные трансформаторы, устройство, принцип действия, основные характеристики 26 1.13 Измерительные трансформаторы напряжения и тока . . . . . 27 2 Асинхронные двигатели . . . . . . . . . . 29 2.1 Устройство и принцип действия трехфазного асинхронного двигателя . . . 29 2.2 Условия получения вращающегося магнитного поля статора . . . . 31 2.3 Однослойные обмотки статора АД: простая и распределенная . . . . 33 2.4 Двухслойные петлевые обмотки статора АД с укороченным шагом . . 35 2.5 Работа заторможенного АД при разомкнутом изамкнутом роторе. Индукционный регулятор напряжения . . . . . . . . 40 2.6 Работа вращающегося АД. Параметры э.д.с.и тока ротора. Энергетическая диаграмма и вращающий момент АД . . . . . 41 2.7 Приведение ротора к статору. Схемы замещения АД . . . . . 43 2.8 Механическая и электромеханическая характеристики АД . . . . 45 2.9 Упрощенная и полная формулы Клосса АД . . . . . . 47 2.10 Устойчивости работы АД "в малом" и "в большом" . . . . . 49 2.11 Устройство и принцип действия АД с двухклеточным и глубокопазным ротором . . . . . . . . . . 51 2.12 Механические характеристики АД с двухклеточным и глубокопазным ротором . . . . . . . . . . 54 2.13 Определение параметров двухклеточного ротора по каталожным данным АД . 56 2.14 Способы пуска АД . . . . . . . . . . 59 2.15 Частотное регулирование скорости АД по цепи статора . . . . . 62 2.16 Регулирование частоты вращения АД с фазным ротором . . . . 65 2.17 Полюсопереключаемые АД . . . . . . . . . 67 2.18 Способы торможения АД . . . . . . . . . 70 2.19 Однофазный однообмоточный АД . . . . . . . . 73 2.20 Однофазный двухобмоточный АД . . . . . . . . 75
ВВЕДЕНИЕ Электрическими называют машины, совершающие преобразование механической энергии в электрическую, передачу ее на расстояние и обратное преобразование электрической энергии в механическую. Электрическая машина (ЭМ), предназначенная для преобразования механической энергии в электрическую, называется генератором. ЭМ, предназначенная для обратного преобразования энергии, называется двигателем. ЭМ, предназначенная для преобразования параметров электрической энергии с целью передачи ее на расстояние, называется трансформатором. ЭМ представляет собой электромагнитную систему, состоящую из взаимосвязанных магнитных и электрических цепей. Магнитная цепь включает неподвижный и подвижный магнитопроводы и немагнитный воздушный зазор, отделяющий их друг от друга. Электрические цепи образуются обмотками, которые могут перемещаться друг относительно друга совместно с магнитопроводами, на которых они размещены. Электромеханическое преобразование энергии в ЭМ основано на явлениях получения электродвижущей силы, электрического тока, магнитного поля и механической силы. ЭМ могут быть рассчитаны для работы с сетью переменного и постоянного тока. В соответствии с этим они делятся на ЭМ переменного тока и ЭМ постоянного тока. Цель курса ЭМ – дать студентам основы теории, конструкции, характеристик и особенностей работы электрических машин. В результате изучения дисциплины студенты должны знать: - конструкцию электрических машин и их принцип действия; - рабочие характеристики электрических машин; - варианты использования электрических машин по назначению. Студенты должны уметь: - использовать электрические машины по их прямому назначению; - оценивать (диагностировать) техническое состояние электрических машин; - организовывать техническое обслуживание судовых электрических машин. ТРАНСФОРМАТОРЫ Устройство и принцип действия однофазного трансформатора. Коэффициент трансформации напряжений
Однофазный трансформатор содержит катушки с намотанными на них обмотками, которые посажены на замкнутый сердечник (магнитопровод) из электротехнической стали. Катушки называются первичной и вторичной обмотками, которые имеют, соответственно, w1 и w2 число витков (рис.1.1). Первичная обмотка одна-единственная, а вторичных обмоток может быть больше одной. Первичная обмотка подключается к источнику переменного напряжения (в сеть) U1. С вторичной обмотки снимается переменное напряжение U2. Трансформатор может работать как в режиме холостого хода (х.х.), когда вторичная обмотка разомкнута (рис.1.1,а), так и под нагрузкой, когда к вторичной обмотке подключено сопротивление нагрузки (нагрузка) zн (рис.1.1,б).
Работа трансформатора на холостом ходу (рис.1.1,а). Первичная обмотка w1 подключена к сети с напряжением U1 и так как из сети и обмотки образована замкнутая цепь, то по обмотке потечет переменный ток I1. Переменный ток I1 создаст в катушке переменное магнитное поле Ф1, которое практически полностью будет сосредоточено в магнитопроводе. На магнитопроводе помещена вторичная обмотка w2 и переменное магнитное поле Ф1 пересекает контуры (витки) вторичной обмотки и, поэтому в ней наведется электродвижущая сила (э.д.с.) Е2. Концы вторичной обмотки выведены наружу трансформатора и на этих выводах будет присутствовать напряжение U2, которое в точности будет равно э.д.с. Е2 (так как вторичная обмотка разомкнута). Таким образом, в трансформаторе произошло преобразование переменных напряжений: U1 преобразовалось в напряжение U2. Одновременно переменное магнитное поле Ф1 пересекает контуры (витки) первичной обмотки и, поэтому в ней наведется электродвижущая сила (э.д.с.) Е1. Так как общий (суммарный) магнитный поток ФΣ одинаков для витков обоих обмоток и, поэтому, в каждом витке обмоток индуктируется одинаковая по величине э.д.с., которую обозначим как Евит. Э.д.с. обмоток будут прямо пропорциональны числам их витков w1 и w2:
Из (1.1) следует, что отношение э.д.с. обмоток равно отношению их числа витков:
Коэффициент трансформации. Коэффициентом трансформации kтр называют следующее отношение напряжений U1 и U2 на обмотках:
Ввиду реальной (подтвержденной опытным путем) малости падения напряжения на внутреннем сопротивлении z1 первичной обмотки, э.д.с. Е1 будет практически равной напряжению U1: Формула коэффициента трансформации с учетом (1.3) и (1.2) примет вид:
Из последней формулы следует, что коэффициент трансформации kтр можно рассчитывать как конструктивную характеристику трансформатора (без подключения трансформатора к сети). Это удобно. Если U2>U1, то трансформатор называют повышающим и его kтр<1. Если U2<U1, то трансформатор называют понижающим и его kтр>1. Вопросы и задания 1. Поясните устройство трансформатора, назначение катушек и магнитопровода. 2. Объясните принцип действия трансформатора. 3. Почему в первичной обмотке, подключенной к сети, возникает э.д.с Е1? В каком соотношении находится э.д.с Е1 с напряжением сети U1? 4. Что такое коэффициент трансформации kтр и какие варианты расчета его существуют?
1.2 Работа однофазного трансформатора под нагрузкой. Трансформация токов
К выводам вторичной обмотки подключается нагрузка zн (рис.1.1,б). В подключенной к сети первичной обмотке протекает переменный ток I1, который создаст в магнитопроводе переменный магнитный поток Ф1. Переменный магнитный поток Ф1 будет пересекать витки вторичной обмотки и, поэтому, в ней наведется переменная э.д.с. Е2. Так как вторичная обмотка вместе с сопротивлением zн образуют замкнутый контур, то в контуре и в самой вторичной обмотке потечет переменный ток I2. Переменны ток I2 создаст вв вторичной катушке и в магниторпроводе переменное магнитное поле Ф2. Если напряжение U1 синусоидально, то синусоидален созданный им ток I1, синусоидально поле Ф1, синусоидальны э.д.с. Е2 и ток I2 и, наконец, синусоидально поле Ф2. Определенное по правилу Ленца магнитное поле Ф2 будет находиться в противофазе с полем Ф1. Этот факт на рис.1.1,б отражен тем, что потоки Ф1 и Ф2 направлены в магнитопроводе встречно. Два встречных магнитных потока создадут одно суммарное поле:
Суммарное поле ФΣ наводит в обоих обмотках э.д.с. Е1 и Е2. При реальных малых внутренних сопротивлениях z1 и z2 обмоток трансформатора различия между э.д.с. Е1 и Е2 и соответствующими напряжениями U1 и U2 незначительны (2..3%) независимо от степени загрузки трансформатора. Поэтому, при постоянном действующем значении сетевого напряжения U1 действующее значение э.д.с. Е1 также будет постоянным. Если э.д.с. Е1 создается переменным магнитным полем ФΣ, то при постоянстве действующего значения э.д.с. Е1, также будет постоянна амплитуда магнитного потока ФΣ. Это явление, наблюдающееся в трансформаторе, называется принципом постоянства магнитного поля в сердечнике трансформатора. Так как ФΣ связан с потоками Ф1 и Ф2 соотношением (1.5), то при возрастании тока I2 вторичной обмотки и создаваемого им магнитного потока Ф2 должен увеличиться магнитный поток Ф1. Это возможно только одним путем – увеличением потребляемого из сети тока I1. Значит, I1 отслеживает изменения тока I2: если I2 изменится, вслед за ним пропорционально изменится ток I1. Описанное явление называется трансформацией токов в трансформаторе. Числовой характеристикой взаимозависимости токов является коэффициент трансформации токов:
Числовое значения коэффициента трансформации токов для нагруженного трансформатора практически совпадает с базовым определением коэффициента трансформации через напряжения обмоток (1.3):
Из последнего равенства цепи (1.7) следует вывод: полные мощности первичной и вторичной обмоток практически одинаковы. Это значит, что в трансформаторе не происходит преобразования мощности, а преобразуются только напряжения и токи. Вопросы и задания 1. Как создается суммарный магнитный поток ФΣ? 2. Объясните принцип постоянства суммарного магнитного потока ФΣ. 3. Что такое коэффициент трансформации токов? 4. Объясните принцип постоянства полной мощности трансформатора. 1.3 Индуктивное сопротивление рассеяния. Приведенный однофазный трансформатор. Пересчет параметров вторичной обмотки Определение индуктивного сопротивления рассеяния.
Ток I в обмотке трансформатора создает магнитное поле Ф, направление которого определяется правилом буравчика. Поле представляет собой замкнутые линии, которые окружают проводник витка с током и которые вложены друг в друга. Между обмоткой и сердечником существует технологический зазор δ, образованный толщиной стенок каркаса катушки, многослойно намоткой обмотки с применением изоляционных прокладок между слоями. Те лини магнитного поля, которые не достигли тела магнитопровода, образуют поля рассеяния Фр. Более удаленные линии магнитного поля проникают в магнитопровод и создают в нем основное магнитное поле Фосн. Благодаря полю Фосн осуществляется трансформация напряжений между посаженными на сердечник обмотками, что определяет использование трансформатора по назначению. Поля Фр, находящиеся вне сердечника, в трансформации напряжений не участвуют и, поэтому их называют полями рассеяния. Поля Фр, как созданные током I в катушке, прямо пропорциональны току: Фр ~ I. (1.8) В то же время поля Фр являются переменными, так как ток I в катушке переменный. Переменное магнитное поле Фр индуктирует в катушке э.д.с. рассеяния Ер, которая прямо пропорциональна ему: Ер ~ Фр (1.9) Из пропорций (1.8) и (1.9) следует, что между э.д.с. Ер и током Фр ~ I также существует прямая пропорция: Ер ~ I (1.10) Известно, что законом Ома устанавливается пропорция между напряжением цепи и током в ней и коэффициентом пропорциональности является сопротивление. Применим формально к выражению (1.10) закон Ома:
где хр называют индуктивным сопротивлением рассеяния. Теперь используем следующие факты относительно переменных Ер, Фр и I. Ток I и магнитный поток Фр синфазны, а э.д.с. Ер отстает по фазе от потока Фр на угол 90○. Следовательно, э.д.с. Ер отстает от тока I на угол 90○. В комплексных переменных отстающему на угол 90○ сигналу соответствует символ -j. С учетом указанного фазового сдвига между Ер и I выражение (1.11) может быть заменено на векторное:
Приведенный однофазный трансформатор. Процедура приведения трансформатора заключается его в замене электрической схемы, содержащей две индуктивно связанные катушки, на схему с непосредственным соединением первичной и вторичной обмоток. Расчет последней схемы будет проще, так как в ней не будет индуктивной связи. Процедура приведения поясняется серией рисунков (рис.1.3).
На рис.1.3,а приведена исходная схема физического трансформатора. Затем каждая из обмоток представляется (рис.1.3,б) в виде источника э.д.с. Е1 и Е2, индуктивного сопротивления рассеяния хр1 и хр2 и активных сопротивлений R1 и R2 проводников обмоток. В последней схеме Е1 и Е2 не равны друг другу, так у обмоток неодинаковые числа витков w1 и w2. Изменяем число витков w2 вторичной обмотки так, чтобы оно стало равным числу витков w1 первичной обмотки (рис.1.3,в). В результате э.д.с. Е2 станет равной э.д.с. Е1. Изменившуюся э.д.с. Е2 обозначим как При работе трансформатора под нагрузкой близкой к номинальной ток I0 намного меньше двух других токов I1 и Пересчет параметров вторичной обмотки. У приведенной вторичной обмотки для ее параметры и сигналов применены обозначения
При выводе формул использовались равенство активных, реактивных и полных мощностей на всех одноименных элементах исходной схемы трансформатора и его схемы замещения. Расчеты, например, напряжения U2 и тока I2 в нагрузке с использованием полной схемы замещения трансформатора выполнятся по следующему алгоритму: 1. По формулам с 3-й по 7-ю системы (1.13) переводятся все физические сопротивления в приведенные. Сопротивления первичной обмотки xр1 и R1 и цепи намагничивания x0 и R0 берутся не пересчитанными. 2. По схеме замещения (рис.1.3,д) методами теории цепей рассчитываются все токи и напряжения, в том числе и 3. По формулам, обратным к формулам 1 и 2 системы (1.13), рассчитывают физические напряжение U2 и ток I2. Вопросы и задания 1. Поясните картину магнитного поля катушки трансформатора и смысл названий потоков основного и рассеяния. 2. Как выводится индуктивное сопротивление рассеяния? 3. Поясните этапы приведения трансформатора. 4. Какие существуют схемы замещения трансформатора? 5. Какой алгоритм расчета по схеме замещения трансформатора? 1.4 Опыты холостого хода и короткого замыкания однофазного трансформатора
Сопротивления схемы замещения трансформатора принято определять экспериментально из опытов холостого хода и короткого замыкания. Опыт холостого хода. Схема опыта приведена на рис.1.4,а. Условия проведения опыта: - вторичная обмотка w2 разомкнута; - на первичную обмотку w1 подается номинальное напряжение U1ном.
Подключенными приборами измеряются: напряжения U1 и U2 первичной и вторичной обмоток, ток холостого хода I1=Ixx первичной обмотки и потребляемая активная мощность Р1. Так как ток во вторичной обмотке нулевой, а ток первичной обмотки Ixx мал, то потерями мощности в активных сопротивлениях обмоток можно пренебречь. Магнитный поток в сердечнике номинальный, так как к трансформатору приложено номинальное напряжение U1ном. Измеренная активная мощность Р1 является номинальной мощностью потерь в стали Р1=Рст.ном. Схема замещения для опыта представлена на рис.1.4,б. Так как в разомкнутой вторичной обмотке ток нулевой, то нулевым будет падение напряжения DU2=0 на внутреннем сопротивлении обмотки. Вследствие этого внутреннее сопротивление вторичной обмотки можно считать нулевым. У реальных трансформаторов внутренние сопротивления хр1 и R1 первичной обмотки намного меньше сопротивлений х0 и R0 цепи намагничивания: R1<<R0 и xp1<<x0. Поэтому внутренними сопротивлениями первичной обмотки можно пренебречь и считать их нулевыми. На схеме замещения внутренние сопротивления обоих обмоток показаны закороченными. По измеренным значениям рассчитывают: 1) сопротивления R0 и x0 цепи намагничивания по формулам
2) коэффициент трансформации
Опыт короткого замыкания. Схема опыта приведена на рис.1.5,а. Условия проведения опыта: - вторичная обмотка w2 замкнута на амперметр с практически нулевым внутренним сопротивлением; - на первичную обмотку w1 подается пониженное напряжение Uкз такой величины, при котором во вторичной обмотке протекает номинальный ток I2ном.
Подключенными приборами измеряются: напряжение U1 первичной обмотки, токи I1 и I2 первичной и вторичной обмоток и потребляемая активная мощность Р1. Напряжение короткого замыкания Uкз мало и составляет всего 4...7% от номинального. Магнитный поток в магнитопроводе, который пропорционален Uкз, также очень мал и потери мощности в стали Рст, которые пропорциональны При проведении опыта контролируется на равенство номинальному тока I2 вторичной обмотки. В силу свойства трансформатора трансформировать ток, номинальным будет также ток и первичной обмотки I1ном. Значит измеренные потери мощности являются номинальными потерями в меди Рм.ном обмоток. В полной схеме замещения для опыта, представленной на рис.1.5,в, цепью намагничивания можно пренебречь, так как ток I0 в ней намного меньше токов I1 и I'2. Объединив, затем, активные R1, R'2 и реактивные сопротивления рассеяния xp1, x'p2 обмоток в сопротивления, соответственно, Rк и хк, получим простейшую схему замещения (рис.1.5,в) для опыта короткого замыкания. По измеренным значениям рассчитывают: 1) сопротивления Rк и xк короткого замыкания по формулам
2) активные R1, R'2 и реактивные сопротивления рассеяния xp1, x'p2 обмоток, принимаемые равными половине сопротивлений Rк и хк короткого замыкания:
и физические сопротивления вторичной обмотки (см. формулы (1.13)):
Вопросы и задания 1. Назовите условия проведения опыта холостого хода и определяемые по результатам опыта параметры схемы замещения трансформатора. 2. Поясните вид схемы замещения трансформатора и смысл измеренных сигналов в опыте холостого хода. 3. Назовите условия проведения опыта короткого замыкания и определяемые по результатам опыта параметры схемы замещения трансформатора. 4. Поясните вид схемы замещения трансформатора и смысл измеренных сигналов в опыте короткого замыкания.
1.5 Уравнения однофазного трансформатора. Векторная диаграмма нагруженного трансформатора Система уравнений однофазного трансформатора состоит из уравнений, которыми описывается полная схема замещения его (рис.1.3,д), и уравнение нагрузки:
Для нагруженного трансформатора заданными величинами являются: - напряжение сети U1; - сопротивления R1, R'2, xp1, x'p2, R0, x0 схемы замещения трансформатора; - сопротивления Rн, xн нагрузки. Этих данных достаточно для того, чтобы рассчитать напряжение U2 на нагрузке по уравнениям системы (1.18). Расчет можно выполнить как аналитически символическим методом, так и графо-аналитически с использование векторной диаграммы трансформатора. Порядок построения векторной диаграммы нагруженного трансформатора: 1). Задаемся произвольным числовым значением напряжения
Из 5-го уравнения системы (1.18) рассчитываем по закону Ома ток
Поводим вектор
2). Вычисляем вектора напряжений 3). Из 3-го уравнения системы (1.18) находим параметры тока I0:
Поводим вектор 4). В соответствии с 4-м уравнением системы (1.18) находим вектор тока 5). Вычисляем вектора напряжений 6). При определенной построением длине вектора
и истинное (в п.1 принималось произвольное значение) напряжения U2:
Вопросы и задания 1. Составьте уравнения, описывающие нагруженный трансформатор. 2. Поясните вычисления и построения, позволяющие найти вектор 3. Поясните вычисления и построения, позволяющие найти вектор 1.6 Внешняя характеристика однофазного трансформатора. Расчет потерь напряжения
Внешней характеристикой трансформатора называется зависимость напряжения U2 на нагрузке от протекающего в ней тока I2 при неизменном напряжении сети U1 или, если использовать в расчетах схему замещения трансформатора, - напряжения Трудоемкость вычислений и вид внешней характеристики существенно зависит от вида используемой в расчетах схемы замещения трансформатора. Расчеты по полной схеме замещения можно выполнить с использованием векторной диаграммы, приведенной на рис.1.6. Однако формулы внешней характеристики будут громоздкими и сложными. При расчетах внешней характеристики для нагруженного трансформатора можно использовать простейшую схему замещения, изображенную на рис.1.3,ж. Формулы внешней характеристики будут простейшими с допустимой в инженерных расчетах погрешностью ±5%. Следовательно, допустимо рассматривать только вариант расчета с простейшей схемой замещения трансформатора. Перед выводом формулы внешней характеристики учтем две особенности: 1) в упрощенной схеме отсутствует цепь намагничивания и, поэтому, ток I0 равен нулю, а токи I1 и 2) для реальных трансформаторов угол δ между векторами напряжений С учетом отмеченных особенностей векторная диаграмма трансформатора, из которой выводятся формулы внешней характеристики, будет вида, приведенного на рис.1.7. Так как на рис.1.7 вектора напряжений
Из векторной диаграммы следует
Падение напряжения ΔU'mp на внутреннем сопротивлении Rк+jxк трансформатора равно длине отрезка
После подстановки (1.20) в (1.19) получаем внешнюю характеристику:
График внешней характеристики представляет собой прямую линию (рис.1.8). Наклон внешней характеристики зависит как от внутреннего сопротивления Rк+jxк трансформатора, так и от фазового сдвига φн между током и напряжением нагрузки. Для установления такой зависимости преобразуем выражение (1.21):
где φк - фазовый сдвиг между током и напряжением на внутреннем сопротивлении трансформатора и он для трансформатора является фиксированной величиной, причем 0<φк<90○; β – коэффициент загрузки трансформатора по току. Как следует из (1.22), наклон внешней характеристики зависит от напряжения короткого замыкания Uкз трансформатора и разности (φк-φн) фазовых сдвигов: - чем больше Uкз, тем круче наклон; - для активно-индуктивной нагрузки с 0<φн<90○ наклон всегда отрицательный, так как |(φк-φн)|<90○ и, поэтому cos(φк-φн)>0; - для активно-индуктивной нагрузки отрицательный наклон максимален при (φк-φн)=0; - для активно-емкостной нагрузки с -90○<φн<0 наклон будет нулевым при (φк-φн)=90○ и положительным при (φк-φн)>90○. Вопросы и задания 1. Что такое "внешняя характеристика трансформатора" и чем определяется выбор метода ее расчета? 2. Приведите вывод формулы внешней характеристики трансформатора. 3. От чего зависит наклон внешней характеристики трансформатора? 1.7 Энергетическая диаграмма и КПД однофазного трансформатора Назначением трансформатора является обеспечение нагрузки, подключенной к вторичной обмотке, активной мощностью Р2 при заданном напряжении U2 на ней. При работе трансформатора возникают в нем потери активной мощности в меди Рм, нагревающие обмотки, и потери в стали Рст, разогревающие магнитопровод. Из сети потребляется мощность Р1. Из первичной обмотки во вторичную передается через переменное магнитное поле электромагнитная мощность Рэм. Энергетическая диаграмма отображает в графической форме связь между названными мощностями (рис.1.9). Потери в стали Рст не зависят от приведенного тока нагрузки 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

 (1.1)
(1.1) (1.2)
(1.2) (1.3)
(1.3) . Для вторичной обмотки, тока в которой нет, напряжение U2 будет точно равным э.д.с. Е2: U2=Е2.
. Для вторичной обмотки, тока в которой нет, напряжение U2 будет точно равным э.д.с. Е2: U2=Е2. (1.4)
(1.4) (1.5)
(1.5) (1.6)
(1.6)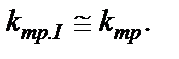 Приравняв два (1.3) и (1.6) определения коэффициента трансформации (через токи и напряжения обмоток), получим:
Приравняв два (1.3) и (1.6) определения коэффициента трансформации (через токи и напряжения обмоток), получим: (1.7)
(1.7) На рис.1.2 приведен чертеж картины магнитных полей обмотки трансформатора.
На рис.1.2 приведен чертеж картины магнитных полей обмотки трансформатора. (1.11)
(1.11) (1.12)
(1.12)
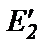 . Также обозначения сопротивлений хр2 и R2 изменим на
. Также обозначения сопротивлений хр2 и R2 изменим на  Так как стало
Так как стало 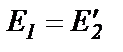 , то между обмотками w1 и
, то между обмотками w1 и  можно установить перемычки (рис.1.3,г), в которых не будет тока, а просто будет механическое объединение физической первичной и приведенной вторичной обмоток. При таком соединении можно считать указанные обмотки считать одной обмоткой, намотанной запараллеленным проводом, и считать ее как одной катушкой с сердечником. Такая катушка представляется в виде последовательно соединенных сопротивлений х0 и R0 с тем их физическим смыслом, что сопротивлением х0 учитывается наличие в катушке основного магнитного поля Фосн, а сопротивлением R0 учитываются потери мощности в стали магнитопровода на гистерезис и вихревые токи. Схема приведенного трансформатора примет окончательный вид (рис.1.3,д). Схема называется полной схемой замещения трансформатора. Между обмотками приведенного трансформатора больше нет магнитной связи.
можно установить перемычки (рис.1.3,г), в которых не будет тока, а просто будет механическое объединение физической первичной и приведенной вторичной обмоток. При таком соединении можно считать указанные обмотки считать одной обмоткой, намотанной запараллеленным проводом, и считать ее как одной катушкой с сердечником. Такая катушка представляется в виде последовательно соединенных сопротивлений х0 и R0 с тем их физическим смыслом, что сопротивлением х0 учитывается наличие в катушке основного магнитного поля Фосн, а сопротивлением R0 учитываются потери мощности в стали магнитопровода на гистерезис и вихревые токи. Схема приведенного трансформатора примет окончательный вид (рис.1.3,д). Схема называется полной схемой замещения трансформатора. Между обмотками приведенного трансформатора больше нет магнитной связи. , и, поэтому, можно цепью намагничивания х0 и R0 можно пренебречь. В результате получаем упрощенную схему замещения трансформатора (рис.1.3,е). Объединением сопротивлений хр1 с
, и, поэтому, можно цепью намагничивания х0 и R0 можно пренебречь. В результате получаем упрощенную схему замещения трансформатора (рис.1.3,е). Объединением сопротивлений хр1 с  и R2 с
и R2 с  получим простейшую схему замещения (рис.1.3,ж), в которой
получим простейшую схему замещения (рис.1.3,ж), в которой  и
и  называют, соответственно, индуктивным и активным сопротивлениями короткого замыкания трансформатора.
называют, соответственно, индуктивным и активным сопротивлениями короткого замыкания трансформатора. . Сопротивления нагрузки тоже должны быть обозначены как приведенные:
. Сопротивления нагрузки тоже должны быть обозначены как приведенные:  У исходного трансформатора перечисленные величины являются физическими и имеют обозначения U2, I2, xp2, R2. zн, xн и Rн. Для того, чтобы можно было в расчетах электрических схем с трансформатором использовать его схему замещения, необходим пересчет физических величин (без штриха) в приведенные (со штрихом). Формулы пересчета имеют вид:
У исходного трансформатора перечисленные величины являются физическими и имеют обозначения U2, I2, xp2, R2. zн, xн и Rн. Для того, чтобы можно было в расчетах электрических схем с трансформатором использовать его схему замещения, необходим пересчет физических величин (без штриха) в приведенные (со штрихом). Формулы пересчета имеют вид: (1.13)
(1.13) .
.
 (1.14)
(1.14)

 и составляют
и составляют  %, что является очень малой величиной. Поэтому потерями мощности в стали можно пренебречь.
%, что является очень малой величиной. Поэтому потерями мощности в стали можно пренебречь. (1.15)
(1.15) (1.16)
(1.16) (1.17)
(1.17) (1.18)
(1.18) . Проводим горизонтально вектор напряжения
. Проводим горизонтально вектор напряжения  , длина которого определяется через величины
, длина которого определяется через величины 
 :
: .
. под углом
под углом  к вектору
к вектору  и
и  , и проводим суммирование в соответствии с 5-м уравнением системы (1.18) векторов
, и проводим суммирование в соответствии с 5-м уравнением системы (1.18) векторов  и
и  . Вектор найденной суммы должен совпасть с вектором
. Вектор найденной суммы должен совпасть с вектором 
 и
и  , и проводим их суммирование в соответствии с 2-м уравнением системы (1.18). Вектор найденной суммы будет вектором
, и проводим их суммирование в соответствии с 2-м уравнением системы (1.18). Вектор найденной суммы будет вектором  .
.
 под углом
под углом  к вектору
к вектору  .
.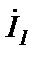 как сумму векторов
как сумму векторов  и
и  .
. и
и  , и проводим их суммирование с вектором
, и проводим их суммирование с вектором  напряжения сети.
напряжения сети.
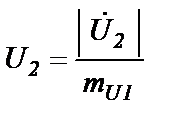
 от тока
от тока 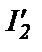 при неизменном U1.
при неизменном U1. совпадают и, следовательно, в расчетах можно использовать только ток
совпадают и, следовательно, в расчетах можно использовать только ток  и
и 
 . (1.19)
. (1.19) , который является суммой отрезков
, который является суммой отрезков  и
и  . Из диаграммы, как чертежа, следует формула потерь напряжения в нагруженном трансформаторе
. Из диаграммы, как чертежа, следует формула потерь напряжения в нагруженном трансформаторе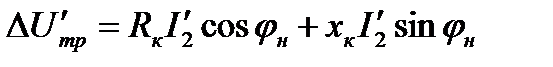 (1.20)
(1.20) (1.21)
(1.21) (1.22)
(1.22) и от физического тока I2 и, следовательно, от коэффициента загрузки трансформатора β.
и от физического тока I2 и, следовательно, от коэффициента загрузки трансформатора β.