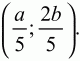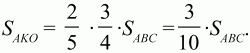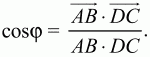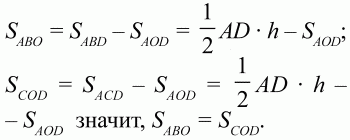Задачи, решаемые координатным и векторным методами

Вообще говоря, в данном случае речь идет не о частных идеях решения определенного класса задач, а об универсальных методах решения самых разнообразных геометрических проблем.

Суть метода состоит в том, что для решения задач вводится система координат (прямоугольная или аффинная), пишутся необходимые уравнения прямых, других фигур, по известным формулам находятся длины и углы.

Примеры решения задач

149. Даны точки А(-2; 1); В(1; 5); С(3; -2); D(6; 2). Является ли четырёхугольник ABCD параллелограммом? Ответ: обоснуйте. (1)

Решение. АВ = (3; 4); CD = (3; 4). Противоположные стороны четырёхугольника, таким образом, равны и параллельны. Значит, ABCD – параллелограмм.

Ответ: ABCD – параллелограмм.

150. В треугольнике ABC точка М – точка пересечения медиан. Выразите вектор AM через вектора АВ и АС (рис. 205). (2)

Рис. 205.

Решение. Медианы точкой пересечения делятся в отношении 2:1, считая от вершины, поэтому

Задачу можно решить проще, если достроить треугольник ABC до параллелограмма ABDC, тогда AM = 2/3 АК, но АК = 1/2 AD = 1/2 (АВ + АС). Отсюда сразу получаем, что AM = 1/3(АВ + АС).

Ответ: 1/3(АВ + АС).

151. В прямоугольнике ABCD точки М и N – середины сторон АВ и ВС. Точка О – точка пересечения AN и DM. Найдите AO/ON (рис. 206). (2)

Рис. 206.

Решение. Решим задачу аналитическим путём. Пусть А(0; 0); D (a; 0); B(0; b), тогда M(0; b/2); N(a/2; b). Напишем уравнения прямых AN и MD.

Точка О будет иметь координаты:

Ответ: 2:3.

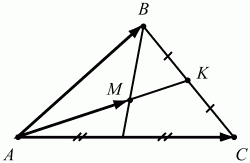
152. ВМ: МС = 3:1, АК = КВ. Найдите: SAKO/SABC (рис. 207). (3)

Рис. 207.

Решение. См. задачу 105 (с. 88). Тогда мы решили её, применив теорему о пропорциональных отрезках. Здесь мы применим векторный подход и метод неопределенных коэффициентов.

Пусть ВА = а, ВС = b, АО = х ? AM, КО = у ? КС, тогда АО + ОК = АК, х ? АМ + (-у ? КС) = -1/2а.

Так как AM = AB + ВМ = – ВА + 3/4ВС = – а + 3/4b и КС = KB + ВС = -1/2ВА + ВС = -1/2а + b, то с учётом этого получаем уравнение: хAM + (-уКС) = -1/2а или х(-а + 3/4b) – у(-1/2а + b) = -1/2а. Приравнивая к нулю коэффициенты при векторах а и b, стоящих в левой и правой частях уравнения, получим систему:

х = 4/5, у = 3/5;

Итак,

значит,

Ответ: 3/10.

153. В выпуклом четырёхугольнике ABCD диагонали АС и BD пересекаются в точке F. Известно, что AF = CF = 2, BF = 1, DF = 4, ?BFC = ?/3.

Найти косинус угла между векторами АВ и DC (рис. 208). (3)

Рис. 208.

Решение:

Пусть ? – искомый угол между векторами АВ и DC тогда

Пользуясь свойствами скалярного произведения векторов и условиями задачи, вычислим АВ, DC и АВ ? DC. Так как

Теперь получаем, что

Ответ: 13/14.

Задачи для самостоятельного решения

154. Найдите геометрическое место точек, равноудалённых от данной прямой и данной точки. (2)

155. Продолжения сторон AD и ВС четырёхугольника ABCD пересекаются в точке Р. Точки М и N – середины сторон АВ и CD. Доказать, что если прямая MN проходит через точку Р, то ABCD – трапеция. (3)

156. Дан равнобедренный треугольник ABC, в котором проведены высота CD и перпендикуляр DE к боковой стороне ВС. Точка M – середина отрезка DE. Доказать, что отрезки АЕ и СМ перпендикулярны. (3)

157. Доказать, что для треугольника ABC и любой точки Р выполняется неравенство:

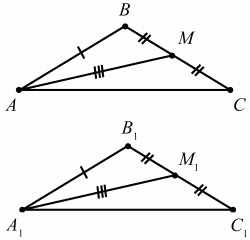
Разные задачи

Примеры решения задач

158. Можно ли утверждать, что треугольники равны по двум сторонам и медиане, проведенной к одной из этих сторон? Ответ: обоснуйте (рис. 209). (1)

Рис. 209.

Решение. Рассмотрим треугольники ABC и А1В1C1. Пусть AB = A1B1, BC = B1C1,AM = A1M1 (см. рис). Так как ВС = В1С1, то ВМ = В1М1 ?АВМ = ?A1B1M1 (по трём сторонам), значит, ?В = ?B1. В этом случае ?ABC = ?A1B1C1 по двум сторонам и углу между ними.

Ответ: да.

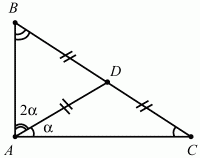
159. Определите острые углы прямоугольного треугольника, если медиана, проведённая к его гипотенузе, делит прямой угол в отношении 2:1 (рис. 210). (1)

Рис. 210.

Решение. Нарисуем треугольник ABC, где ?ВАС = 3? = 90°. Медиана AD равна длинам BD и CD, так как D – середина гипотенузы, а, значит, является центром описанной около треугольника окружности. Пусть для определённости ?BAD = 2?, ?DAC =?. Очевидно, что 2? + ? = 90°, ? = 30°. Учитывая, что треугольники BDA и DAC – равнобедренные, получаем:?В = 2? = 60°, ?С = ? = 30°.

Ответ: 60°, 30°.

160. Дан произвольный четырёхугольник ABCD. Точки М, N, Р, Q – середины его сторон. Докажите, что MNPQ – параллелограмм (рис. 211). (1)

Рис. 211.

Решение. Из условия задачи и чертежа видно, что MN – средняя средняя линия ?ABC и QP средняя линия ?ACD. Поэтому MN = 1/2АС и MN||AC; QP = 1/2АС и QP||АС. В итоге получаем, что MN = QP и MN||QP. Поэтому, по признаку параллелограмма четырёхугольник MNPQ – параллелограмм.

161. Диагонали АС и BD трапеции ABCD пересекаются в точке О. Докажите, что треугольник АОВ и COD имеют одинаковые площади (рис. 212). (2)

Рис. 212.

Решение. Обозначим через h высоту трапеции. Запишем равенства:

162. Стороны треугольника образуют арифметическую прогрессию. Доказать, что радиус окружности, вписанной в треугольник, равен 1/3 высоты, проведённой к средней по величине стороне треугольника. (3)

Решение. Пусть стороны а, b, с треугольника ABC образуют арифметическую прогрессию с разностью d. Будем считать, что а ? b ? с. тогда a = b – d, c = b + d, периметр Р = 2р = 3b.

Воспользуемся формулой r = S/P, получим r = 2S/3b. А так как S = 1/2bhb, то r = 1/3hb.

Задачи для самостоятельного решения

163. Диагонали трапеции делят её среднюю линию на три равные части. Как относятся основания этой трапеции? (1)

164. Докажите, что середины сторон равнобокой трапеции являются вершинами ромба. (1)

165. В параллелограмме, смежные стороны которого не равны, проведены биссектрисы четырех углов. Докажите, что при их пересечении образуется прямоугольник. (2)

166. Площадь четырёхугольника равна S. Найдите площадь параллелограмма, стороны которого равны и параллельны диагоналям четырёхугольника. (2)

167. Докажите, что в параллелограмме ABCD расстояния от любой точки диагонали АС до прямых ВС и CD обратно пропорциональны длинам этих сторон. (2)

168. В выпуклом четырёхугольнике длины диагоналей равны одному и двум метрам. Найти площадь четырёхугольника, зная, что длины отрезков, соединяющих середины его противоположных сторон, равны. (1)

Глава 3

Билеты по геометрии

Не нашли, что искали? Воспользуйтесь поиском по сайту: