Теоремы об углах. Углы в треугольнике. Вписанные в окружность углы

Свойство вертикальных углов.

Вертикальные углы равны (рис. 66):

? = ?.

Рис. 66.

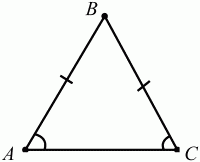
Свойство углов равнобедренного треугольника. В равнобедренном треугольнике углы при основании равны. Верна и обратная теорема: если в треугольнике два угла равны, то он равнобедренный (рис. 67):

АВ = ВС ? ?А = ?С.

Рис. 67.

Теорема о сумме углов в треугольнике.

Сумма внутренних углов треугольника равна 180° (рис. 68):

? + ? + ? = 180°.

Рис. 68.

Теорема о сумме углов в выпуклом n-угольнике.

Сумма углов выпуклого n-угольника равна 180°?(n – 2) (рис. 69).

Рис. 69.

Пример:?1 + ?2 + ?3 + ?4 + ?5 = 180°?(5–2) = 540°.

Теорема о внешнем угле треугольника.

Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним (рис. 70):

? = ? + ?.

Рис. 70.

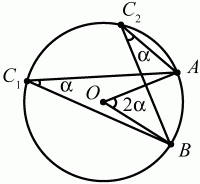
Теорема о величине вписанного в окружность угла.

Угол, вписанный в окружность, равен половине соответствующего q центрального угла (рис. 71):

Рис. 71.

Основные теоремы о треугольнике

Признаки равенства треугольников. Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны (рис. 72).

Рис. 72.

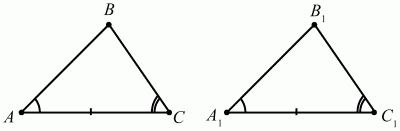
?ABC = ?A1B1C1 т. к. АB = А1В1, АС = А1С1 и ?A = ?A1.

Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны (рис. 73).

Рис. 73.

?ABC = ?A1B1C1 т. к. АC = А1C1, ?A = ?A1, ?C = ?C1.

Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны (рис. 74).

Рис. 74.

?ABC = ?A1B1C1 т. к. АB = А1B1, АC = А1C1, BC = B1C1.

Признаки равенства прямоугольных треугольников.

Если гипотенуза и катет одного треугольника соответственно равны гипотенузе и катету другого треугольника, то такие треугольники равны (рис. 75).

Рис. 75.

?ABC = ?A1B1C1 т. к. ?А = ?А1 = 90°; BC = B1C1; AB = A1B1.

Если гипотенуза и острый угол одного треугольника соответственно равны гипотенузе и острому углу другого треугольника, то такие треугольники равны (рис. 76).

Рис. 76.

?АВС = ?А1В1С1, т. к. АВ = А1В1, ?А = ?A1 a ?С = ?С1 = 90°.

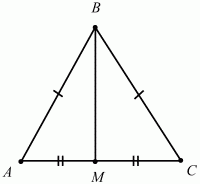
Свойство медианы равнобедренного треугольника.

В равнобедренном треугольнике медиана, проведённая к основанию, является биссектрисой и высотой (рис. 77).

Рис. 77.

(АВ = ВС, АМ = МС) ? (?АВМ = ?МВС, ?АМВ = ?ВМС = 90°).

Свойство средней линии треугольника.

Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна её половине (рис. 78).

Рис. 78.

EF||AC, EF = 1/2АС, т. к. АЕ = ЕВ и BF = FC.

Теорема синусов.

Стороны треугольника пропорциональны синусам противолежащих углов (рис. 79).

Рис. 79.

Теорема косинусов.

Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними (рис. 80).

Рис. 80.

а2= b2+ с2– 2bc cos ?.

Теорема Пифагора (частный случай теоремы косинусов).

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов (рис. 81).

Рис. 81.

с2= а2+ b2.

Пропорциональность и подобие на плоскости

Теорема Фалеса.

Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне (рис. 82).

Рис. 82.

(АВ = BC, AA1||BB1||CC1) ? A1B1 = В1С1, q и р – лучи, образующие угол ?.

а, b, с – прямые, пересекающие стороны угла.

Теорема о пропорциональных отрезках (обобщение теоремы Фалеса).

Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки (рис. 83).

Рис. 83.

или

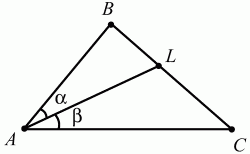
Свойство биссектрисы треугольника.

Биссектриса угла треугольника делит противолежащую ему сторону на отрезки, пропорциональные двум другим сторонам (рис. 84).

Рис. 84.

Если ? = ?, то

или

Признаки подобия треугольников.

Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны (рис. 85).

Рис. 85.

Треугольники ABC и A1B1C1 – подобные, т. к. ? = ?1 и ? = ?1.

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, и углы, образованные этими сторонами, равны, то треугольники подобны (рис. 86).

Рис. 86.

Треугольники ABC и A1B1C1 – подобны, т. к.

и ? = ?1.

Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны (рис. 87).

Рис. 87.

Треугольники ABC и A1B1C1 – подобны, т. к

Не нашли, что искали? Воспользуйтесь поиском по сайту: