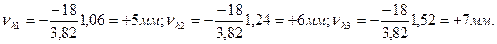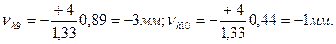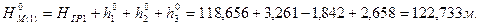|
|
Способ раздельного уравнивания140.1. Система полигонометрических ходов с одной узловой точкой
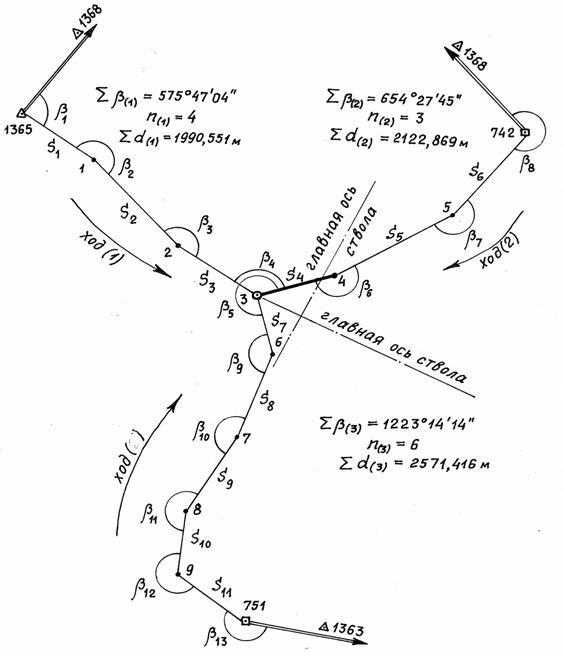
Задача. Сгущение геодезической сети для выполнения разбивочных работ на строительной площадке шахтного ствола. При рекогносцировке геодезической сети выявилось, что ближайшие исходные пункты находятся примерно в 2-х км от проектного центра шахтного ствола: № 1365 – пункт 2 класса, № 742 и № 751 – пункты 3 класса. Два пункта 2 класса, № 1368, видимый с пунктов № 1365 и № 742, и № 1363, видимый с пункта № 751, находятся на расстоянии примерно 12 и 8 км соответственно. На местности закреплены точки системы полигонометрических ходов 2 разряда с одной узловой точкой 3 и узловой линий 3-4 (рис. 14.10). Координаты исходных пунктов № 1365, № 742 и № 751 и дирекционные углы исходных направлений приведены в табл. 14.26. Значения измеренных углов и расстояний (горизонтальных проложений) приведены в табл 14.27. Решение задачи раздельного уравнивания производится с учетом весовых характеристик полигонометрических ходов: для дирекционных углов – число n углов в ходе; для координат – длина хода. 1. Вычисление вероятнейшего значения дирекционного угла узловой линии 3-4 по ходам (1), (2), (3). Дирекционный угол узловой линии вычисляется в данном случае трижды, по каждому полигонометрическому ходу, по формуле левых (см. рис. 14.10) горизонтальных углов:
Здесь следует иметь в виду, что при вычислении по ходу (2) дирекционный угол узловой линии получится обратным. Поэтому его необходимо будет изменить на 180о. Веса дирекционных углов определим для единицы веса ne = 4 (
Находим вероятнейшее значение дирекционных углов по формуле
Рис. 14.10. Система полигонометрических ходов с одной узловой точкой.
Таблица 14.26
Таблица 14.27
2. Уравнивание горизонтальных углов. Угловые невязки в каждом из полигонометрических ходов определяем, считая, что конечный дирекционный угол равен вероятнейшему значению дирекционного угла узловой линии. В соответствии с этим получим: fβ(1) = - 21" ; fβ(2) = + 6" ; fβ(3) = + 18" . Поправки в углы распределяем поровну. Таким образом, в углы хода (1) необходимо будет внести поправки по + 5" (а в один из углов - + 6"), в углы хода (2) – по - 2", хода (3) – по - 3". Значения уравненных горизонтальных углов приведены в табл. 14.28. Таблица 14.28
3. Вычисление вероятнейших значений координат узловой точки 3 по ходам (1), (2), (3). Координаты точки 3 в каждом из полигонометрических ходов определяем по формулам прямой геодезической задачи :
Вычисления с учетом уравненных значений горизонтальных углов приведены в табл. 14.29. Таблица 14.29
Примечание.Если длины сторон, образующих углы, заметно отличаются, то в горизонтальные углы, а затем и в дирекционные углы, можно вводить весовые поправки, предварительно определив веса углов. По ходам (1), (2) и (3) вычисляем значения приращений координат и координат узловой точки 3, используя для этого значения уравненных дирекционных углов. Неуравненные значения координат точек ходов приведены в ведомости в скобках. Определяем весовые характеристики ходов (1), (2), (3). В качестве единицы веса принимаем примерно среднюю длину хода (sе = 2000 м). Тогда
Находим вероятнейшие значения координат узловой точки 3 по формуле арифметической середины из результаов вычислений:
Получим Х3 = 20874,812 м ; Y3 = 9859,164 м. 1. Уравнивание координат точек полигонометрических ходов. Вычисляем значения невязок в координатах точки 3 по формулам
Полученные значения невязок в координатах приведены в табл. 14.29. На этом этапе расчётов необходимо убедиться в качестве выполненных полевых работ. Для этого вычисляют абсолютную и относительную невязки по каждому из ходов и сравнивают их с допустимой невязкой для принятого разряда геодезического построения. Вычисляем значения поправок в приращения координат по формулам
Полученные поправки выписаны в ведомость под значениями приращений координат. Вычисляем с учётом поправок уравненные значения координат точек ходов. Полученные уравненные значения координат записаны без скобок под предварительно вычисленными координатами. Качество решения задачи оценивается сходимостью координат узловой точки по всем ходам. Кроме того, как это требуется при обработке аналогичных систем, производят оценку точности по ходам по относительной погрешности хода. То есть необходимо вычислить абсолютную и относительную погрешности и проанализировать точность работ сравнением с допуском. Аналогично выполняется уравнивание систем полигонометрических ходов с двумя и более узловыми точками.
140.2. Система нивелирных ходов с одной узловой точкой
На рис. 14.11 представлена система нивелирных ходов с одной узловой точкой М. В табл. 14.30 приведены значения превышений, длины ходов между точками (в секциях), а также весовые характеристики ходов для sе = 3 км. Таблица 14.30
Рис. 14.11. Система нивелирных ходов с одной узловой точкой.
1. Трижды по ходам (1), (2) и (3) вычислить высоты узловой точки:
2. Установить единицу веса как примерно среднее арифметическое из длин ходов -
и вычислить веса ходов:
3. Вычислить арифметическую середину для высоты узловой точки по формуле
Для удобства следует определять её значение только для изменяемой части высоты:
4. Определить невязки в ходах по формуле
5. Вычислить поправки в превышения в ходах с учётом длин секций в ходе по формуле
где Ход (1): Ход (2): Ход (3): Контроль: сумма поправок в превышения хода должна быть равна невязке хода с обратным знаком. 6. Далее необходимо вычислить уравненные значения превышений в ходах с учётом полученных поправок и проконтролировать правильность уравнивания вычислением трижды значений уравненной высоты узловой точки. Эти значения должны совпасть. Возможны в данном случае незначительные отклонения до 1 мм, что обусловлено округлением результатов вычислений. Например, для хода (1): - уравненные значения превышений: h10 = +3256 + 5 = +3261 мм; h20 = - 1848 + 6 = - 1842 мм; h30 = + 2651 + 7 = + 2658 мм; - уравненное значение высоты узловой точки (по данному ходу):

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ;
; ;
; .
. ):
): ;
; 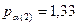 ;
;  .
.
 .
.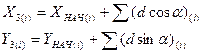 (14.160)
(14.160)

 .
. ;
;  (14.161)
(14.161)
 (14.162)
(14.162) ;
;  . (14.163)
. (14.163)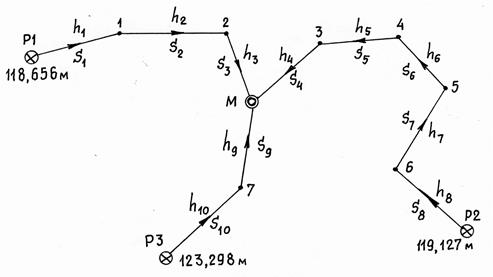
 ;
; ;
; .
. .
.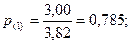
 ;
;  .
.
 .
. .
. : (14.164)
: (14.164)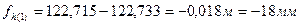 ;
; ;
; .
.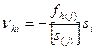 , (14.165)
, (14.165) - длина хода j ; si – длина секции iв ходе .
- длина хода j ; si – длина секции iв ходе .