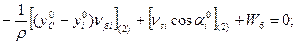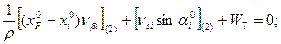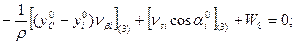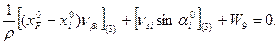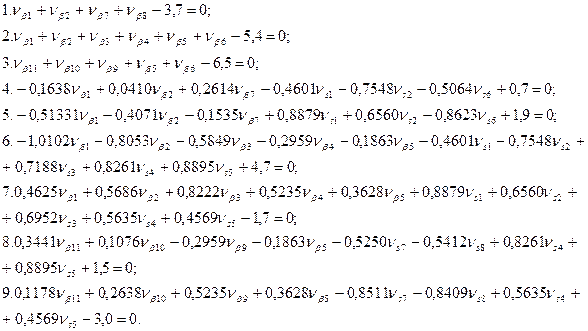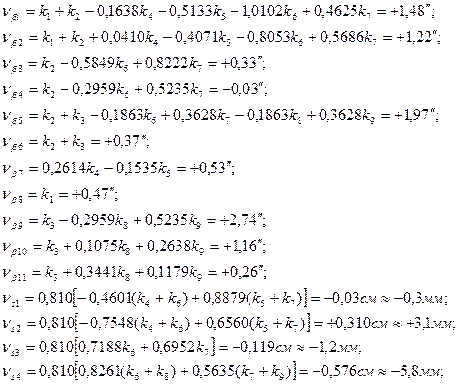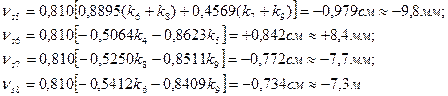|
|
Примеры коррелатного способа уравнивания
В этом разделе приводятся примеры уравнивания некоторых геодезических построений. В примерах рассматривается алгоритм решения задачи уравнивания для разных вариантов геодезических построений со сравнительно небольшим числом измеренных величин, как это часто имеет место, например, в практике геодезических и маркшейдерских работ на земной поверхности при создании опорных сетей либо в горных выработках при обработке результатов измерений в системах полигонометрических ходов. Уравнивание систем нивелирных ходов обычно производится при точных и высокоточных измерениях, например, при наблюдениях за деформациями горных выработок и наземных сооружений, что тоже имеет место и в практике геодезических и маркшейдерских работ. В примерах рассмотрены сравнительно простые схемы геодезических построений, однако принцип расчётов и в сложных системах точно такой же, как и в простых.
137.1. Уравнивание углов в полигоне
В полигоне, состоящем из четырёх вершин (рис. 14.7), неравноточно измерены горизонтальные углы: А = β1 , В = β2 , С = β3 , D = β4 (табл. 14.4). Выполнить уравнивание углов без учёта измерения длин сторон. Предварительно найдем веса pi и обратные веса qi, приняв
где s1 и s2 – стороны, образующие данный угол. Шаг 1. Общее число измеренных величин n = 4, число необходимых измерений k = 3, число избыточных измерений r = 1. Шаг 2. Составим условное уравнение (условие сумм углов полигона). β1' + β2' + β3' + β4' – 3600 = 0. Всего одно уравнение, поскольку r = 1. Шаг 3. Приводим условное уравнение к линейному виду, для чего продифференцируем его и найдем частные производные функции по аргументам βi . Очевидно, что а11 = +1, а21 = +1, а31 = +1, а41 = +1. Составим матрицу коэффициентов aij со строкой обратных весов qi (таблица 14.5).
Рис. 14.7. Уравнивание углов в полигоне.
Таблица 14.4 Исходные данные
Таблица 14.5 Матрица коэффициентов, весов и обратных весов
Свободный член уравнения W1 = [βi] – 3600 = 3600 00' 07,0" – 3600 = + 7". Шаг 4. Найдём коэффициенты bjj нормальных уравнений (в данном случае – уравнений коррелат):
т.е.
Для приведенного примера, с учётом значений aij и qi , 13,266 k1 + 7 = 0, откуда k1 = - 0,528. Шаг 5. Составляем условное уравнение поправок
и формулы для вычисления поправок (с вычислением их значений):
Контроль по формуле (14.94): условие выполнено! (проверьте сами). Отступление при округлениях значений поправок на 0,1" является допустимым. Вспомните загадку, которая прозвучала в начале этой главы. А если забыли, то возвратитесь к этому началу. Вот оно, что «под конец тонко» - это и есть хвостик решения всей задачи уравнивания: маленькие поправочки в измеренные величины. Ну а что тут было зелено, да посерёдке толсто – это уж понятно из решения данной задачи. Правда, приведенная задача – одна из самых простых. Дальше будет корнеплод посложнее. Но, всему своё время. А сейчас – закончим решение приведенной задачи. Шаг 6. Вычисляем уравненные значения углов: β1' = 80° 16' 44,3" – 2,4" = 80° 16' 41,9"; β2' = 91° 45' 00,7" – 1,1" = 91° 44' 59,6"; β3' = 69° 25' 56,8" – 1,2" = 69° 25' 55,6"; β4' = 118° 32' 25,2" – 2,4" = 181° 32' 22,8". Контроль: подстановка уравненных значений углов в уравнение (14.91) – условие выполнено! (проверьте это условие). Очевидно, что при равноточных измерениях углов для них были бы получены одинаковые поправки, т.е. невязка была бы распределена поровну во все углы.
137.2. Уравнивание системы нивелирных ходов с несколькими узловыми точками
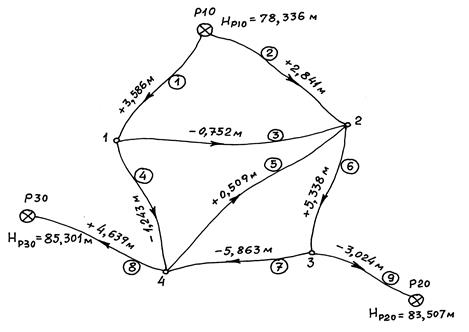
На местности пройдена система нивелирных ходов с четырьмя узловыми точками 1, 2, 3 и 4 (рис. 14.8). В результате измерений образовано 9 секций, превышения в которых по указанному направлению приведены непосредственно на схеме. Указаны также высоты исходных реперов Р10, Р20 и Р30. В табл. 14.6 приведены длины ходов в секциях и значения весов и обратных весов превышений в секциях, вычисленные по формулам:
Рис. 14.8. Схема нивелирных ходов с четырьмя узловыми точками. Таблица 14.6 Исходные данные
se = 2 км
где Требуется определить уравненные значения высот узловых точек. Шаг 1. Общее число измерений n = 9, число необходимых измерений k = 4, число избыточных измерений r = 5. Шаг 2. Составим r = 5 условных уравнений: 1. h1' + h3' – h2' = 0 2. h4' + h5' – h3' = 0 3.h6' + h7' + h5' = 0 (14.96) 4. h7' + h8' – h9' – (HP30 – HP20) = 0 5. h1' + h4' + h8' – (HP30 – HP10) = 0 Шаг 3. Приведём условные уравнения к линейному виду, продифференцировав их по аргументам hi. Получим коэффициенты aij условных уравнений поправок: а11 = +1 ; а31 = +1; а21 = - 1 ; а42 = +1 ; а52 = +1 ; а32 = - 1 ; а63 = +1 ; а73 = +1 ; а53 = +1 ; а74 = +1 ; а84 = +1 ; а94 = - 1 ; а15 = +1 ; а45 = +1 ; а85 = +1 . Составим матрицу коэффициентов aij со строкой обратных весов qi (табл. 14.7). Таблица 14.7 Матрица коэффициентов и обратных весов
Вычислим свободные члены (в мм), подставив в уравнения (14.96) измеренные значения hi в секциях: W1 = h1 + h3 – h2 = 3586 – 752 – 2841 = - 7 мм; W2 = h4 + h5 – h3 = -1243 + 509 – (-752) = +18 мм; W3 = h6 + h7 + h5 = 5338 – 5863 + 509 = - 16 мм; W4 = h7 + h8 – h9 – (HP30 – HP20) = - 5863 + 4639 – (-3024) – 1794 = +6 мм; W5 = h1 + h4 + h8 – (HP30 – HP10) = 3586 – 1243 + 4639 – 6965 = +17 мм. Шаг 4. Найдём по формулам (14.88) коэффициенты bjj нормальных уравнений коррелат:
После подстановки значений aij и qi в уравнения (14.97) получим исходные нормальные уравнения коррелат: 1. 2,18k1 – 1,08 k2 + 0,42 k5 – 7 = 0; 2. -1,08 k1 + 2,79 k2 + 1,32 k3 + 0,39 k5 + 18 = 0; 3. 1,32 k2 + 3,86 k3 + 1,51 k4 – 16 = 0; (14.98) 4. 1,51 k3 + 4,42 k4 + 1,72 k5 + 6 = 0; 5. 0,42 k1 + 0,39 k2 + 1,72 k4 + 2,53 k5 + 17 = 0. Из решения системы уравнений (14.98) одним из способов получим: k1 = - 2,137; k2 = - 11,552; k3 = +9,606; k4 = -3,882; k5 = -1,945. Контроль вычисления коррелат выполняем подстановкой их значений в исходные уравнения (14.98): 1. 2,18 (-2,137) – 1,08 (-11,552) + 0,42 (-1,945) – 7 = + 0,001; 2. -1,08(-2,137) + 2,79(-11,552) + 1,32(+9,606) + 0,39(-1,945) + 18 = -0,001; 3. 1,32(-11,552) + 3,86(+9,606) + 1,51(-3,882) – 16 = - 0,031; 4. 1,51(+9,606) + 4,42(-3,882) + 1,72(-1,945) + 6 = +0,001; 5. 0,42(-2,137) + 0,39(-11,552) + 1,72(-3,882) + 2,53(-1,945) + 17 = -0,001. Сравнительно большее невыполнение условия мы видим в уравнении 3. Это вызвано погрешностями округлений. При вычислении с большими значащими цифрами этого не наблюдалось бы. При этом результаты вычислений принимаем удовлетворительными, поскольку поправки в измеренные значения превышений для данных условий будут в дальнейшем округляться до 1 мм, а вычисления проведены с большим запасом точности. Шаг 5. Составляем условные уравнения поправок vi, пользуясь формулами (14.86) и табл. 14.7:
После подстановки значений qi, aij и kj в (14.99) получим: 1. v1 = 0,42 ∙1∙ (-2,137) + 0,42∙1∙ (-1,945) = - 1,714 = - 2 мм; 2. v2 = 0,68 ∙ (-1) ∙ (-2,137) = + 1,453 = + 1 мм; 3. v3 = 1,08 ∙ 1 ∙ (2,137) + 1,08 ∙ (-1) ∙ (-11,552) = +10,168 = + 10 мм; 4. v4 = 0,39 ∙ 1 ∙ (-11,552) + 0,39 ∙1 ∙ (-1,945) = - 5,264 = - 5 мм; 5. v5 = 1,32 ∙1∙ (-11,552) + 1,32 ∙ 1 ∙ (+9,606) = - 2,569 = - 3 мм; 6. v6 = 1,03 ∙1 ∙ (+9,606) = + 9,894 = + 10 мм; 7. v7 = 1,51 ∙ 1 ∙ (+9,606) + 1,51 ∙1 ∙ (-3,882) = + 8,643 = + 9 мм; 8. v8 = 1,72 ∙ 1 ∙ (-3,882) + 1,72 ∙ 1 ∙ (-1,945) = - 10,022 = - 10 мм; 9. v9 = 1,19 ∙ (-1) ∙ (-3,882) = + 4,620 = + 5 мм. Контроль вычисления поправок можно выполнить по формулам (14.96), подставив в них вместо превышений значения поправок (суммы поправок должны быть равны значениям соответствующих невязок с обратным знаком): 1. v1 + v3 – v2 = - 2 + 10 – 1 = + 7 мм (= - W1); 2. v4 + v5 – v3 = - 5 – 3 – 10 = - 18 мм (= - W2 ); 3. v6 + v7 + v5 = +10 + 9 – 3 = + 16 мм (= - W3 ); 4. v7 + v8 – v9 = + 9 – 10 – 5 = - 6 мм (= - W4 ); 5. v1 + v4 + v8 = - 2 – 5 – 10 = - 17 мм (= - W5 ). Шаг 6. Вычисляем уравненные значения превышений в секциях и контролируем уравнивание по выполнению условия (14.96): h1'= + 3586 – 2 = + 3584 мм; h2'= + 2841 + 1 = + 2842 мм; h3'= - 752 + 10 = - 742 мм; h4 '= - 1243 – 5 = - 1248 мм; h5'= + 509 – 3 = + 506 мм; h6 '= + 5338 + 10 = + 5348 мм; h7'= - 5863 + 9 = - 5854 мм; h8'= + 4639 – 10 = + 4629 мм; h9 '= - 3024 + 5 = - 3019 мм. Подстановка в уравнения (14.96) подтверждает выполнение указанного условия. Вычисляем уравненные значения высот узловых точек 1, 2 , 3 и 4: Н1 = НР10 + h1' = 78,336 + 3,584 = 81,920 м; H2 = HP10 + h2' = 78,336 + 2,842 = 81,178 м; H3 = HP20 – h9' = 83,507 – (- 3,019) = 86,526 м; H4 = HP30 – h8' = 85,301 – 4,629 = 80,672 м. Контроль вычислений здесь можно выполнить вторичным получением высот искомых точек по другим направлениям. Должны получиться те же результаты. Например, H1 = HP30 – h8' – h4' = 85,301 – 4,629 + 1,248 = 81,920 м. Задача решена.
137.3. Уравнивание системы полигонометрических ходов с двумя узловыми точками
Уравнивание таких систем полигонометрических ходов аналогично уравниванию как одиночного полигонометрического хода, так и системы полигонометрических ходов с одной узловой точкой. В такой системе (рис. 14.9) образуется три независимых полигонометрических хода [(1), (2), (3)], в которых возникает по три условия: три условия дирекционных углов и шесть условий координат, т.е. получается девять условных уравнений.
Рис. 14.9. Система полигонометрических ходов с двумя узловыми точками.
В табл. 14.8, 14.9 и 14.10 приведены необходимые исходные данные для решения задачи уравнивания, заключающейся в определении уравненных значений координат точек 1, 2, 3, M, N, а также уравненного значения дирекционного угла узловой линии MN. (В данном примере узловые точки M и N образуют и узловую линию). Часто между узловыми точками прокладывают полигонометрический ход в две и более линии. Тогда понятие узловой линии не будет иметь места. Ею может быть любая линия с началом в какой-либо узловой точке). Горизонтальные углы измерены равноточно с погрешностью mβ = 2,0". Расстояния измерены светодальномером с погрешностью, примерно одинаковой для всех линий (ms = 18 мм = 1,8 см). В соответствии с указанной точностью измерения расстояний и углов веса углов принимаем равными единице (pβ = 1; qβ = 1), а веса расстояний –
Таблица 14.8 Координаты исходных пунктов
Таблица 14.9 Исходные дирекционные углы
Таблица 14.10 Измеренные горизонтальные углы и расстояния
Выполним предварительные вычисления в полигонометрических ходах (1), (2) и (3), т.е. определим координаты точек ходов, используя только измеренные величины (табл. 14.11). Шаг 1. Общее число измерений n = 19 (11 углов и 8 расстояний), число необходимых измерений k = 10, число избыточных измерений r = 9.
Таблица 14.11 Ведомость координат
Шаг 2. Составление условных уравнений. Для трёх независимых ходов, будем иметь три условных уравнения для дирекционных углов и шесть условных уравнений для координат ( три – для абсцисс, три – для ординат). 1. 2. 3. 4. 5. 6. 7. 8. 9. В уравнениях (14.100) индексы (1), (2) и (3) относятся к соответствующим ходам (см. табл. 14.11), например, n(1) = 4, n(2) = 6, n(3) = 5. Приведём условные уравнения к линейному виду по правилам, изложенным выше. В полученные выражения введём знак гауссовых сумм. 1. 2. 3. 4. 5. 6. 7. 8. 9. В уравнениях (14.101) значения координат берут в километрах, а значение ρ = 206265″ уменьшают на 100000. Вычислим значения невязок в уравнениях (14.101) с учётом данных измерений и предварительных вычислений: Wi = Tio – Ti(исх) , (14.102) где Tio – результат вычисления исходной величины Ti(исх). W1 = 144º 21' 14,3" – 144º 21' 18,0" = - 3,7" ; W2 = 118º 19' 09,3" – 118º 19' 14,7" = - 5,4" ; W3 = 118º 19' 08,2" – 118º 19' 14,7" = - 6,5" ; W4 = 6124,931 – 6124,924 = +0,007 м = + 0,7 см; W5 = 4718,067 – 4718,048 = + 0,019 м = + 1,9 см; W6 = 8137,612 – 8137,565 = + 0,047м = + 4,7 см; W7 = 6463,765 – 6463,782 = - 0,017 м = - 1,7 см; W8 = 8137,580 – 8137,565 = + 0,015 м = + 1,5 см; W9 = 6463,752 – 6463,782 = - 0,030 м = - 3.0 см . По данным табл. 14.11 составим табл. 14.12 значений синусов и косинусов дирекционных углов и разностей абсцисс и ординат. Получим окончательные условные уравнения поправок: Таблица 14.12 Значения синусов и косинусов дирекционных углов, значения разностей координат
(14.103) Составим матрицу коэффициентов aij и обратных весов qi , необходимую для определения коэффициентов нормальных уравнений коррелат (табл. 14.13). Таблица 14.13 Матрица коэффициентов и обратных весов
(продолжение табл. 14.13)
Шаг 4. Составление нормальных уравнений коррелат. 1. 4k1 + 2 k2 + 0,1386 k4 – 1,0739 k5 – 1,8155 k6 + 1,0311 k7 – 3,7= 0; 2. 2 k1 + 6 k2 + 2 k3 – 0,1228 k4 – 0,9204 k5 – 2,8827 k6 + 2,7396 k7 - 0,1863 k8 + +0,3628 k9 – 5,4 = 0; 3. 2 k2 + 5 k3 – 0,1863 k6 +0,3628 k7 -0,0306 k8 + 1,2679 k9 – 6,5 = 0; 4. 0,1386 k1 – 0,1228 k2 + 0,9375 k4 -0,3510 k5 +0,7654k6 – 0,7844 k7 + 0,7 = 0; 5. -1,0739 k1 – 0,9204 k2 – 0,3510 k4 + 2,3327 k5 + 0,1144 k6 + 0,5182 k7 + 1,9 = 0; 6. -1,8155 k1 – 2,8827 k2 – 0,1863 k3 + 0,7654 k4 + 0,1144 k5 + 4,3786 k6 -1,2495 k7 + + 1,2284 k8 + 0,6387 k9 + 4,7 = 0; 7. 1,0311 k1 + 2,7396 k2 + 0,3628 k3 – 0,7844 k4 +0,5182k5 -1,2495 k6 + 3,4238 k7 + +0,6387 k8 + 0,5579 k9 – 1,7 = 0; 8. -0,1863 k2 – 0,0306 k3 + 1,2284 k6 + 0,6387 k7 + 1,9065 k8 + 1,2832 k9 + 1,5 = 0; 9. 0,3628 k2 + 1,2679 k3 + 0,6387 k6 + 0,5579 k7 + 1,2832 k8 + 2,0749 k9 – 3,0 = 0. (14.104) Из решения системы нормальных линейных уравнений (14.104) получим: k1 = + 0,474; k2 = - 0,375; k3 = + 0,740; k4 = - 0,379; k5 = - 0,983; k6 = - 0,614; k7 = + 0,422; k8 = - 2,263; k9 = + 2,534. Подстановка полученных значений коррелат в исходные уравнения (14.104) показывает выполнение указанных условий. Шаг 5. Составление уравнений поправок и вычисление поправок. В соответствии с таблицей 14.13: Таблица 14.14 Ведомость координат
Шаг 6. Вычисление уравненных значений координат и дирекционных углов. Поправки в измеренные величины вводим непосредственно при обработке ведомости уравнивания (табл. 14.14), составленной по аналогии с табл. 14.12. Как видно из данных уравнивания (при сравнении с исходными даными) линейные остаточные невязки в ходах не превышают 3-х мм, угловые остаточные невязки равны нулю. Задача решена. Остаточные невязки в углах и координатах являются несущественными и зависят от округления промежуточных результатов. Обычно после завершения уравнивания значения координат округляют до 1 мм, а значения углов до 0,1".

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
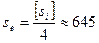 м (см. табл. 14.4) без учёта величин измеренных углов, считая их практически примерно одинаковыми (значения весов определяются по условию возможной погрешности в направлениях из-за центрирования теодолита; для веса угла применяется правило сложения обратных весов направлений):
м (см. табл. 14.4) без учёта величин измеренных углов, считая их практически примерно одинаковыми (значения весов определяются по условию возможной погрешности в направлениях из-за центрирования теодолита; для веса угла применяется правило сложения обратных весов направлений):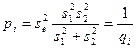 , (14.91)
, (14.91)
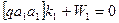 , (14.92)
, (14.92) . (14.93)
. (14.93)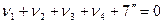 (14.94)
(14.94)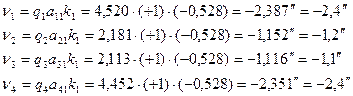
 , (14.95)
, (14.95)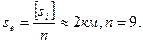
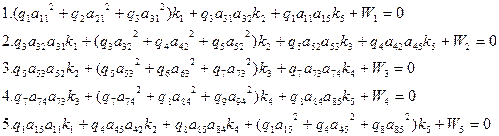 (14.97)
(14.97)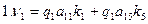
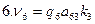
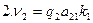
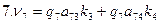 (14.99)
(14.99)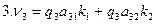
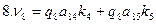

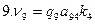
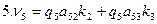

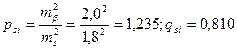
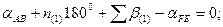
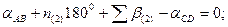
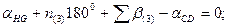
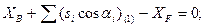
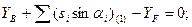 (14.100)
(14.100)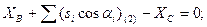
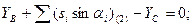
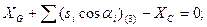
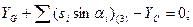
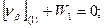
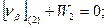
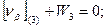
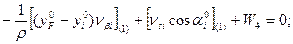
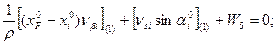 (14.101)
(14.101)